
Задачник по физике
.pdf
36.
37.
38.
39.
40.
41.
42.
43.
44.
V = 5 л под давлением p = 500 кПа. |
|
|
|
|
|
i = 6 ) |
|
||||
Некоторый |
трехатомный |
газ |
(количество |
степеней |
свободы |
под |
|||||
давлением |
p = 202 |
кПа и |
температуре |
t = 27oC |
занимает объем |
||||||
V =10 л. |
Определить |
теплоемкость |
С′р |
этого |
газа |
при |
постоянном |
||||
давлении. |
|
|
|
|
|
|
|
|
|
i = 6 ) |
|
Некоторый |
трехатомный |
газ |
(количество |
степеней |
свободы |
под |
|||||
давлением |
p = 202 |
кПа и |
температуре |
t = 27oC |
занимает объем |
||||||
V =10 л. |
Определить |
теплоемкость |
СV′ |
этого |
газа |
при |
постоянном |
||||
объеме. |
|
|
|
|
|
|
степеней свободы i = 5) в |
||||
Идеальный |
двухатомный |
газ |
(количество |
|
|||||||
количестве ν = 3 моль, занимающий объем V1 = 10 л и находящийся под |
|||||||||||
давлением |
p1 = 1 |
МПа, |
подвергли |
изохорному |
нагреванию |
до |
|||||
температуры T2 = 500 |
К. |
Затем |
газ |
|
подвергли |
изотермическому |
|||||
расширению до начального давления, а после этого в результате изобарного сжатия газ был возвращен в первоначальное состояние. Определить термический коэффициент полезного действия η .
Идеальный газ, рабочее тело теплового двигателя, совершает замкнутый цикл, состоящий из последовательности процессов: изобарного, адиабатного и изотермического. Известно, что в результате изобарного
процесса газ нагревается от Т1 = 300 К до Т2 = 700 К. Определить термический коэффициент полезного действия η .
При нагревании двухатомного идеального газа (количество степеней свободы i = 5 ) в количестве ν = 3 моль его термодинамическая температура увеличилась в θ = 2 раза. Определить изменение энтропии S , если нагревание происходило изохорно.
При нагревании двухатомного идеального газа (количество степеней свободы i = 5 ) в количестве ν = 3 моль его термодинамическая температура увеличилась в θ = 2 раза. Определить изменение энтропии S , если нагревание происходило изобарно.
Идеальный газ (количество степеней свободы
моль сначала изобарно нагрели, так что объем газа увеличился в θ = 2 раза, затем изохорно охладили, в результате чего давление его уменьшилось в β = 3 раза. Определить изменение энтропии S в ходе
указанных процессов.
Во сколько раз θ необходимо увеличить объем идеального газа в количестве ν = 3 моль при изотермическом расширении, чтобы произошло приращение энтропии на величину S =100 Дж/К?
При адиабатном сжатии давление воздуха (количество степеней свободы i = 5) было увеличено от р1 =100 кПа до р2 = 500 кПа. Затем при неизменном объеме температура газа была понижена до первоначальной.
- 61 -
Определить давление р3 воздуха в конце процесса.
45. Имеются три сосуда вместимостью V1 = 3 л, V2 = 6 л и V3 = 9 л, в которых находятся идеальные газы под давлениями p1 =101 Па, p2 = 202 Па и p3 = 303 Па. Под каким давлением p окажется смесь
газов, если эти сосуды мгновенно соединить между собой? Считать, что процесс смешения газов идет адиабатически, а коэффициент адиабаты принять равным γ = 1,4.
***** §9 *****
§10. Контрольные задачи по теме7 «Свободныенезатухающиеколебанияиупругиеволны.
Специальнаятеорияотносительности»
1. |
Математический маятник длиной L = 1 м начинают отслеживать (включают |
||||||||||||
|
секундомер) в тот момент, когда он отклонился на угол, равный половине от |
||||||||||||
|
максимального |
(ϕ = 1 2ϕ0 ). |
Через |
какой минимальный |
промежуток |
||||||||
|
времени T |
после |
начала |
отсчета времени |
маятник |
пройдет |
через |
||||||
|
положение равновесия? |
|
|
|
|
|
|
|
|
|
|||
2. |
За математическим |
маятником |
длиной |
L = 1 |
м начинают |
наблюдать |
|||||||
|
(включают секундомер) в тот момент, когда он отклонился на угол, равный |
||||||||||||
|
половине |
от |
максимального |
|
(ϕ1 = 1 2ϕ0 ). |
|
Найти |
скорость υ |
|||||
|
математического маятника в момент прохождения им положения |
||||||||||||
|
равновесия, если амплитуда у такого маятника ϕ0 = 6o. |
|
|
|
|||||||||
3. |
За математическим |
маятником |
длиной |
L = 1 |
м начинают |
наблюдать |
|||||||
|
(включают секундомер) в тот момент, когда он отклонился на угол, равный |
||||||||||||
|
половине |
от |
максимального |
(ϕ1 = 1 2ϕ0 ). |
Найти |
величину |
|||||||
|
тангенциального |
ускорения |
aτ |
|
математического |
маятника |
в |
момент |
|||||
прохождения им положения ϕ2 =  2 2ϕ0 , если амплитуда у такого маятника ϕ0 = 6o.
2 2ϕ0 , если амплитуда у такого маятника ϕ0 = 6o.
4. Пружинный маятник (груз массы m = 2 кг прикреплен к абсолютно упругой пружине жесткостью k = 8 Н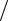 м и приведен в колебательное движение на
м и приведен в колебательное движение на
гладком столе) начинают отслеживать (включают секундомер) в тот момент, когда он прошел расстояние, равное половине от максимального
7 Контрольные задачи задания №3
- 62 -
5.
6.
7.
8.
9.
10.
11.
12.
( x = 1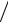 2x0 ). Через какой минимальный промежуток времени T после
2x0 ). Через какой минимальный промежуток времени T после
начала отсчета времени маятник пройдет через положение равновесия? Определить отношение кинетической энергии математического маятника к его потенциальной энергии θ в момент времени T = 2 c после включения секундомера, если длина маятника составляет L = 1 м и начальная фаза
α0 = π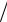 4 .
4 .
Определить полную энергию W пружинного маятника в момент времени T = 2 c после включения секундомера, если его собственная частота колебаний составляет ω = 4 рад/с, масса m = 2 кг, начальная фаза α0 = π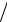 4 и амплитуда x0 = 0,2 м.
4 и амплитуда x0 = 0,2 м.
За математическим маятником длиной L = 1 м начинают наблюдать (включают секундомер) в тот момент, когда он отклонился на угол, равный
половине |
от |
максимального |
(ϕ = 1 2ϕ0 ). |
Найти модуль полного |
|
ускорения |
a |
такого маятника |
в момент прохождения им |
положения |
|
ϕ = 2 2ϕ0 , если амплитуда у такого маятника ϕ0 = 6o. |
|
||||
За математическим маятником |
длиной L = 1 |
м начинают |
наблюдать |
||
(включают секундомер) в тот момент, когда он отклонился на угол, равный
половине от максимального (ϕ1 = 1 2ϕ0 ). Найти острый угол β , |
который |
|||||||||||||||||
вектор полного |
ускорения |
|
|
a математического |
маятника составляет |
с |
||||||||||||
вертикалью в момент прохождения им положения ϕ2 = |
2 2ϕ0 . |
|
|
|
||||||||||||||
Система Σ′ |
движется относительно системы |
Σ со скоростью υ = 0,6c |
||||||||||||||||
( c −скорость |
света) |
так, |
|
′ |
что |
|
координатные |
оси |
систем |
попарно |
||||||||
параллельны. В системе |
Σ |
|
|
|
|
|
|
|
′ |
′ |
′ |
и |
||||||
|
|
стержень покоится в плоскости Z O X |
||||||||||||||||
ориентирован под углом α |
′ |
= |
o |
|
|
′ |
′ |
|
|
|
|
|
||||||
|
30 |
к оси O X |
. Определить длину стержня |
|||||||||||||||
L в системе Σ, если собственная длина стержня в системе Σ′ равна |
||||||||||||||||||
L0 = 2м. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Система Σ′ |
движется относительно системы |
Σ со скоростью υ = 0,6c |
||||||||||||||||
( c −скорость |
света) |
так, |
|
′ |
что |
|
координатные |
оси |
систем |
попарно |
||||||||
параллельны. В системе |
Σ |
|
|
|
|
|
|
|
′ |
′ |
′ |
и |
||||||
|
′ |
стержень покоится в плоскости Z O X |
||||||||||||||||
ориентирован |
под |
углом |
α |
= 30 |
o |
к оси |
|
′ |
′ |
|
угол |
|
α |
|||||
|
|
O X . Определить |
|
|||||||||||||||
ориентации стержня в системе Σ.
Пружинный маятник (груз массы m = 2 кг прикреплен к абсолютно упругой пружине жесткостью k = 8 Н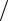 м и приведен в колебательное движение на гладком столе) начинают отслеживать (включают секундомер) в тот момент,
м и приведен в колебательное движение на гладком столе) начинают отслеживать (включают секундомер) в тот момент,
когда он прошел расстояние, равное половине |
от максимального |
||||
( x1 = 1 2x0 ). |
Найти величину |
ускорения |
a |
маятника в |
момент |
прохождения им |
положения x2 = |
2 2x0 , |
если |
амплитуда у |
такого |
маятника x0 = 20см.
Пружинный маятник (груз массы m = 2 кг прикреплен к абсолютно упругой
- 63 -

пружине жесткостью k = 8 Н м и приведен в колебательное движение на
м и приведен в колебательное движение на
гладком столе) начинают отслеживать (включают секундомер) в тот момент, когда он прошел расстояние, равное половине от максимального
|
( x1 = 1 2x0 ). |
Найти |
величину |
|
|
скорости |
|
υ |
|
маятника |
в |
|
момент |
||||||||
|
прохождения |
им |
положения |
x2 = |
|
2 2x0 , |
если |
амплитуда |
у |
такого |
|||||||||||
|
маятника x0 = 20см. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
13. |
Физический |
маятник представляет |
собой |
тонкий |
однородный |
стержень |
|||||||||||||||
|
длиной L = 1 м. Определить, на каком расстоянии S от центра масс |
||||||||||||||||||||
|
должна располагаться точка подвеса такого маятника, чтобы частота его |
||||||||||||||||||||
|
колебаний была максимальной (ω = ωмах). |
|
|
|
|
|
|
|
|
|
|
||||||||||
14. |
Определить отношение θ кинетической энергии |
линейного осциллятора к |
|||||||||||||||||||
|
его потенциальной энергии |
в момент времени T = 2 c после включения |
|||||||||||||||||||
|
секундомера, |
если коэффициент |
жесткости такого |
маятника |
составляет |
||||||||||||||||
|
k = 8 Н/м, |
|
масса m = 2 кг, и начальная фаза α0 = π 4 . |
|
|
|
|
|
|||||||||||||
15. |
Система Σ′ |
|
движется относительно системы |
Σ со скоростью υ = 0,6c |
|||||||||||||||||
|
( c −скорость |
света) так, что координатные |
оси |
систем |
попарно |
||||||||||||||||
|
параллельны. В системе |
Σ |
релятивистская частица движется со скоростью |
||||||||||||||||||
|
u = 0,8c |
в |
плоскости |
|
′ |
′ |
′ |
|
под |
углом |
|
|
|
o |
к |
оси |
OX. |
||||
|
Z O X |
|
α = 30 |
||||||||||||||||||
|
Определить соответствующий угол α |
′ |
|
|
|
′ |
|
|
|
|
|
|
|
||||||||
|
|
в системе Σ . |
|
|
|
|
|
|
|
||||||||||||
16. |
Релятивистская частица массой покоя |
m = 10−28кг |
|
движется |
|||||||||||||||||
|
прямолинейно, испытывая действие постоянной |
силы |
F = 105 H . |
||||||||||||||||||
|
Определить |
|
скорость частицы υ |
|
в момент |
времени |
T = 10 c |
|
после |
||||||||||||
|
включения секундомера, если в начальный момент времени ее скорость |
||||||||||||||||||||
|
υ0 = 0м с. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17. |
Кинетическая энергия неизвестной частицы оказалась равной ее энергии |
||||||||||||||||||||
|
покоя (Wk =W0 ). Определить скорость υ такой частицы. |
|
|
|
|
|
|||||||||||||||
18. |
Продольные |
размеры электрона |
уменьшились |
в |
θ = 2 |
раза |
|
в |
поле |
||||||||||||
|
плоского конденсатора, |
расстояние |
|
между обкладками |
которого |
|
равно |
||||||||||||||
|
d = 10 см. Действие какого электростатического поля E испытал на себе |
||||||||||||||||||||
|
электрон? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
19. |
Определить, |
какую ускоряющую разность потенциалов U должен пройти |
|||||||||||||||||||
|
электрон, чтобы его скорость составила θ = 90% скорости света? |
|
|
||||||||||||||||||
20. |
Определить работу A, которую надо совершить, |
чтобы увеличить скорость |
|||||||||||||||||||
|
от υ1 = 0,5c до υ2 = 0,7c ( с −скорость света) |
релятивистской частицы |
|||||||||||||||||||
|
массой m = 10−10г. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
21. |
Пружинный маятник, обладающий жесткостью |
|
k = 900 Н/м и |
массой |
|||||||||||||||||
|
M = 4 кг, |
|
смонтирован на гладком столе. |
|
Пуля массой |
m = |
10 г, |
||||||||||||||
|
летящая параллельно поверхности стола со |
скоростью |
υ0 = 600 м/c , |
||||||||||||||||||
|
попадает в центр масс маятника и застревает в нем. Определить амплитуду |
||||||||||||||||||||
- 64 -

колебаний x0 образовавшегося маятника и написать закон x = x(t ) его
колебаний. Сопротивлением воздуха и массой пружины пренебречь. Секундомер включают одновременно с попаданием пули в маятник.
22. Пружинный маятник, обладающий жесткостью k = 900 Н/м и массой M = 4 кг, смонтирован на гладком столе. Пуля массой m = 10 г,
летящая параллельно поверхности стола со скоростью υ0 = 600 м/c ,
|
попадает в центр масс маятника и застревает в нем. Определить частоту |
||||||
|
собственных колебаний ω0 образовавшегося маятника и написать закон |
||||||
|
x = x(t ) его колебаний. Сопротивлением воздуха и массой пружины |
||||||
|
пренебречь. Секундомер включают одновременно с попаданием пули в |
||||||
|
маятник. |
|
|
k = 900 Н/м и массой |
|||
23. |
Пружинный |
маятник, обладающий жесткостью |
|||||
|
M = 4 кг, |
смонтирован на гладком столе. |
Пуля массой |
m = 10 г, |
|||
|
летящая параллельно поверхности стола со |
скоростью |
υ0 = 600 м/c , |
||||
|
попадает |
в |
центр масс маятника и застревает |
в нем. |
Написать закон |
||
|
υ =υ(t) |
изменения скорости образовавшегося |
маятника |
от времени. |
|||
Сопротивлением воздуха и массой пружины пренебречь. Секундомер включают одновременно с попаданием пули в маятник.
24. Пружинный маятник, обладающий жесткостью k = 900 Н/м и массой M = 4 кг, смонтирован на гладком столе. Пуля массой m = 10 г,
летящая параллельно поверхности стола со скоростью υ0 = 600 м/c ,
попадает |
в центр масс маятника и застревает в нем. Написать закон |
a = a(t) |
изменения ускорения образовавшегося маятника от времени. |
Сопротивлением воздуха и массой пружины пренебречь. Секундомер включают одновременно с попаданием пули в маятник.
25Тонкий однородный стержень длиной L = 1 м может свободно вращаться вокруг горизонтальной оси, отстоящей на расстоянии S = 40 см от его середины. Определить период T колебаний стержня. если он совершает малые колебания.
26Однородный диск радиусом R = 20 cм совершает малые колебания около
=10 см от
|
геометрического центра диска. Определить собственную частоту ω |
||||
|
свободных колебаний диска относительно этой оси. |
|
|||
27 |
Два математических маятника колеблются с одинаковой угловой амплитудой |
||||
|
согласно уравнению ϕi |
= ϕ0 cosωit ( i = 1,2), но первый маятник имеет |
|||
|
в q = 2 раза большую длину. Определить отношение θ кинетической |
||||
|
энергии первого маятника к кинетической энергии второго маятника в |
||||
|
сходственных точках колебательного процесса, то есть при отклонениях от |
||||
|
положения равновесия на одинаковый угол. |
|
|
||
28 |
Два математических маятника колеблются с одинаковой угловой |
||||
|
амплитудой, |
но первый |
маятник имеет в |
q = 2 раза большую |
длину. |
|
Определить |
отношение |
θ полной энергии |
первого маятника к |
полной |
- 65 -
энергии второго маятника в сходственных точках колебательного процесса, то есть при отклонениях от положения равновесия на одинаковый угол.
29Шарик подвешен на длинной нити. В первом опыте его поднимают по вертикали до точки подвеса и отпускают. Во втором опыте его отклоняют на малый угол и снова отпускают. Каждый раз фиксируют время возврата шарика в положение равновесия. Определить отношение θ времени возврата шарика в положение равновесия в первом опыте к аналогичному времени во втором опыте.
30Медный шарик (ρ1 = 8900 кг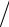 м3 ), подвешенный к пружине, совершает малые вертикальные колебания. Рядом колеблется на точно такой же пружине алюминиевый шарик (ρ2 = 2700 кг
м3 ), подвешенный к пружине, совершает малые вертикальные колебания. Рядом колеблется на точно такой же пружине алюминиевый шарик (ρ2 = 2700 кг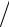 м3 ) такого же радиуса. Найти отношение μ периода колебаний медного шарика к аналогичной величине алюминиевого шарика.
м3 ) такого же радиуса. Найти отношение μ периода колебаний медного шарика к аналогичной величине алюминиевого шарика.
31Математический маятник на поверхности Земли колеблется с периодом
|
T0 |
= 2 c . На |
какое время |
T |
изменится период колебаний такого |
|
|
маятника при подъеме на высоту |
H = 320 км над поверхностью Земли. |
||||
|
Радиус Земли принять равным R = 6400 км. |
|
||||
32 |
В |
некоторый |
момент времени |
две частицы находятся на расстоянии |
||
|
L |
= 10 км друг от друга и движутся навстречу друг другу со скоростями |
||||
|
υ1 |
= 0,4c и |
υ2 = 0,6c ( c −скорость света). Через какое время |
T |
||
|
частицы столкнутся? |
|
|
|
||
33 |
Звездный корабль путешествовал |
по собственным часам T0 = 10 лет, |
||||
|
двигаясь со скоростью υ = 0,8c ( c −скорость света). На какое время |
T |
||||
земляне будут старше космонавтов, когда корабль вернется на Землю?
34C какой скоростью υ должен лететь космический корабль от Земли до
некоторой звезды, чтобы собственное время полета космонавтов было в n = 2 раза больше времени, необходимого свету для преодоления того же
пути?
35Свет до некоторой звезды идет Tc = 4 года. Чему равно собственное
время t0 , необходимое для полета космонавтам до этой звезды, если космический корабль будет двигаться со скоростью υ = 0,9c ( c −скорость
|
света)? |
|
|
|
|
|
|
|
|
|
36 |
Поперечная |
волна распространяется |
вдоль |
упруго |
шнура |
со |
скоростью |
|||
|
υ = 10 м/c . Амплитуда |
колебаний |
точек шнура |
A = 20 cм, |
а период |
|||||
|
колебаний T = 1 c . |
Определить смещение точки |
s1, расположенной на |
|||||||
|
расстоянии |
x1 = 10 м |
от источника колебаний |
в момент |
времени |
|||||
|
t1 = 3 c . |
|
|
|
|
|
|
|
|
|
37 |
Поперечная |
волна распространяется |
вдоль |
упруго |
шнура |
со |
скоростью |
|||
|
υ = 10 м/c . Амплитуда |
колебаний |
точек шнура |
A = 20 cм, |
а период |
|||||
|
колебаний |
T = 1 c . |
Определить |
скорость |
& |
= ds1 dt |
точки s1, |
|||
|
s1 |
|||||||||
|
|
|
|
- 66 - |
|
|
|
|
|
|

|
расположенной |
на расстоянии |
x1 = 2,5 м от источника |
колебаний в |
||||||||
|
момент времени t1 = 3 c . |
|
|
|
|
|
|
|
|
|
||
38 |
Поперечная |
волна распространяется |
вдоль упруго |
шнура со |
скоростью |
|||||||
|
υ = 10 м/c . Амплитуда колебаний |
точек шнура A = |
20 cм, |
а период |
||||||||
|
колебаний |
T = |
|
|
|
&& |
2 |
s1 dt |
2 |
точки s1, |
||
|
|
|
|
|
|
|||||||
|
1 c . Определить ускорение s1 = d |
|
|
|||||||||
|
расположенной на расстоянии x1 = 5 м от источника колебаний в момент |
|||||||||||
|
времени t1 = 3 c . |
|
|
|
|
|
|
|
A = 1 мм |
|||
39 |
Звуковые колебания с частотой ν = 450 Гц и амплитудой |
|||||||||||
|
распространяются в упругой среде. Длина волны составляет |
λ = 80 cм. |
||||||||||
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
Определить максимальную скорость smax частиц среды. |
|
|
|
|
|||||||
40 |
Плоская синусоидальная волна распространяется вдоль прямой, |
|||||||||||
|
совпадающей с |
положительным |
направлением оси |
OX со |
скоростью |
|||||||
|
υ = 10 м/c и амплитудой |
A = 20 cм. Две точки А и В, находящиеся на |
||||||||||
|
расстоянии |
x1 = 7 м и x2 = 10 м от источника колебаний, |
колеблются с |
|||||||||
|
разностью фаз |
ϕ = 0,6π рад. Написать уравнение |
s = s(t, x) |
такой |
||||||||
|
волны. Среда, в которой распространяется волна, не поглощает энергию. |
|||||||||||
41 |
Плоская синусоидальная волна распространяется вдоль прямой, |
|||||||||||
|
совпадающей с |
положительным |
направлением оси |
OX со |
скоростью |
|||||||
|
υ = 10 м/c и амплитудой |
A = 20 cм. Две точки А и В, находящиеся на |
||||||||||
|
расстоянии |
x1 = 7 м и x2 = 10 м от источника колебаний, |
колеблются с |
|||||||||
|
разностью фаз |
ϕ = 0,6π рад. Определить смещение |
s2 второй точки в |
|||||||||
|
момент времени |
t2 = 5 c. |
Среда, в которой распространяется волна, не |
|||||||||
|
поглощает энергию. |
|
|
|
|
|
|
|
|
|
||
42 |
Плоская синусоидальная волна распространяется вдоль прямой, |
|||||||||||
|
совпадающей с |
положительным |
направлением оси |
OX со |
скоростью |
|||||||
|
υ = 10 м/c и амплитудой |
A = 20 cм. Две точки А и В, находящиеся на |
||||||||||
|
расстоянии |
x1 = 7 м и x2 = 10 м от источника колебаний, |
колеблются с |
|||||||||
|
разностью фаз |
ϕ = 0,6π рад. Определить смещение |
s1 первой точки в |
|||||||||
|
момент времени |
t1 = 3 c . |
Среда, в которой распространяется волна, не |
|||||||||
|
поглощает энергию. |
|
|
|
|
|
|
|
|
|
||
43 |
Плоская синусоидальная волна распространяется вдоль прямой, |
|||||||||||
|
совпадающей с положительным направлением оси OX в не поглощающей |
|||||||||||
|
энергию среде. Две точки А и В, |
находящиеся на расстоянии x1 = 7 м и |
||||||||||
|
x2 = 10 м |
от |
источника |
колебаний, колеблются |
|
с |
разностью |
фаз |
||||
|
ϕ12 = 0,6π рад. Третья точка D, находящаяся правее токи B на оси |
|||||||||||
|
OX, имеет с точкой B разность фаз |
ϕ23 = 2,3π рад. Найти разность |
||||||||||
|
фаз ϕ13 , с которой колеблются точки А и D. |
|
|
|
|
|
|
|||||
44Через какое время T после выстрела артиллерист услышит звук разрыва снаряда, если снаряд вылетел из ствола орудия со скоростью
-67 -
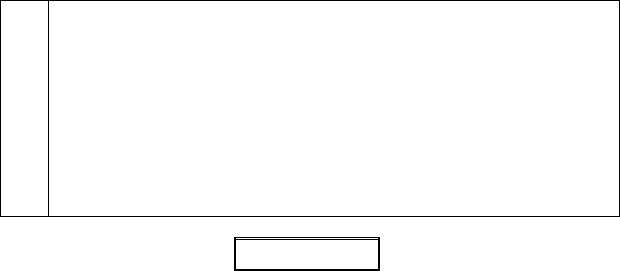
υ0 = 600 м/c |
под углом α = 45o |
к горизонту. |
Скорость звука равна |
υ = 340 м/c . |
|
|
|
45 Шарик подвешен на нити длиной L = 2 м. В первом опыте его поднимают |
|||
по вертикали |
до точки подвеса и |
отпускают с |
начальной скоростью |
υ0 = 1 м/c . Во втором опыте его отклоняют на малый угол и снова
отпускают. Каждый раз фиксируют время возврата шарика в положение равновесия. Определить отношение θ времени возврата шарика в положение равновесия в первом опыте к аналогичному времени во втором опыте.
***** §10 *****
- 68 -
§11. «Усеченные» решения задач и ответы |
|
||||
|
|
Задача1 |
|
|
|
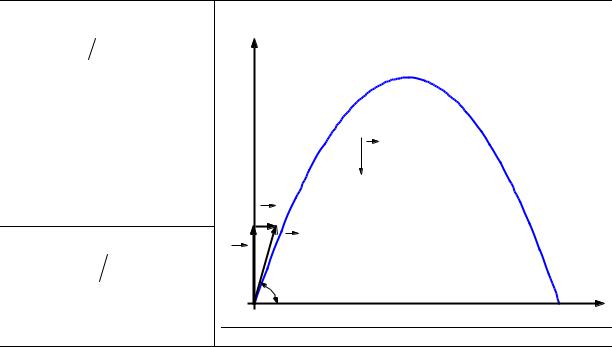
Из вращающегося вокруг вертикальной оси жесткого шланга бьет струя воды, |
|||||
вылетающая со скоростью υ0 =10 м/с под углом α = 30° |
к горизонту. Чему |
||||
равна площадь круга |
S , |
затапливаемая водой. Сопротивление воздуха |
|||
уменьшает на η = 25% дальность полета струи по горизонтали. |
|
||||
1*. Дано: |
|
|
Решение. |
|
|
υ0 = 10м с, |
|
Y |
Движение материальной точки, брошенной |
||
|
|
2*. |
под углом к горизонту |
|
|
α = 30°, |
|
|
|
|
|
|
|
.g |
|
|
|
η = 25%. |
|
|
|
|
|
|
|
|
|
|
|
|
|
v0x |
|
|
|
S – ? |
|
v0 |
|
|
|
g = 9,81 м с2 |
|
v 0y |
|
L.B |
|
|
O.α |
|
X |
||
|
|
|
|||
4*. Составим полную систему уравнений для нахождения |
|||||
искомой величины S : |
|
|
|
|
|
|
|
0 =υ0yTB |
|
|
|
2 |
, |
|
(1) |
− gTB |
|||||
|
|
|
2 |
|
|||
|
(2) |
υ0y =υ0 sinα, |
|
|
|||
|
|
L =υ0 xTB , |
|
|
|||
|
(3) |
|
|
||||
|
|
υ0 x =υ0 cosα, |
|
|
|||
|
(4) |
|
|
||||
|
(5) |
S = πR2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
η |
|
|
|
|
(6) |
R = L 1 − |
|
|
|
. |
|
|
100 |
|
|
||||
|
|
|
|
|
|
||
Система шести уравнений (1) – (6) замкнута, так как |
|||||||
содержит шесть неизвестных величин: υ0y , υ0x , TB , L, R, S . |
|||||||
9*. Ответ: |
S ≈1,4 102м = 140 м . |
|
|||||
***************
- 69 -
|
Задача2 |
|
|
||
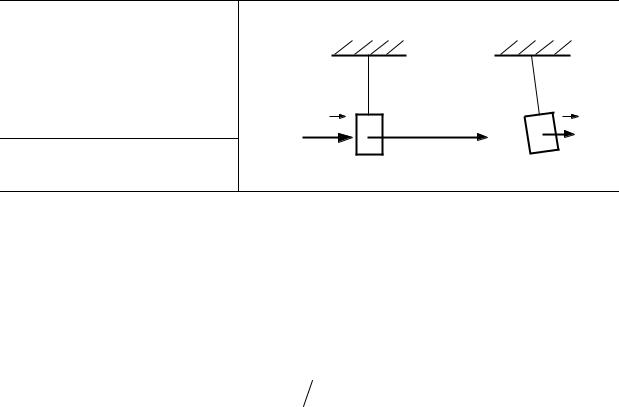
В мешке с песком массой M = 3 кг, висящем на подвесе, застревает летевшая |
|||||
горизонтально со скоростью υ = |
700 м/с пуля массой m = 20 г. Найти долю |
||||
энергии η , перешедшую в немеханические формы, от энергии, которой обладала |
|||||
пуля до удара. |
|
|
|
|
|
1*. Дано: |
2*. |
|
Решение. |
|
|
M = 3 кг, |
|
|
|
||
m = 20 г= 2 10−2 кг, |
|
|
|
. u |
|
υ = 700 м/с. |
.m |
v |
.O M |
||
η – ? |
|||||
|
|
|
X |
||
4*. Составим полную систему уравнений для нахождения |
|||||
искомой величины η : |
|
|
|
|
|
|
mυ |
2 |
(m + M )u |
2 |
E , |
|||
(1) |
= |
+ |
||||||
|
2 |
|
|
|
2 |
|
|
|
|
mυ = (m + M )u, |
|
|
|||||
(2) |
|
|
||||||
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
||
η = |
|
|
2 |
. |
|
|
||
(3) |
|
mυ |
|
|
||||
|
|
|
|
2 |
|
|
|
|
Система трех уравнений (1) – (3) замкнута, так как содержит три неизвестные величины: u, E, η .
9*. Ответ: η ≈ 9,9 10−1 (не зависит от υ ).
***************
Задача3
Определить молярную массу М смеси кислорода (масса и молярная масса соответственно равны m1 = 2,5 г и M1 = 32 г/моль) и азота
(масса и молярная масса - m2 = 7,5 г и M2 = 28 г/моль ).
1*. Дано: |
Решение. |
||
m = 2,5 |
г=2,5 10−3 кг, |
2*. -------- |
|
1 |
г/моль=3,2 10−2 кг/моль, |
|
|
M1 = 32 |
4*. Составим полную |
||
m2 = 7,5 г=7,5 10−3 кг, |
систему |
уравнений для |
|
M2 = 28г/моль=2,8 10−2 кг/моль. |
нахождения |
искомой |
|
|
|
величины М: |
|
|
|
|
|
- 70 -
