Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Коломенский институт филиал МГМУ

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Задачник по физике

.pdf

Скачиваний:

Добавлен:

17.03.2016

Размер:

2.49 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 1819 / 2219 20 21 22 > Следующая >>>

1*. Дано:					Решение.
i = 6,				2*.--------
i = 6,				4*. Составим полную
p = 202 кПа = 2,02 105 Па ,				4*. Составим полную
t = 27oC ,			систему		уравнений		для
t = 27oC ,			нахождения			искомой
V = 10 л = 10−2м3 .			нахождения			искомой
V = 10 л = 10−2м3 .					′	:
			величины CV			:

′	(моль К).
CV –? R = 8,31 Дж	(моль К).
	(1)		Cp′ = CV ν,
			CV = iR 2,
	(2)		CV = iR 2,
			pV =νRT ,
	(3)		pV =νRT ,
			T = t + 273,15 .
	(4)		T = t + 273,15 .
Система четырех уравнений				(1) –	(4) замкнута,		так как
содержит четыре неизвестные величины:					′
содержит четыре неизвестные величины:					CV , CV ,ν , T .
9*. Ответ:	′	1 Дж			Дж
9*. Ответ:	CV ≈ 2,0	10		К = 20 К .

***************

Задача127

Два математических маятника колеблются с одинаковой угловой амплитудой, но первый маятник имеет в q = 2 раза большую длину. Определить отношение θ

полной энергии первого маятника к полной энергии второго маятника в сходственных точках колебательного процесса, то есть при отклонениях от положения равновесия на одинаковый угол.

1*. Дано:				Решение.
q = 2 .	2*.	точка
	2*.	подвеса
			.

		ось качания	C
	перпендикулярна
		чертежу
		ϕ0
θ – ?		ϕ0
θ – ?
			1
				L

H.1 .

ϕ0

L 2

H.2 .

- 181 -

4*. Составим полную систему уравнений для нахождения

искомой величины θ :

W1 = mgH1 = mgL1

(1 − cosϕ0 ),

(1)

(2)

= mgH

= mgL

(1 − cosϕ

= q,

(3)

W1 =θ.

(4)

Система четырех уравнений (1) – (4) замкнута, так как

содержит

четыре

неизвестные

величины:

(W1 W2 ),(m(1 − cosϕ0 )), (L1

L2 ),θ .

9*. Ответ:

θ = 2,0 .

***************

Задача128

Шарик подвешен на длинной нити. В первом опыте его поднимают по вертикали

до точки подвеса и отпускают. Во втором опыте его отклоняют на малый угол и

снова отпускают. Каждый раз фиксируют время возврата шарика в положение

равновесия.

Определить отношение θ времени возврата шарика в положение

равновесия в первом опыте к аналогичному времени во втором опыте

1*. Дано:

2*.

Решение.

точка

подвеса

ось качания .C

перпендикулярна

чертежу

ϕ0

№1

θ −?

опыт

H.1

опыт №2

4*.

Составим полную систему уравнений для нахождения

искомой величины θ :

- 182 -

	L =	2	,
(1)	L =	gt1	,
		2
	t2 =	T ,
(2)	t2 =	T ,
		4
	T =	2π	,
(3)	T =	ω	,
		ω
	ω =	g
(4)	ω =	g
		L
	θ =	t
(5)	θ =	1 .
		t2

Система пяти уравнений (1) – (5) замкнута, так как

содержит пять неизвестных величин: T , L, ω, θ, t1 . t2

9*. Ответ: θ = 2π2 ≈ 9,0 10−1 = 0,9.

***************

Задача129

Медный шарик (ρ1 = 8900 кгм3 ), подвешенный к пружине, совершает малые вертикальные колебания. Рядом колеблется на точно такой же пружине алюминиевый шарик (ρ2 = 2700 кгм3 )такого же радиуса. Найти отношение μ периода колебаний медного шарика к аналогичной величине алюминиевого шарика.

1*. Дано:			Решение.	.
ρ1 = 8900 кг м3 ,	2	*.		.
ρ2 = 2700 кг м3 .	2	*.	k	k
			k	k
			.m1
				m2
μ– ?				m2

4*. Составим полную систему уравнений для нахождения искомой величины μ:

- 183 -

(1)	ω	=		k ,
	1		m1
			m1
	m1 =		4	πR3ρ1,
(2)	m1 =		4	πR3ρ1,
			3
(3)	T1 = 2π ω1 ,
				k
	ω2	=		k	,
(4)	ω2	=	m2		,
			m2
	m2 =		4	πR3ρ2,
(5)	m2 =		4	πR3ρ2,
			3
(6)	T2 = 2π ω2 ,
(7)	μ	= T		T .
			1	2

		Система семи уравнений (1) – (7) замкнута, так как
содержит			семь	неизвестных			величин:
(ω1		k ), (ω2	k ), (m1 R),	(m2 R), T1, T2 , μ.
9*. Ответ:				μ ≈ 1,8 .
			***************
				Задача130
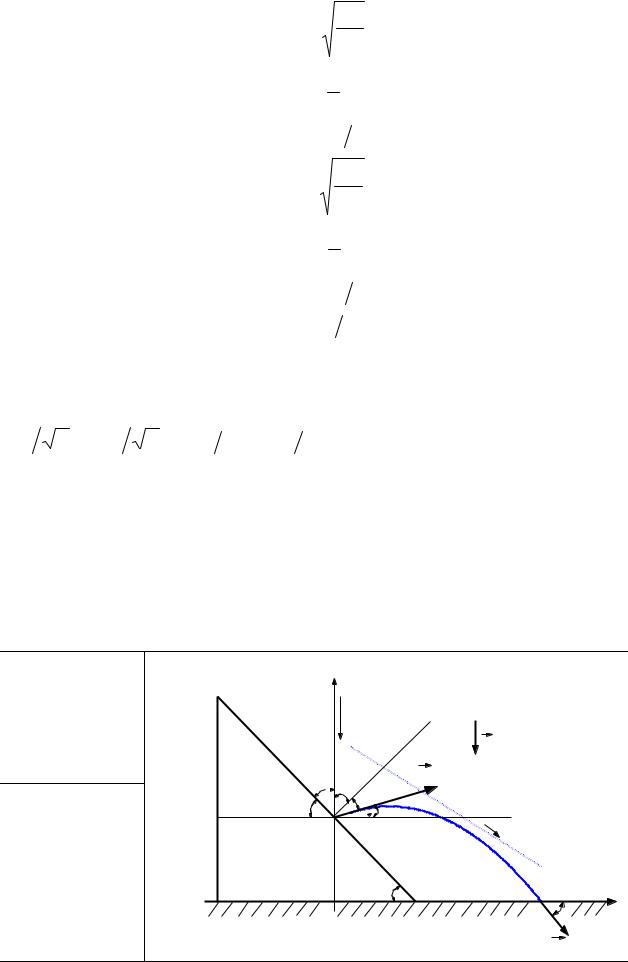
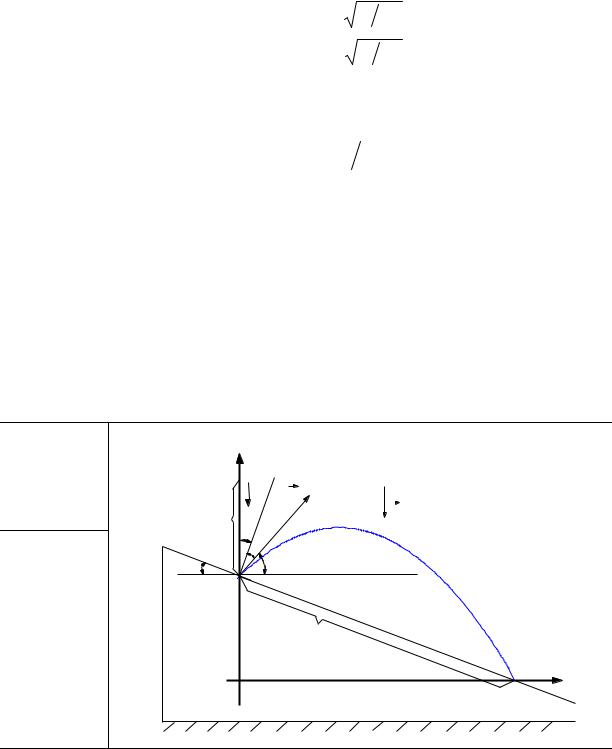
Мяч падает с высоты H =10 м. На высоте h = 2 м от поверхности земли он
абсолютно упруго ударяется о наклонную плоскость, расположенную под углом
α = 30° к горизонту. Найти время T2 движения мяча после удара о наклонную
плоскость.
1*. Дано:					Решение.
H	=	10 м,		HY.A
H		10 м,		.				2*.
h = 2 м,								2*.
h = 2 м,							g
α = 30°.							g
α = 30°.						vB
T	– ?			(π−α)		vB
T	– ?			α		β=α
2				α h.
				α h.		γ=π\|2−2α
				B
				0.		α	.Dϕ	X
				0.			S
							vD
				- 184 -

4*. Составим полную систему уравнений для нахождения искомой величины T2 :

(1)			h = H − gT				2	2,
						B
			−υB = −gTB ,
(2)			−υB = −gTB ,
			0 = h +υByTD − gTD2							2,
(3)			0 = h +υByTD − gTD2							2,
			υBy =υB cos2α,
(4)			υBy =υB cos2α,
(5)			T		= T .
			2			D
Система пяти уравнений (1) – (5) является замкнутой, так
как содержит пять неизвестных величин: TB ,υB ,υBy , TD, T2 .
9*. Ответ:					T2 ≈1,5 c .
		***************
					Задача131
Зависимость пройденного	телом				пути от		времени			задается уравнением
s = (A + Bt + Ct 2 + Dt3 )м,			где A = 6 м,					B = −3 м/ с,			C = 2 м/ с2 ,
D = 1 м/ с3 . Определить среднее ускорение							a за промежуток времени от
T1 =1c до T2 = 4 c.
1*. Дано:								Решение.
s = (A + Bt + Ct 2 + Dt3 )м,						2*.--------
s = (A + Bt + Ct 2 + Dt3 )м,						4*. Составим полную систему
A = 6 м,						4*. Составим полную систему
B = −3 м/ с,					уравнений			для			нахождения
C = 2 м/ с2 ,					искомой величины a :
C = 2 м/ с2 ,
T1 =1c,
T2 = 4 c.
a – ?

				s T		− s T
(1)	a		&			&	,
(1)	a		=		2	1	,
					T2 −T1
	&		=		B + 2CT		+	3DT	2	,
(2)	s	T1	=		B + 2CT		+	3DT		,
		T1				1		1
									2
	&		=						2
(3)	s T2		=		B + 2CT2 + 3DT2 .

- 185 -

Система трех

уравнений

(1)

–

(3)

замкнута,

так

как

содержит три неизвестные величины:

a , s T

, s T .

9*. Ответ:

= 1,9 101 м с2 = 19 м с2 .

***************

Задача132

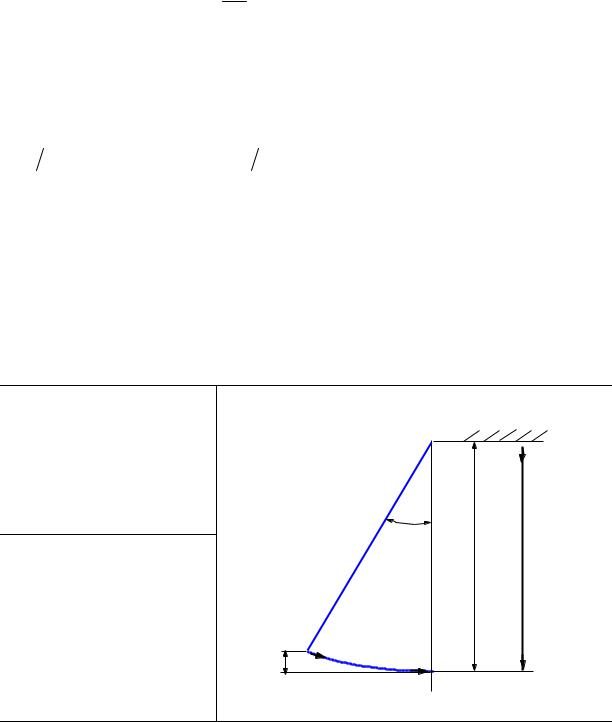
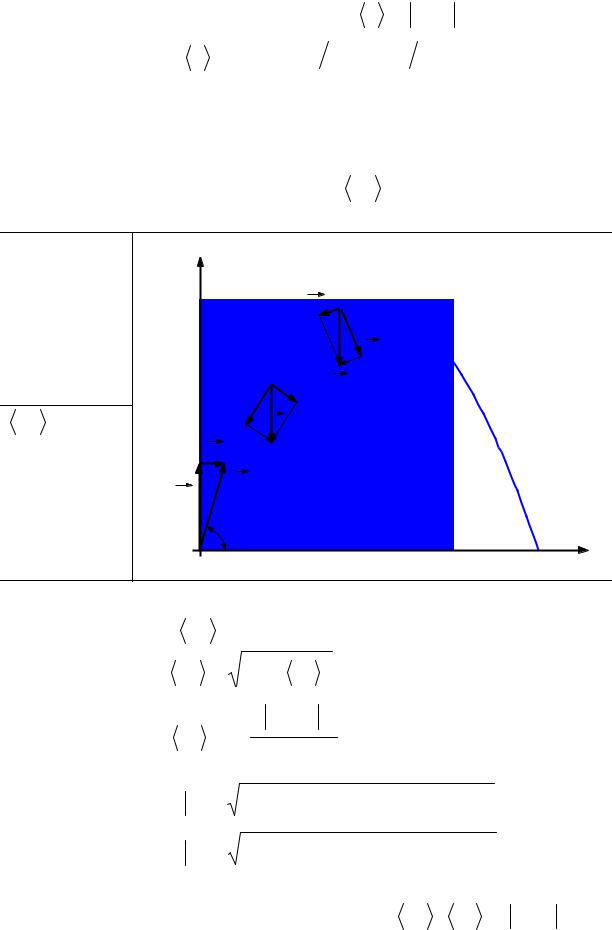
Тело брошено под углом ϕ = 30° к горизонту со скоростью υ0 = 10 м/с. Найти

среднее центростремительное ускорение

аn

за

промежуток

времени от

T1 =1c до T2 = 5 c после броска. Сопротивлением воздуха пренебречь.

1*. Дано:

Решение.

2*.

ϕ = 30°,

a τ

υ0 = 10 м/с,

T1 =1c,

an(T2)

T2 = 5 c.

(T )

aτ

аn – ?

v0x

v0y

O.α

L.B

4*. Составим полную систему уравнений для нахождения

искомой величины

аn

(1)

g2 −

υ T

−υ T

(2)

−T

(υ

cosϕ)2

(υ

sinϕ

− gT )2 ,

(3)

(υ

cosϕ)2

(υ

− gT )2 .

(4)

sinϕ

Система четырех уравнений (1) – (4) замкнута, так как

содержит четыре неизвестные величины: an , aτ , υ T1

, υ T2 .

- 186 -

9*. Ответ:	аn ≈ 9,7м с2 .
	***************
	Задача133	ν = 50 c−1,
Якорь электродвигателя, имеющий частоту вращения		ν = 50 c−1,	после
выключения сделал	N = 238 оборотов и остановился.	Определите	угловое

ускорение ε якоря в предположение, что его движение было равнозамедленным.

1*. Дано:				Решение.
ν = 50 c−1,	2*.--------
ν = 50 c−1,	4*.		Составим				полную	систему
N = 238.	4*.		Составим				полную	систему
	уравнений			для нахождения				искомых
ε – ?	уравнений			для нахождения				искомых
g = 9,81 м с2 .	величин ε :
	(1)	ϕ = 2πN ,
					εT		2
		ϕ	= ω0T −		εT		2
	(2)	ϕ	= ω0T −			2	,
						2
	(3)	ω	0	= 2πν ,
			0
		0 = ω0 − εT .
	(4)	0 = ω0 − εT .

Система четырех уравнений (1) – (4) замкнута, так как содержит четыре неизвестные величины: ϕ, ω0 , T , ε .

9*. Ответ: ε ≈ 3,3 101 рад c2 = 33 рад c2 .

***************

Задача134

Математический маятник на поверхности Земли колеблется с периодом T0 = 2 c .

На какое время	T изменится период колебаний такого маятника при подъеме
на высоту H = 320 км над поверхностью Земли. Радиус Земли и масса равны
R = 6400км и M = 6 1024кг.			Решение.
1*. Дано:
T0 = 2 c ,		2*.--------
		4*.	Составим	полную
H = 320 км = 3,2 105 м,
R = 6400 км = 6,4 106 м,		систему	уравнений для
		нахождения		искомой
M = 6 1024кг, g = 9,81 м с2 .
		величины	T :
T – ?γ = 6,67 10−11Н м2/кг2 .

- 187 -

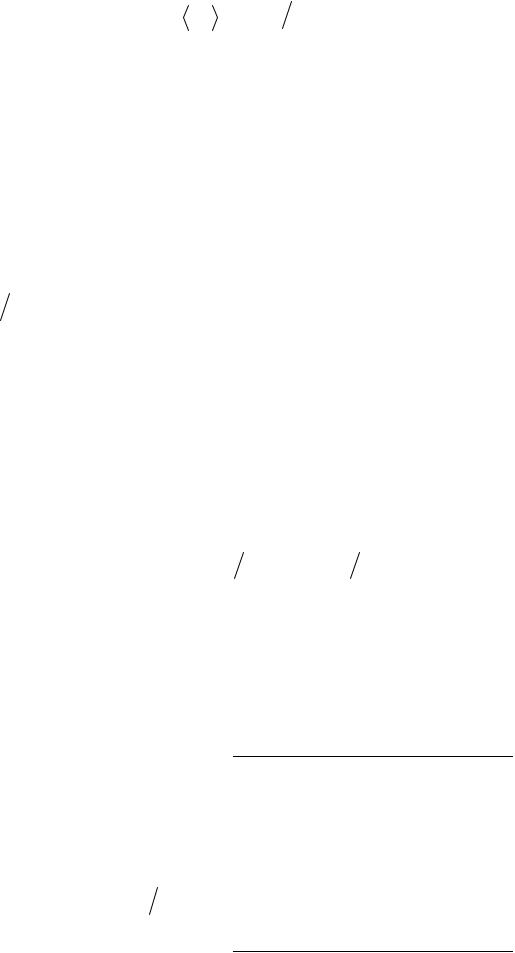
	(1)	T0 = 2π		L g0 ,
		T1 = 2π		L g1 ,
	(2)	T1 = 2π		L g1 ,
		T = T1 −T0 ,
	(3)	T = T1 −T0 ,
		g0 = g,
	(4)	g0 = g,
	(5)	g	= γM (R + H )2 .
		1
Система пяти уравнений (1) – (5) замкнута, так как содержит
пять неизвестных величин:		L, g0 , T1, g1, T .
9*. Ответ:	T ≈ 1,0 10−1c = 0,1 c .
	***************
	Задача135
Шарик свободно падает с высоты			H = 1 м		на наклонную	плоскость,
составляющую с горизонтом угол α = 30°. Упруго отразившись от наклонной
плоскости, он второй раз падает на ту же плоскость. Найти расстояние						S между
точками соприкосновения шарика и плоскости.
1*.	Y		Решение.		2*.
	Y
Дано:	.A
Дано:	.A
H = 1 м,		vB		g
H = 1 м,
α = 30°.	H
α = 30°.	H
S – ?	β=α
S – ?	α
α	B.	γ=π/2−2α
			S
	0.				.D	X
					L
4*. Составим полную систему уравнений для нахождения
искомой величины S :
		- 188 -

	(1)	S sinα = H + S sinα − gT 2 2,
							B
		−υB = −gTB ,
	(2)	−υB = −gTB ,
	(3)	0 = S sinα +υ			By	T	− gT 2 2,
					By	D	D
		υBy =υB cos2α =υB (2cos2 α −1),
	(4)	υBy =υB cos2α =υB (2cos2 α −1),
		L = S cosα ,
	(5)	L = S cosα ,
	(6)	L =υ		T ,
				Bx D
		υBx =υB sin 2α = 2υB sinα cosα.
	(7)	υBx =υB sin 2α = 2υB sinα cosα.

Система семи уравнений (1) – (7) замкнута, так как
содержит семь неизвестных величин:							S,TB ,υB ,TD ,υBy , L,υBx .
9*. Ответ:				S = 4,0 м.
			***************
				Задача136
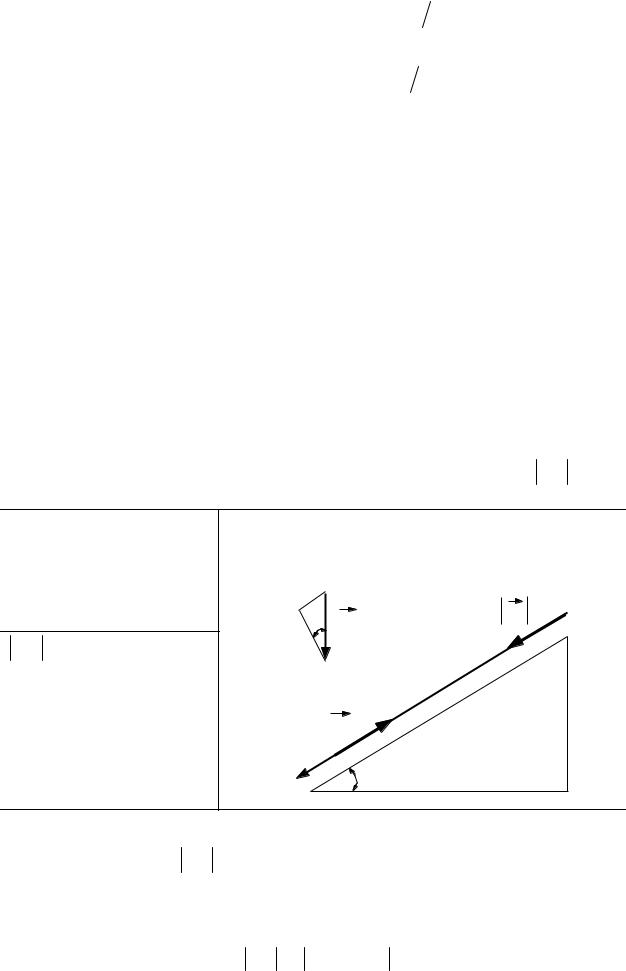
По наклонной плоскости, длина которой						L = 2,5 м одновременно начали
двигаться два тела: P1		– вверх с начальной скоростью υ1 = 50 см/с,						P2 –
вниз без начальной скорости (υ2 = 0). Какова относительная скорость υ12								тел в
месте встречи в системе отсчета, связанной с плоскостью?
1*. Дано:				2*.			Решение.
L = 2,5 м,				2*.
L = 2,5 м,
υ1 = 50 см/с = 0,5 м/с,				g *sinα			0
υ2 = 0 м/с.						g	0
υ2 = 0 м/с.						g	v2 =0 .
υ12 – ?					α		P2
υ12 – ?							.S
					Lv1		.S
					Lv1		P
				X .			1
						α
4*.	Составим полную систему уравнений для нахождения
искомой величины υ12 :
		(1)	υ1S = −υ1 + gsinαT ,
			υ2S =υ2 + gsinαT ,
		(2)	υ2S =υ2 + gsinαT ,
				υ12 = υ1S −			υ2S .
		(3)		υ12 = υ1S −			υ2S .
				- 189 -

Система трех уравнений (1) – (3) не замкнута, так как содержит четыре неизвестные величины: υ1S , υ2S , υ12 , (sinαT ).

Однако уравнения (1) – (3) линейно зависимы относительно
величин υ1S , υ2S ,	(sinαT ).
9*. Ответ:		υ12	=	υ1 +υ2	= 5,0 10−1 м/с = 50 см/с.

	***************
			Задача137
Звездный корабль путешествовал по собственным часам T0 = 10 лет, двигаясь
со скоростью υ = 0,8c ( c −скорость света). На какое время T земляне будут

старше космонавтов, когда корабль вернется на Землю?

1*. Дано:		Решение.
T = 10 лет=3,6 103	24 365 10 с,	2*.--------
0		4*.	Составим
υ = 0,8c .		4*.	Составим
υ = 0,8c .		полную	систему
		полную	систему
		уравнений	для
T – ?		уравнений	для
T – ?		нахождения	искомой
		нахождения	искомой
		величины	T :

	T =	T0		,
(1)	T =		υ2	,
		1 −	υ2
		1 −	c2
			c2
(2)	T	= T −T .
			0

Система двух уравнений (1) – (2) замкнута, так как содержит две неизвестные величины: T, T .

9*. Ответ:	T ≈ 2,1 108c = 6,7 лет.
	***************
	Задача138

Свет до некоторой звезды идет Tc = 4 года. Чему равно собственное время t0 ,

необходимое для полета космонавтам до этой звезды, если космический корабль будет двигаться со скоростью υ = 0,9c ( c −скорость света)?

1*. Дано:			Решение.
T = 4 года=3,6 103	24 365* 4 с,	2*.--------
c		4*.	Составим полную
υ = 0,9c .		4*.	Составим полную
υ = 0,9c .		систему	уравнений для
		систему	уравнений для

- 190 -

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 1819 / 2219 20 21 22 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.05.2025128.06 Кб0Ж.-Б. Мольер Мизантроп.docx
#
06.11.201859.39 Кб1жаргон.doc
#
19.09.20193.05 Mб4Задание 1 часть_В1-В34.docx
#
17.03.201650.22 Кб16Задание1.docx
#
17.03.2016172.54 Кб39Задачи_БФО.doc
#
17.03.20162.49 Mб93Задачник по физике.pdf
#
27.11.201983.37 Кб10Западноевропейское общество и государство X-XI...docx
#
01.04.202516.19 Mб1записка САПР.doc
#
01.03.202571.53 Кб0зачет страхование.docx
#
01.05.202563.97 Кб0Зачет ЭЛЕКТРОДИНАМИКА карусель.docx
#
12.11.2019149.5 Кб6Зачетное задание по НИРс2.doc