22.2. Представления автомата

Конечный автомат удобно представлять таблицей переходов и таблицей выходов. Строкам этих таблиц соответствуют состояния автомата, столбцам – входные символы. На пересечении строки, соответствующей состоянию q, и столбца, соответствующего входному символу а, в таблице переходов

записывается значение Ψ(a, q), а в таблице выходов – значение Φ(a, q). Другими словами, в первом случае в клетке таблицы указывается состояние, в которое автомат переходит из состояния q при поступлении на его вход символа а, а во втором случае – выходной символ, который при этом выдает автомат. Табл. 22.2 и табл. 22.3 представляют собой пример описанного представления автомата Мили, у которого А = {a1, a2, a3, a4}, В = {b1, b2} и

Q = {q1, q2, q3}.

Зная начальное состояние автомата и входную последовательность, нетрудно получить по этим таблицам соответствующую последовательность выходных символов. Приведем пример такого соответствия для автомата, заданного табл. 22.2 и 22.3, на вход которого поступила последовательность символов а1, а2, а2, а1, а3, а4, а1, а4 при начальном состоянии q1. Покажем также состояния, которые проходит автомат:

Автомат Мура представляется одной таблицей переходов, к которой добавлен один столбец со значениями функции выходов (табл. 22.4).

Можно свести таблицу переходов и таблицу выходов автомата Мили в одну таблицу, которую называют таблицей переходов и выходов. Такая таблица для автомата, заданного в виде табл. 22.2 и табл. 22.3, имеет вид табл. 22.5.

Более наглядным при небольшом числе состояний является представление автомата в виде графа поведения автомата, который представляет собой ориентированный граф. Его вершины соответствуют состояниям автомата, а дуги – переходам между состояниями. При этом дуга помечается всеми входными символами, которые вызывают соответствующий переход, и выходными символами, сопровождающими данный переход (в случае автомата

147

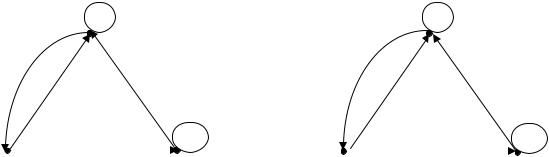
Мили). В случае автомата Мура выходными символами помечаются вершины, соответствующие состояниям, в которых находится автомат при выдаче данных символов. На рис. 22.1 изображены графы переходов автоматов, заданных табл. 22.4 и 22.5.

Рис. 22.1. Примеры графов поведения: а) автомата Мура; б) автомата Мили

Еще одним способом представления автомата является матрица поведения, представляющая собой квадратную матрицу, строки и столбцы которой помечаются состояниями автомата. В случае автомата Мура на пересечении строки qi и столбца qj матрицы поведения записываются входные символы, переводящие автомат из состояния qi в состояние qj, а строки помечаются также и выходными символами. В случае автомата Мили элементы матрицы поведения, кроме входных символов, вызывающих соответствующие переходы, содержат выходные символы, которые сопровождают эти переходы. Если из состояния qi нет перехода в состояние qj, то на пересечении строки qi и столбца qj ставится прочерк. Для рассмотренных автоматов ниже представлены матрицы поведения, причем первая из них – матрица поведения автомата Мура, вторая – матрица поведения автомата Мили.

148

22.3. Связь между моделями Мили и Мура

Всякое отображение входных последовательностей в выходные может быть реализовано как с помощью модели Мили, так и с помощью модели Мура. Определим преобразование, переводящее любой автомат Мили в эквивалентный ему автомат Мура, а также преобразование, переводящее любой автомат Мура в эквивалентный ему автомат Мили.

Пусть задан автомат Мура М = (A, B, Q, Ψ, Φ) и требуется получить

эквивалентный ему автомат Мили М = (A , B , Q , Ψ , Φ ).

Очевидно, А = А и В = В. Положим Q = Q и Ψ = Ψ, а Φ определим следующим образом. Пусть Ψ(a, q) = q′ и Φ(q′) = b, где q, q′ Q, a А и b В. Это означает, что автомат, будучи в состоянии q, отвечает на входной символ а выходным символом b, который выдается в следующий момент времени, когда автомат окажется в состоянии q′. Следовательно, можно считать, что

Φ (а, q) = b. Автомат Мура и эквивалентный ему автомат Мили представлены в табл. 22.6 и 22.7 соответственно.

Пусть теперь задан автомат Мили М = (A, B, Q, Ψ, Φ) и требуется получить эквивалентный ему автомат Мура М = (A , B , Q , Ψ , Φ ). Как и в предыдущем случае, имеем А = А и В = В. Определим Q следующим образом. Рассмотрим все такие пары вида (q, b), где q Q, b B, что для каждой (q, b) имеется такая пара (a, q′), что Ψ(a, q′) = q и Φ(a, q′) = b (a A, q′ Q). Каждой паре (q, b) поставим в соответствие состояние q Q и определим функции Ψ и Φ следующим образом:

Если автомат имеет состояние, в которое он никогда не переходит (это может быть начальное состояние), то всякому такому состоянию ставится в

149

соответствие состояние автомата Мура, переходы из него определяются аналогично, а выходной символ при нем не определен.

Если автомат является частичным, то достаточно ввести новое состояние, соответствующее неопределенному состоянию, и новый выходной символ, соответствующий неопределенному выходному символу, и после описанных преобразований вернуться к неопределенному состоянию и неопределенному выходному символу. Переходы из такого состояния не определены. Автомат Мили и эквивалентный ему автомат Мура представлены в табл. 22.8 и 22.9 соответственно.

22.4. Автомат с абстрактным состоянием. Булев автомат

Широко распространенным типом автомата является модель, описываемая одной многозначной внутренней переменной q и многими входными и выходными булевыми переменными х1, х2, … , хп и у1, у2, … , ут. Поведение такого автомата задается системой уравнений

q+ = ψ(х1, х2, … , хп; q); y1 = ϕ1(х1, х2, … , хп; q);

y2 = ϕ2(х1, х2, … , хп; q);

…

ym = ϕm(х1, х2, … , хп; q),

более компактно представляемой в векторной форме

q+ = ψ(х, q); y = ϕ(х, q).

Функции ψ и ϕ отличаются от введенных ранее Ψ и Φ только тем, что многозначные входная и выходная переменные оказались замененными на соответствующие булевы векторы, но внутренняя переменная осталась многозначной.

150

Описанная модель называется автоматом с абстрактным состоянием.

Ею удобно пользоваться на начальных этапах логического проектирования дискретных устройств, когда вход и выход устройства описываются как некоторые множества булевых переменных, имеющих конкретную техническую интерпретацию, в то время как множество внутренних переменных представляется пока в простейшей форме, в виде одной многозначной переменной q. Число значений переменной q полагается равным числу различных состояний автомата, при котором он может реализовать заданное функциональное отношение между входом и выходом.

Если заменить внутреннюю переменную q на соответствующий булев вектор z = (z1, z2, … , zk), то получится система уравнений, в которой все переменные и все функции оказываются булевыми:

z1+ = ψ1(х1, х2, … , хп; z1, z2, … , zk); z2+ = ψ2(х1, х2, … , хп; z1, z2, … , zk);

…

zk+ = ψk(х1, х2, … , хп; z1, z2, … , zk); y1 = ϕ1(х1, х2, … , хп; z1, z2, … , zk);

y2 = ϕ2(х1, х2, … , хп; z1, z2, … , zk);

…

ym = ϕm(х1, х2, … , хп; z1, z2, … , zk).

Эта модель называется булевым автоматом. Ее также можно представить в компактной векторной форме:

z+ = ψ(х, z); y = ϕ(х, z).

Булев автомат в определенном смысле ближе к реальным дискретным устройствам, поскольку его переменные непосредственно реализуются физическими переменными устройства, в частности, на типичных для современной техники элементах с двумя устойчивыми состояниями. Векторы х, у и z показывают структуру абстрактных символов а и b и состояния q. Приведенная выше система функций соответствует структуре, изображенной на рис. 22.2, где КС – комбинационная схема, реализующая приведенную выше систему, а П – блок памяти, осуществляющий задержку на период между соседними моментами времени.

Переменная zi представляет состояние i-го двоичного элемента памяти, а выражение

zi+ = ψi(х1, х2, … , хп; z1, z2, … , zk)

151

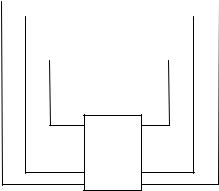
надо понимать так, что состояние i-го элемента памяти определяется значениями входных символов и состояниями элементов памяти в предыдущий момент времени.

…П …

Рис. 22.2. Структура булева автомата

152