
- •Дискретная математика
- •Минск 2015
- •1.1. Определения
- •1.2. Способы задания множеств
- •1.3. Операции над множествами
- •Рис. 1.1. Операции над множествами
- •2.1. Декартово произведение
- •2.3. Операции над бинарными отношениями
- •3.1. Абстрактный граф
- •3.2. Графическое представление бинарного отношения
- •Рис. 3.3. Представление композиции отношений: а) отношения R и S;
- •3.3. Матричные представления графа
- •4.1. Отношение изоморфизма
- •5.1. Цикломатическое число графа
- •6.1. Доминирующие множества графа
- •6.2. Независимые множества графа
- •7.1. Постановка задачи
- •8.1. Эйлеровы цепи и циклы
- •Рис. 8.3. Граф со взвешенными ребрами и выделенным кратчайшим путем
- •9.1. Определения
- •Рис. 9.1. Плоский граф
- •Рис. 9.2. Максимальный планарный граф
- •Рис. 9.3. Простейшие непланарные графы
- •10.1. Задачи подсчета
- •11.1. Постановка задачи
- •12.1. Способы задания булевой функции
- •Нормальные формы
- •14.1. Булев гиперкуб
- •Рис.14.1. Графическое представление булева пространства: а) одномерное; б) двумерное; в) трехмерное; г) четырехмерное
- •14.2. Представление булевых функций на гиперкубе
- •Рис.14.2. Трехмерный гиперкуб с заданной на нем булевой функцией
- •Рис.14.3. Графическое представление некоторых формул булевой алгебры: а) простое склеивание; б) простое поглощение; в) обобщенное склеивание
- •14.3. Развертка гиперкуба на плоскости. Карта Карно
- •Рис. 14.6. Зоны симметрии карты Карно
- •15.1. Функциональная полнота
- •15.2. Реализация булевых функций комбинационными схемами
- •16.1. Отношения на множестве троичных векторов. Операции над троичными векторами. Эквивалентность матриц
- •16.2. Эквивалентность матриц
- •16.3. Анализ троичной матрицы на вырожденность
- •17.1. Удаление избыточных элементарных конъюнкций
- •17.2. Удаление избыточных литералов
- •18.1. Метод Квайна-МакКласки
- •18.2. Метод Блейка-Порецкого
- •19.1. Постановка задачи
- •19.2. Применение метода Квайна-МакКласки
- •19.3. Минимизация слабо определенной функции
- •19.4. Расширение интервалов
- •20.1. Минимизация системы ДНФ
- •20.2. Минимизация системы слабо определенных булевых функций
- •21.1. Двухблочная разделительная декомпозиция
- •У т в е р ж д е н и е 21.3. Булева функция f (x) допускает параллельную разделительную декомпозицию вида (21.1) тогда и только тогда, когда она допускает двухблочные разделительные декомпозиции вида
- •21.4. Неразделительная декомпозиция
- •21.5. Декомпозиция систем булевых функций
- •22.1. Автомат с памятью
- •22.2. Представления автомата
- •22.3. Связь между моделями Мили и Мура
- •22.4. Автомат с абстрактным состоянием. Булев автомат
- •23.1. Эквивалентность состояний. Постановка задачи минимизации
- •23.2. Установление эквивалентности состояний
- •24.1. Отношение реализации. Постановка задачи минимизации
- •24.2. Совместимость состояний
- •24.3. Нахождение минимальной правильной группировки
- •Таблица 24.7
- •Таблица 24.9
- •Рис. 24.2. Дерево поиска минимальной правильной группировки
- •25.1. Задача кодирования состояний
- •25.2. Метод «желательных соседств»
- •26.1. Явление состязаний элементов памяти
- •26.2. Условие отсутствия опасных состязаний
- •26.3. Минимизация длины кода
- •26.4. Рассмотрение K-множеств
- •Литература
- •Матрица булева 15
- •Ядро 11

Граф ортогональности строк данной карты декомпозиции изображен на рис. 21.5, где вершины обозначены кодами соответствующих строк карты декомпозиции, а в скобках показана раскраска вершин графа – цвет «0» и цвет «1». Считая данные коды наборами значений аргументов х1, х2, х3 функции g, а величины в скобках – ее соответствующими значениями, получим
g(x1, x2, x3) = x2 x3 x1 x2 x2 x3.
000 (0) |
001 (1) |
011 (1) |
010 (1) |
101 (1) |
100 (0) |
111 (0) |
110 (1) |
Рис. 21.5. Граф ортогональности строк карты декомпозиции
По табл. 21.12, задающей функцию ϕ, получим ДНФ этой функции:
ϕ(g, x2, x4, x5) = g x2 x4 g x2 x4 g x4 x5 g x2 x5.
Многоблочные неразделительные декомпозиции получаются аналогично двухблочным неразделительным декомпозициям.
|
|
|
|
|
|
|
Таблица 21.12 |
|
|
|
Задание функции ϕ(g, x2, x4, x5) |
|
|
||||
g1 |
х2х4х5 |
|
|
|
|
|
|
|
0 0 0 |
0 0 1 |
0 1 0 |
0 1 1 |
1 0 0 |
1 0 1 |
1 1 0 |
1 1 1 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
21.5. Декомпозиция систем булевых функций
Рассмотрим следующую задачу. Пусть задана система не полностью определенных булевых функций f1, f2, … , fm от общего множества аргументов Х = {x1, x2, … , xn}. Для заданной пары подмножеств (Z1, Z2) множества Х, такой, что X = Z1 Z2, требуется найти суперпозиции
fi(x) = ϕi(g1(z1), g2(z1), … , gk(z1), z2), i = 1, 2, … , m, |
(21.2) |
где z1 и z1 – векторы, компонентами которых служат переменные из множеств Z1 и Z2, причем
k < |Z1 |, k + |Z2 | < n
139
ине важно, пересекаются или нет подмножества Z1 и Z2.
Ввекторной форме данную задачу сформулируем следующим образом: для системы функций y = f (x) требуется найти суперпозицию
y = ϕ(w, z2), w = g (z1),
такую, чтобы число компонент вектора w было меньше числа компонент вектора z1, а сумма чисел компонент векторов w и z2 была меньше длины вектора х. Дополнительно можно еще поставить задачу минимизации числа компонент вектора w.
Эта задача имеет приложение в синтезе логических схем из блоков, реализующих достаточно сложные системы булевых функций, с ограниченным числом внешних полюсов.
Для решения рассматриваемой задачи используется карта декомпозиции. Так же, как и для одной функции, строки ее соответствуют значениям векторной переменной z1, столбцы – значениям векторной переменной z2. На пересечении строки и столбца помещается значение вектора у (компоненты которого задают значения, которые принимают функции системы на соответствующих наборах значений аргументов). Ввиду неполной
определенности функций здесь не обязательно должно быть 2|Z1| строки и 2|Z2| столбца.
Каждую строку карты декомпозиции рассматриваем как троичный вектор, составленный из векторов значений функций.
У т в е р ж д е н и е 21.5. Система не полностью определенных булевых функций f1, f2, … , fm допускает декомпозицию в форме (21.2) тогда и только тогда, когда хроматическое число графа ортогональности строк ее карты декомпозиции для (Z1, Z2) не превышает 2k.
Если удастся раскрасить упомянутый граф в 2k цвета, то закодируем строки карты декомпозиции значениями векторной переменной
w = g (z1) = (g1(z1), g2(z1), … , gk(z1))
так, чтобы строки, соответствующие одноцветным вершинам, были закодированы одним кодом, а строки, соответствующие вершинам различных цветов, – различными кодами. Таким образом, значениям векторной переменной z1 ставятся в соответствие значения векторной переменной w, т. е. построена система функций g1(z1), g2(z1), … , gk(z1).
Карту декомпозиции, строкам которой приписаны значения переменной w, а столбцам – значения векторной переменной z2, можно рассматривать как
представление системы функций y = ϕ(w, z2).
Пусть, например, задана система слабо определенных булевых функций
у1 = f1(х), у2 = f2(х), у3 = f3(х),
140
где х = (x1, x2, х3, х4, х5, х6), и заданы векторные переменные
z1 = (x1, x2, х3, х4), z2 = {x5, x6}.
Заданная система представлена в виде пары булевых матриц, одна из которых содержит наборы значений аргументов (значения вектора х), другая представляет значения функций на этих наборах (значения вектора у). Считается, что на всех наборах значений аргументов, которые не присутствуют в соответствующей матрице, все функции заданной системы не определены. Матрицы имеют следующий вид:
х1 х2 х3 х4 х5 х6 |
|
у1 у2 |
у3 |
|
|||
1 0 0 |
0 |
0 |
0 |
|
0 1 1 |
1 |
|
|
0 |
1 |
|
|
|
|
2 |
0 1 0 |
1 |
|
0 1 0 |
||||
0 1 1 |
0 |
1 |
0 |
|
1 0 1 |
3 |
|
|
1 |
1 |
|
|
|
|
4 |
0 0 0 |
0 |
|
1 1 0 |
||||
1 0 0 |
0 |
0 |
1 |
, |
1 0 0 |
5 . |
|
|
0 |
1 |
|
|
|
|
6 |
1 1 1 |
0 |
|
0 1 1 |
||||
0 0 1 |
0 |
0 |
1 |
|
0 0 1 |
7 |
|
|
0 |
1 |
|
|
|
|
8 |
1 0 1 |
0 |
|
1 0 0 |
||||
0 0 0 |
1 |
0 |
1 |
|
1 0 1 |
9 |
|
|
0 |
0 |
|
|
|
|
10 |
0 1 1 |
0 |
|
0 0 1 |
||||
|
|
|
|
|
|
|
|
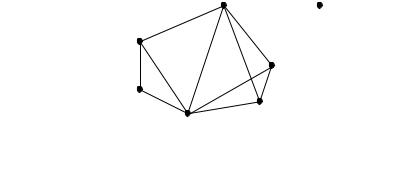
Карта декомпозиции системы булевых функций приведена в табл. 21.13. Граф ортогональности строк матрицы изображен на рис. 2.7. У вершин графа показаны наборы значений переменных x1, x2, x3, x4, которые приписаны соответствующим строкам карты декомпозиции.
0 1 1 0 (0 0) |
0 1 0 0 (0 0) |
1 0 0 0 (0 1) |
1 1 1 0 (0 1) |
|
0 0 1 0 (0 0) |
1 0 1 0 (1 1) |
0 0 0 1 (1 0) |
Рис. 21.6. Граф ортогональности строк карты декомпозиции |
141
Таблица 21.13
Карта декомпозиции системы слабо определенных булевых функций
у1 = f1 (х), у2 = f2 (х), у3 = f3 (х)
x1 x2 x3 x4 |
х5 x6 |
|
|
|
0 0 |
0 1 |
1 1 |
1 0 |
|
1 0 0 0 |
0 1 1 |
1 0 0 |
– – – |
– – – |
0 1 0 0 |
– – – |
– – – |
0 1 0 |
– – – |
0 1 1 0 |
0 0 1 |
– – – |
– – – |
1 0 1 |
0 0 0 1 |
– – – |
1 0 1 |
– – – |
1 1 0 |
1 1 1 0 |
– – – |
– – – |
– – – |
0 1 1 |
0 0 1 0 |
– – – |
0 0 1 |
– – – |
– – – |
1 0 1 0 |
– – – |
– – – |
– – – |
1 0 0 |
Граф раскрашивается не менее чем в четыре цвета, поскольку в нем легко заметен полный четырехвершинный подграф, все вершины которого должны быть раскрашены в разные цвета. В скобках приведены коды цветов в виде
двухкомпонентных булевых векторов w = (w1, w2). В то же время четыре цвета оказываются достаточными – в результате находится схема, показанная на рис. 21.7.
х1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
х2 |
|
|
|
w1 |
|
|
|
|
х3 |
|
|
|
|
|
|
y1 |
|
|
|
|
|
|||||
х4 |
|
|
|
w2 |
|
|
|
y2 |
|
|
|
|
|
||||
|
|
|
||||||
х5 |
|
|
|
|
|
|
y3 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
||
х6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Рис. 21.7. Схема, реализующая систему из трех функций от шести переменных
Систему функций w1 = g1(x1, x2, x3, x4), |
w2 = g2(x1, x2, x3, x4) представим |
||||||
следующими матрицами: |
|
|
|
|
|
|
|
х1 х2 |
х3 |
х4 |
|
w1 |
w2 |
|
|
1 0 |
0 |
0 |
|
0 |
1 |
1 |
|
|
0 |
|
|
|
|
2 |
|
0 1 |
0 |
|
0 |
0 |
|
||
0 1 |
1 |
0 |
, |
0 |
0 |
3 |
. |
|
0 |
|
|
|
|||
0 0 |
1 |
|
1 |
0 |
4 |
|
|
1 1 |
1 |
0 |
|
0 1 |
5 |
|
|
|
1 |
|
|
|
|
6 |
|
0 0 |
0 |
|
0 0 |
|
|||
|
1 |
|
|
|
|
7 |
|
1 0 |
0 |
|
1 1 |
|
|||
142
Табл. 21.14, полученную из табл. 21.13 совмещением неортогональных одноцветных строк, можно считать заданием системы функций y = ϕ(w, z2).
Таким образом, заданная система не полностью определенных булевых функций y = f (x) разложена на две системы:
w = g (z1) и y = ϕ(w, z2).
Последнюю представим парой матриц:
w1 w2 |
x5 |
x6 |
|
y1 y2 |
y3 |
|
0 1 |
0 |
0 |
|
0 1 1 |
1 |
|
|
1 |
|
|
|
|
2 |
0 0 |
1 |
|
0 1 0 |
|||
0 0 |
1 |
0 |
|
1 0 1 |
3 |
|
|
1 |
|
|
|
|
4 |
1 0 |
0 |
|
1 1 0 |
|||
0 1 |
0 |
1 |
, |
1 0 0 |
5 . |
|
|
1 |
|
|
|
|
6 |
0 1 |
0 |
|
0 1 1 |
|||
0 0 |
0 |
1 |
|
0 0 1 |
7 |
|
|
1 |
|
|
|
|
8 |
1 1 |
0 |
|
1 0 0 |
|||
1 0 |
0 |
1 |
|
1 0 1 |
9 |
|
|
0 |
|
|
|
|
10 |
0 0 |
0 |
|
0 0 1 |
|||
|
|
|
|
|
|
|
Таблица 21.14 Задание системы булевых функций y = ϕ(w, z2)
w1 w2 |
x5 x6 |
|
|
|
0 0 |
0 1 |
1 1 |
1 0 |
|
0 1 |
0 1 1 |
1 0 0 |
– – – |
0 1 1 |
0 0 |
0 0 1 |
0 0 1 |
0 1 0 |
1 0 1 |
1 0 |
– – – |
1 0 1 |
– – – |
1 1 0 |
1 1 |
– – – |
– – – |
– – – |
1 0 0 |
После минимизации получим следующие ДНФ:
w1 = x1 x2 x3 x4; w2 = x1;
y1 = w2 x5 x6 w1 w2 x6;
y2 = x5 x6 w1 w2 x6 w1 w2 x5; y3 = w1 x6 w2 x5.
143
