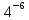- •Исходные данные:
- •Разработка алгоритма умножения
- •Умножение по алгоритму г
- •Синтез структуры сумматора-умножителя 2го типа
- •Минимизация функции п картами Вейча:
- •Минимизация функции картами Вейча:
- •Минимизация функции картами Карно:
- •Логический синтез одноразрядного четверичного умножителя-сумматора
- •Минимизация функции алгоритмом Квайна-МакКласке:
- •Минимизация функции картами Вейча:
- •Минимизация функции картами Карно:
- •Оценка эффективности минимизации переключательных функций
- •Синтез очс на основе мультиплексора
- •Логический синтез преобразователя множителя (пм)
Министерство образования Республики Беларусь
Учреждение образования
Белорусский государственный университет информатики и радиоэлектроники
Кафедра электронных вычислительных машин
Пояснительная записка к типовому расчету по дисциплине «Арифметические и логические основы вычислительной техники»
Тема: Разработка сумматора-умножителя
Выполнил: Германенко И.И.
Студент гр. 480562
MRY
Проверила:
Лукьянова И.В.
Минск 2015
Исходные данные:
Исходные
сомножители:
 = 81,92;
= 81,92;
 = 44,35;
= 44,35;
Алгоритм умножения: Г;
Метод умножения: умножение закодированного двоично-четверичного множимого на 2 разряда двоичного множителя одновременно в прямых кодах;
Варианты кодирования четверичных цифр двоичными кодами:
 =
10;
=
10;
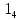 = 01;
= 01;
 = 11;
= 11;
 = 00;
= 00;
Тип синтезируемого умножителя: структурные схемы приведены для умножителя 2-го типа (ОЧС, ОЧУС, аккумулятор).
Метод минимизации ОЧС: карты Карно-Вейча.
Метод минимизации ОЧУС: Алгоритм Квайна-МакКласке, карты Карно-Вейча.
Функционально полный логический базис для схемы ОЧС (А4):
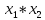

Логический базис для реализации ОЧС:

Функционально полный логический базис для схемы ОЧУС (А7):

Логический базис для реализации ОЧУС:

Арифметические операции сложения двоично-четверичных чисел с разными знаками в дополнительных кодах и умножения на 2 разряда множителя в прямых кодах должны выполняться одним цифровым устройством, именуемым сумматор-умножитель. Учитывая то, что суммирующие узлы обязательно входят в состав умножителя, начнем синтез с разработки алгоритма умножения.
Разработка алгоритма умножения
Перевод сомножителей из десятичной системы счисления в четверичную:
Множимое:

|
* |
0,92 4 |
|
* |
3,68 |
|
4 |
|
|
* |
2,72 4 |
|
|
2,88
|
 =1101,322
=1101,322
 =01011001,001111
=01011001,001111
Множитель:

|
* |
0,35 4 |
|
|
* |
1,40 |
|
|
|
4 |
|
|
* |
1,60 4 |
|
|
|
2,40
|
|
 =230,112
=230,112
 =110010,010111
=110010,010111
Запишем сомножители в форме с плавающей запятой в прямом коде:
Мн
= 0,010110010011  = 0.0110 (закодирован по заданию)
= 0.0110 (закодирован по заданию)
Мт
= 0,01010001111010  = 0.0011 (закодирован традиционно)
= 0.0011 (закодирован традиционно)
Умножение двух чисел с плавающей запятой на 2 разряда множителя одновременно в прямых кодах сводится к сложению порядков, формированию знака произведения, преобразованию разрядов множителя согласно алгоритму и перемножению мантисс сомножителей.
|
|
+4 |
|
|
|
+3 |
|
|
P = 0.0111 |
+7 |
|
Результат закодирован в соответствии с заданием на кодировку множимого.
Знак
произведения определяется суммой по
модулю двух знаков сомножителей: зн Мн
 зн Мт = 0 + 0 = 0
зн Мт = 0 + 0 = 0
Для
умножения мантисс необходимо предварительно
преобразовать множитель, чтобы исключить
диаду 11 (34),
заменив ее на триаду 1 и диаду 10 (24).
и диаду 10 (24).
Преобразованный множитель имеет вид:
 =1,
=1,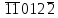
Мн = 0,110132 2Мн = 0,220330
 =
3,223202
=
3,223202  =
3,113010
=
3,113010
Умножение по алгоритму г
|
Четверичная с/с |
Двоично-четверичная с/с |
Комментарии |
||||||
|
0 |
000000 |
|
0 |
10 10 10 10 10 10 |
|
|
||
|
0 |
110132 |
|
0 |
01 01 10 01 00 11 |
|
|
||
|
0 |
110132 |
|
0 |
01 01 10 01 00 11 |
|
|
||
|
3 |
322320 |
2 |
1 |
00 11 11 00 11 10 |
11 |
|
||
|
0 |
033112 |
2 |
0 |
10 00 00 01 01 11 |
11 |
|
||
|
3 |
332232 |
02 |
1 |
00 00 11 11 00 11 |
10 11 |
|
||
|
0 |
032010 |
22 |
0 |
10 00 11 10 01 10 |
11 11 |
|
||
|
0 |
000000 |
000 |
0 |
10 10 10 10 10 10 |
10 10 10 |
|
||
|
0 |
032010 |
220 |
0 |
10 00 11 10 01 10 |
11 11 10 |
|
||
|
0 |
000011 |
0132 |
0 |
10 10 10 10 01 01 |
10 01 00 11 |
|
||
|
0 |
032021 |
2332 |
0 |
10 00 11 10 11 01 |
11 00 00 11 |
|
||
|
0 |
000002 |
20330 |
0 |
10 10 10 10 10 11 |
11 10 00 00 10 |
|
||
|
0 |
032030 |
10310 |
0 |
10 00 11 10 00 10 |
01 10 00 01 10 |
|
||
|
3 |
333333 |
113010 |
1 |
00 00 00 00 00 00 |
01 01 00 10 01 00 |
|
||
|
0 |
032023 |
222110 |
0 |
10 00 11 10 11 00 |
11 11 11 01 01 10 |
|
||
После
окончания умножения необходимо оценить
погрешность вычислений. Для этого
полученное произведение
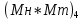 =
0,032023222110
приводится
к нулевому порядку (
=
0,032023222110
приводится
к нулевому порядку ( *
* 7),
а затем переводится в десятичную систему
счисления:
7),
а затем переводится в десятичную систему
счисления:
 =
320232,22110
=
320232,22110
 =
3630,64453125
=
3630,64453125
Результат прямого перемножения операндов дает следующее значение:
 =
3633,15185547
=
3633,15185547
Абсолютная погрешность:
Δ = 3633,15185547 - 3630,64453125 = 2,50732422
δ ;
δ =
;
δ =

Эта погрешность получена за счет приближенного перевода из десятичной системы счисления в четверичную обоих сомножителей, а также за счет округления полученного результата произведения.

 =
0.0100
=
0.0100
 =
0.0011
=
0.0011

 =Мн*
=Мн*

 =
= *
*

 =
= *
*

 =0*Мн*
=0*Мн*

 =
= *
*

 =
= *
*

 =
= *
*