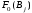Задача 10
По выборке одномерной случайной величины:
- получить вариационный ряд;
- построить на масштабно-координатной бумаге формата А4 график эмпирической функции распределения F*(x);
- построить гистограмму равноинтервальным способом;
- построить гистограмму равновероятностным способом;
- вычислить точечные оценки математического ожидания и дисперсии;
- вычислить интервальные оценки математического ожидания и дисперсии (γ = 0,95);
- выдвинуть гипотезу о законе распределения случайной величины и проверить ее при помощи критерия согласия 2 и критерия Колмогорова ( = 0,05). График гипотетической функции распределения F0(x) построить совместно с графиком F*(x) в той же системе координат и на том же листе.
Решение:
Построим
график эмпирической
функции распределения
 (рис. 10.1).
(рис. 10.1).
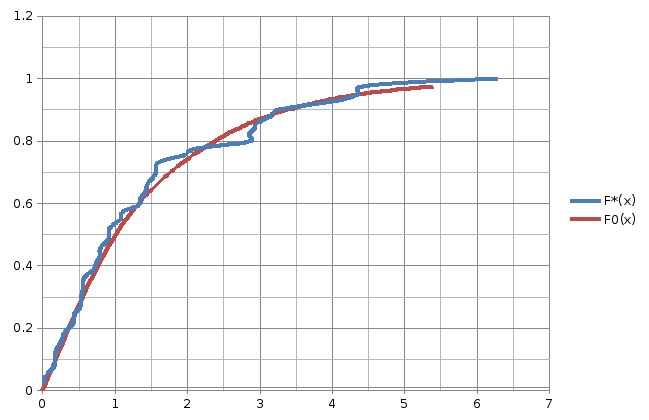
Рис.
10.1 Графики эмпирической
 и гипотетической функций распределения
F0(x).
и гипотетической функций распределения
F0(x).
Количество интервалов M, необходимое для построения гистограмм, определим по объему выборки:

Для равноинтервальной гистограммы величины hj, Aj, Bj, рассчитаем и заполним все колонки интервального статистического ряда (таб. 10.1):
Таблица 10.1
|
j |
Aj |
Bj |
hj |
j |
|
|
|
1 |
0,03 |
0,924 |
0,894 |
26 |
0,5306 |
0,5933 |
|
2 |
0,924 |
1,819 |
0,894 |
14 |
0,2857 |
0,3195 |
|
3 |
1,819 |
2,713 |
0,894 |
4 |
0,0816 |
0,0913 |
|
4 |
2,713 |
3,607 |
0,894 |
2 |
0,0408 |
0,0456 |
|
5 |
3,607 |
4,501 |
0,894 |
1 |
0,0204 |
0,0228 |
|
6 |
4,501 |
5,396 |
0,894 |
1 |
0,0204 |
0,0228 |
|
7 |
5,396 |
6,290 |
0,894 |
1 |
0,0204 |
0,0228 |
Равноинтервальная гистограмма имеет вид, согласно рис. 10.2:


Рис. 10.2 Равноинтервальная гистограмма
Для
равновероятностной
гистограммы
величины j
, ,
Aj,
Bj,
рассчитаем и заполним все колонки
интервального статистического ряда
(таб. 10.2):
,
Aj,
Bj,
рассчитаем и заполним все колонки
интервального статистического ряда
(таб. 10.2):
Таблица 10.2
|
j |
Aj |
Bj |
hi |
j |
|
|
|
1 |
0,03 |
0,245 |
0,215 |
7 |
0,143 |
0,6645 |
|
2 |
0,245 |
0,535 |
0,29 |
7 |
0,143 |
0,4926 |
|
3 |
0,535 |
0,79 |
0,255 |
7 |
0,143 |
0,5602 |
|
4 |
0,79 |
1,21 |
0,42 |
7 |
0,143 |
0,3401 |
|
5 |
1,21 |
1,61 |
0,4 |
7 |
0,143 |
0,3571 |
|
6 |
1,61 |
3,06 |
1,45 |
7 |
0,143 |
0,0985 |
|
7 |
3,06 |
6,29 |
3,23 |
7 |
0,143 |
0,0442 |
Равновероятностная гистограмма имеет вид, согласно рис. 10.3:

Рис. 10.3 Равновероятностная гистограмма
Вычислим точечную оценку математического ожидания:

Вычислим точечную оценку дисперсии:

Построим
доверительный
интервал для математического ожидания
с надежностью γ = 0,95. Для этого в таблице
функции Лапласа найдем значение, равное
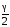 = 0,475, и определим значение аргумента,
ему соответствующее:
= 0,475, и определим значение аргумента,
ему соответствующее:
 .
Затем вычислим
.
Затем вычислим
 и получим доверительный интервал для
математического ожидания:
и получим доверительный интервал для
математического ожидания:
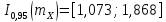
Построим доверительный интервал для дисперсии с надежностью γ = 0,95. Вычислим

и получим доверительный интервал для дисперсии:
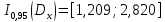
По
виду графика эмпирической функции
распределения
 и гистограмм выдвигаем двухальтернативную
гипотезу о законе распределения случайной
величины
и гистограмм выдвигаем двухальтернативную
гипотезу о законе распределения случайной
величины
 – величина
X
распределена по экспоненциальному
закону:
– величина
X
распределена по экспоненциальному
закону:


 – величина
X
не распределена по нормальному закону:
– величина
X
не распределена по нормальному закону:

Оценку неизвестного параметра экспоненциального распределения можно определить по формуле

Проверим
гипотезу об экспоненциальном законе с
помощью критерия
 .
.
Вычислим
значение
критерия
 на
основе
равноинтервального
статистического
ряда:
на
основе
равноинтервального
статистического
ряда:

Теоретические вероятности pj попадания в интервалы равноинтервального статистического ряда нормальной случайной величины вычислим по формуле:

Результаты расчета можно свести в таблицу:
Таблица 10.3
|
j |
Aj |
Bj |
|
|
|
|
|
|
1 |
0,000 |
0,894 |
0 |
0,455618 |
0,4567 |
0,5306 |
0,012344 |
|
2 |
0,924 |
1,819 |
0,466611 |
0,709633 |
0,2531 |
0,2857 |
0,0075 |
|
3 |
1,819 |
2,713 |
0,709633 |
0,841929 |
0,1323 |
0,0816 |
0,019402 |
|
4 |
2,713 |
3,607 |
0,841929 |
0,913949 |
0,0721 |
0,0408 |
0,013519 |
|
5 |
3,607 |
4,501 |
0,913949 |
0,953155 |
0,0393 |
0,0204 |
0,009013 |
|
6 |
4,501 |
5,396 |
0,953155 |
0,974499 |
0,0274 |
0,0204 |
4,1E-05 |
|
7 |
5,396 |
6,290 |
0,974499 |
0,986118 |
0,0117 |
0,0204 |
0,006649 |
|
|
|
|
|
Сумма: |
0,9926 |
1 |
0,068468 |
Проверяем
выполнение контрольного соотношения
для
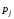 :
:

В
результате получаем

Вычислим
число степеней свободы k=M-1-s=7-1-1=5
и по заданному уровню значимости
=0,05 из таблицы распределения
 выбираем критическое значение
выбираем критическое значение

Так
как
 то гипотеза
то гипотеза
 об экспоненциальном законе распределения
принимается (нет основания ее отклонить).
об экспоненциальном законе распределения
принимается (нет основания ее отклонить).
Проверим
гипотезу об экспоненциальном законе
распределения с помощью критерия
Колмогорова. Построим
график
 в одной системе координат с графиком
эмпирической функции распределения
в одной системе координат с графиком
эмпирической функции распределения
 (см. рис 10.1). В качестве опорных точек
для графика
(см. рис 10.1). В качестве опорных точек
для графика
 используем
10 значений
используем
10 значений
 из
таб. 10.3.
из
таб. 10.3.
По
графику определим максимальное по
модулю отклонение между функциями
 и
и
 :
:

Z=0,05
Вычислим значение критерия Колмогорова:

Из
таблицы Колмогорова по заданному уровню
значимости
=0,05 выбираем критическое значение

Так
как
 ,
то гипотезу
,
то гипотезу
 об экспоненциальном законе распределения
отвергать нет основания.
об экспоненциальном законе распределения
отвергать нет основания.