
Задача № 1.3
Подбрасываются две игральные кости. Определить вероятность того, что сумма выпавших чисел превышает 10.
Решение.
Всего возможно n2=62=36 исходов опыта.
Сумма выпавших чисел превышает 10 в следующих случаях: 6 и 5, 5 и 6, 6 и 6.
Т.е. число благоприятствующих исходов m=3. Вероятность того, что сумма выпавших чисел превышает 10 равна:

Ответ: р=0,0833.
Задача 2.27
Приведена схема соединения элементов, образующих цепь с одним входом и одним выходом. Предполагается, что отказы элементов являются независимыми в совокупности событиями. Отказ любого из элементов приводит к прерыванию сигнала в той ветви цепи, где находится данный элемент. Вероятности отказа элементов 1, 2, 3, 4, 5 соответственно равны q1=0,1; q2=0,2; q3=0,3; q4=0,4; q5=0,5. Найти вероятность того, что сигнал пройдет со входа на выход.

Решение:

Опишем через события работу элементов цепи. Пусть событие А1 состоит в том, что работает элемент 1, событие А2 – элемент 2, событие А3 – элемент 3, событие А4 – элемент 4, событие А5 – элемент 5.
Тогда вероятность этих событий запишется так:
р(А1)=р1=1-q1=1-0,1=0,9;
р(А2)=р2=1-q2=1-0,2=0,8;
р(А3)=р3=1-q3=1-0,3=0,7;
р(А4)=р4=1-q4=1-0,4=0,6;
р(А5)=р5=1-q5=1-0,5=0,5.
Вероятности противоположных событий (т.е. того, что элементы 1, 2, 3 не работают) даны в условии:

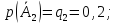



Анализируем заданную цепь и определяем участки с последовательным и параллельным соединением.
Элементы 1, 2 и 3 соединены параллельно. Введем событие В, состоящее в том, что ток пройдет из точки 1 в точку 2; это произойдет тогда, когда будет работать или элемент 1, или элемент 2, или элемент 3. Можно записать В=А1+А2+А3.
Элементы 4 и 5 соединены параллельно. Введем событие С, состоящее в том, что ток пройдет из точки 2 в точку 3; это произойдет тогда, когда будут работать или элемент 4, или элемент 4. Тогда событие С можно записать С=А4+А5. Рассмотрим событие D состоящее в том, что ток пройдет из точки 1 в точку 3, оно выполнится тогда, года выполнится и событие В и событие С. Событие D запишется так: D=В∙С. По условию задачи необходимо найти вероятность события D.
p(D)=р(В∙С)=р(В)∙р(С). (2.1)
Найдем вероятности, входящие в правую часть формулы (2.1):
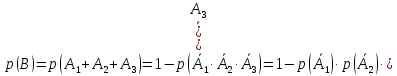
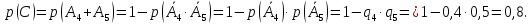
Подставляя полученные значения в формулу (2.1), получим:
р(D)=р(В)∙р(С)=0,994∙0,8=0,7952.
Ответ: р(D)=0,7952.
Задача 3.26.
Имеются три одинаковых по виду ящика. В первом ящике 20 белых шаров, во втором - 10 белых и 10 черных шаров, в третьем - 20 черных шаров. Из выбранного наугад ящика вынули шар. Вычислить вероятность того, что шар белый.
Решение:
Обозначим через А событие, что достали белый шар.
Общее число шаров равно 60.
Обозначим:
р=20/60=0, 333 –

р=20/60=0, 333 –

р=20/60=0, 333 –
Выдвигаем гипотезы:
Н1 – достали белый шар из первой коробки. Это белый шар.
Вероятность данной гипотезы: р(Н1)=р1∙1=0,333.
Н2 – достали шар из второй коробки. Это белый шар.
Вероятность
данной гипотезы:

Н3 – достали шар из второй коробки. Это черный шар.
Вероятность
данной гипотезы:

Н4 – достали шар из третьей коробки. Это серный шар.
Вероятность
данной гипотезы:
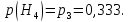
Событие А однозначно произойдет при гипотезах Н1 и Н2, и не произойдет в остальных случаях. Следовательно условные вероятности события А равны:
р(А|Н1)= р(А|Н2)=1
р(А|Н3)= р(А|Н4)=0
По формуле полной вероятности найдем вероятность события А:


Ответ: р(А)=0,4995.
Задача 4.28
Вероятность того, что данный баскетболист забросит мяч в корзину, равна 0,9. Произведено 12 бросков. Найти вероятность того, что будет не менее 11 попаданий.
Решение:
Введем событие А – баскетболист забросит мяч в корзину.
Вероятность того, что при n=12 независимых испытаниях событие А появится не менее m=11 раз, вычислим по формуле:



=

Ответ: 0,6904.
Задача 5.20
Дискретная случайная величина Х может принимать одно из пяти фиксированных значений x1, x2, x3, x4, x5 с вероятностями p1, p2, p3, p4, p5 соответственно (значения приведены в таб. 5.1). Вычислить математическое ожидание и дисперсию величины Х. Рассчитать и построить график функции распределения.
Таблица. 5.1
|
Вариант |
x1 |
x2 |
x3 |
x4 |
x5 |
p1 |
p2 |
p3 |
p4 |
p5 |
|
5.20 |
5 |
6 |
7 |
8 |
9 |
0,1 |
0,1 |
0,1 |
0,1 |
0,6 |
Решение.
|
|
5 |
6 |
7 |
8 |
9 |
|
|
0,1 |
0,1 |
0,1 |
0,1 |
0,6 |
Рассчитаем
значения функции распределения для
фиксированных значений
 ,
взятых из ряда распределения.
,
взятых из ряда распределения.
Для Х1=5;

Для Х2=6;

Для Х3=7;
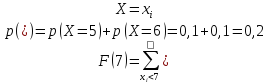
Для Х4=8;
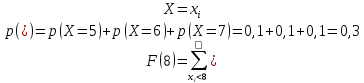
Для Х5=9;

Для
Х6= ;
согласно свойствам функции распределения
;
согласно свойствам функции распределения
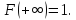

Вычислим математическое ожидание дискретной СВ Х:
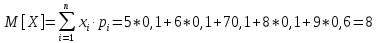
Вычислим дисперсию дискретной СВ Х:
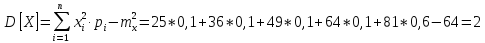
Задача 6.21
Случайная величина Х задана плотностью вероятности


Определить
константу С,
математическое ожидание, дисперсию,
функцию распределения величины Х,
а также вероятность ее попадания в
интервал .
.
Таблица 6.1
|
Вариант |
|
a |
b |
|
|
|
6.21 |
c x9 |
0 |
1 |
0 |
0,25 |
Решение:
Вычислим значение константы с из условия нормироввки.

Из условия нормировки следует:

Плотность вероятности примет вид:
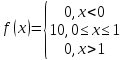
Определим функцию распределения F(x). Так как плотность вероятности задана разлисными формулами на разных интервалвх, то и ее первообразную – функцию распределения – будем искать для каждого интервала в отдельности.
Для x<0;

Для
 ;
;

Для
 ;
;

Окончательно имеем:

Вычислим
вероятность

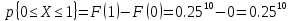
Вычислим математическое ожидание
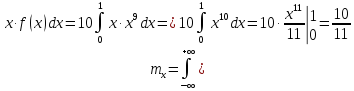
Вычислим димперсию:

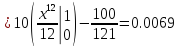



 x,c)
x,c)