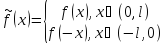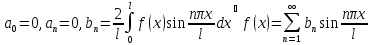- •12. Ряд Тейлора. Критерий разложимости функции в ряд Тейлора.
- •1. Числовые ряды. Основные понятия. Действия над рядами. Необходимое условие сходимости ряда
- •2. Интегральный признак сходимости рядов с неотрицательными членами
- •3. Признаки сравнения для рядов с неотрицательными членами
- •4. Признак Даламбера для рядов с неотрицательными членами
- •5. Признак Коши для рядов с неотрицательными членами
- •6. Знакочередующиеся ряды. Признак Лейбница
- •7. Знакопеременные ряды, ряды с комплексными членами. Абсолютная и условная сходимость. Свойства абсолютно и условно сходящихся рядов
- •8. Равномерная сходимость функционального ряда. Признак Вейерштрасса равномерной сходимости
- •9. Свойства равномерно сходящихся функциональных рядов: теоремы о непрерывности суммы, о почленном дифференцировании и почленном интегрировании
- •10.1 Степенные ряды. Теорема Абеля. Радиус и интервал (круг) сходимости степенного ряда
- •15.Основные элементарные функции комплексной переменной
- •16. Производная функции комплексной переменной. Условия Коши-Римана. Аналитические функции. Действительная и мнимая части аналитической функции
- •17. Интеграл от функции комплексной переменной, его вычисление и свойства
- •18. Интегральная теорема Коши. Первообразная и интеграл аналитической функции
- •18. Интегральная теорема Коши. Первообразная и интеграл аналитической функции
- •19.Интегральная формула Коши. Теорема о производных аналитической функции
- •20. Ряды в комплексной области. Свойства функциональных рядов. Степенные ряды
- •21. Ряд Тейлора для функции комплексной переменной. Ряд Лорана
- •22. Нули и изолированные особые точки аналитических функций. Классификация изолированных особых точек
- •23. Понятие вычета. Основная теорема о вычетах
- •24. Вычисление вычетов
- •25. Вычисление интегралов вида,с помощью вычетов
- •26. Скалярное произведение функций. Норма функции. Ортогональные системы функций. Основная тригонометрическая система функций
- •27. Ряды Фурье по ортогональным системам функций
- •28. Сходимость в среднем функционального ряда. Связь между различными видами сходимости. Экстремальное свойство коэффициентов ряда Фурье
- •29. Неравенство Бесселя. Равенство Парсеваля-Стеклова. Полнота и замкнутость ортогональной системы функций
- •30. Тригонометрические ряды Фурье для периодических функций. Признак сходимости тригонометрического ряда Фурье (теорема Дирихле)
- •31. Разложение непериодических функций в тригонометрический ряд Фурье. Ряд Фурье только по косинусам или только по синусам
- •32. Комплексная форма тригонометрического ряда Фурье. Понятие о спектре
- •33. Интеграл Фурье. Комплексная форма интеграла Фурье
- •34. Преобразования Фурье. Косинус- и синус- преобразования Фурье
- •35. Преобразование Лапласа, оригинал и изображение. Основные теоремы операционного исчисления
- •36. Приложение операционного метода к решению дифференциальных уравнений и систем дифференциальных уравнений
29. Неравенство Бесселя. Равенство Парсеваля-Стеклова. Полнота и замкнутость ортогональной системы функций
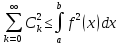 и
и
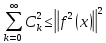 – неравенство
Бесселя
– неравенство
Бесселя
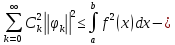 для
ортогональных систем
для
ортогональных систем
4)(?)
f(x) L2[a,
b] , f(x)~
L2[a,
b] , f(x)~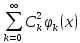 ,
Ck=
,
Ck=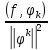
T
Для того,
чтобы обобщенный ряд Фурье
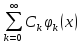 – сходился в среднем к функцииf(x)
на отрезке [a,
b],
необходимо и достаточно, чтобы неравенство
Бесселя обращалось для f(x)
в равенство, т.е.
– сходился в среднем к функцииf(x)
на отрезке [a,
b],
необходимо и достаточно, чтобы неравенство
Бесселя обращалось для f(x)
в равенство, т.е.
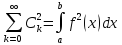 и
и

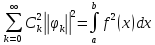
Доказательство:
Ряд
 сходится в среднем на [a,
b],
если
сходится в среднем на [a,
b],
если
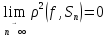
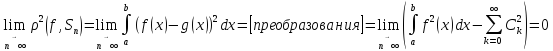 ,
,
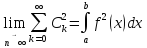
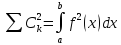 –равенство
Парсеваля – Стеклова
–равенство
Парсеваля – Стеклова
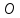 .
Ортогональная
система функций (
.
Ортогональная
система функций (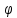 0,
0,
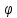 1,
1,
 2,
…,
2,
…,
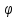 n)
в пространстве L2[a,
b]
называются полной, если для
n)
в пространстве L2[a,
b]
называются полной, если для
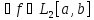 выполняется равенство Парсеваля-Стеклова
выполняется равенство Парсеваля-Стеклова
E3
– Евклидово 3хмерное пространство, E3(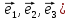 – ортонормированный базис |ei
| = 1
– ортонормированный базис |ei
| = 1
 ,
,
 ,
,
 –теорема Пифагора
для пространства E3.
–теорема Пифагора
для пространства E3.
В ортонормированном
базисе ||f||2=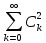 – теорема Пифагора в бесконечномерном
пространстве.
– теорема Пифагора в бесконечномерном
пространстве.
Вывод: Любая функция f(x) принадлежащая пространству L2[a, b] может быть разложена в сходящийся к ней в среднем ряд Фурье по ортогональной на отрезке [a,b] системе функций, если эта система является полной в пространстве L2[a, b].
30. Тригонометрические ряды Фурье для периодических функций. Признак сходимости тригонометрического ряда Фурье (теорема Дирихле)
Пусть f(x) кусочно непрерывная функция, периодичная с периодом T=2l , [-l,l]
Пример:
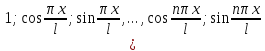 ),
где ||1||=
),
где ||1||=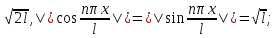
f(x)~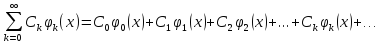
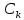 =
=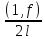 =
=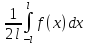

(солнышко)
О. Тригонометрический
ряд
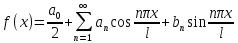 ,
коэффициенты которого определены по
формулам (солнышко) называется
тригонометрическим для периодичной
функции f(x)
,
коэффициенты которого определены по
формулам (солнышко) называется
тригонометрическим для периодичной
функции f(x)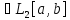 .
.
Если f(x) четная, то
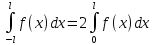 ,
если нечетная, то
,
если нечетная, то
Если f(x) – четная, то
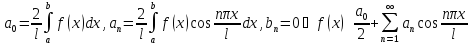
Если f(x) - нечетная, то

Уравнение Ляпунова
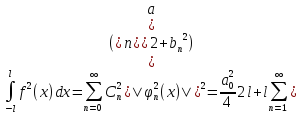
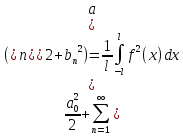
Т.
основная тригонометрическая система
функций является полной в пространстве
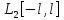 .
.
 -
число ⇒
-
число ⇒
 сходитcя
⇒ a→ 0, n→
сходитcя
⇒ a→ 0, n→
 ,b→
0, n→
,b→
0, n→
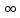
Признаки сходимости тригонометрических рядов Фурье
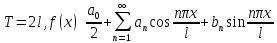
кусочно-непрерывная функция f(x) называется кусочно-гладкой на [a,b], если её производная имеет конечное число точек разрыва 1 рода и существует правосторонняя производная в точке A и левосторонняя в точке B.

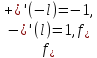
T1
Если функция f(x)
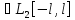 т. е она кусочно-непрерывна на[-l,
l], то
тригонометрический ряд Фурье сходится
к f(x) в среднем.
т. е она кусочно-непрерывна на[-l,
l], то
тригонометрический ряд Фурье сходится
к f(x) в среднем.
Т2 (Дирихле)
Если f(x)
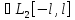 является кусочно гладкой на [-l,
l],
то её тригонометрический ряд Фурье
сходится в каждой точке этого отрезка
для суммы S(x) ряда Фурье :
является кусочно гладкой на [-l,
l],
то её тригонометрический ряд Фурье
сходится в каждой точке этого отрезка
для суммы S(x) ряда Фурье :
S(x) = f(x), если x - точка непрерывности функции f(x)
S(
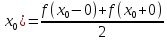 ,
если
,
если точка
разрыва 1 рода функции f(x)
точка
разрыва 1 рода функции f(x)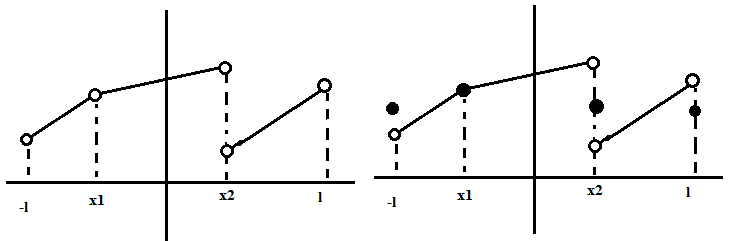
S(-l) = S(l)=
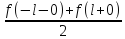
T3 Если функция
f(x)
 яфляется кусочно гладкой и непрерывной
на [-l, l]
и f(l)=f(-l), то и тригонометрический ряд
Фурье сходится к f(x) на [-l,
l] равномерно.
яфляется кусочно гладкой и непрерывной
на [-l, l]
и f(l)=f(-l), то и тригонометрический ряд
Фурье сходится к f(x) на [-l,
l] равномерно.
Разложение в ряд
Фурье четных и нечетных ф-ций на интервале
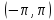 .
.
Пусть функция f(x) – четная, т. е. f(-x)=f(x).
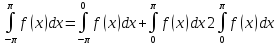
Значит:
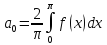 ;
;
Ряд Фурье для
четных функций – ряд только по косинусам:

Пусть функция f(x) – нечетная, т. е. f(-x)=-f(x).
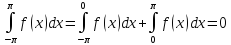
Значит:
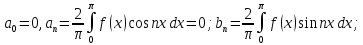
Ряд Фурье для
нечетных функций – ряд только по синусам.
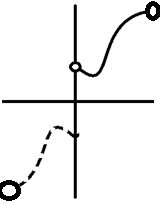
31. Разложение непериодических функций в тригонометрический ряд Фурье. Ряд Фурье только по косинусам или только по синусам
f(x) – непериодичная функция
Вместо функции
f(x)
рассматривают функцию f*(x)
с периодом 2l,
причем [a,
b] [-l,
l]
и на [a,
b]
функция f*(x)
совпадает с функцией f(x).
[-l,
l]
и на [a,
b]
функция f*(x)
совпадает с функцией f(x).
Поскольку функция f*(x) –периодическая, то её разлагают в ряд Фурье.
Рассмотрим один
важный случай, пусть функция f(x)
задана на интервале (0, l).
Её надо доопределить на интервале (-l,
0). Можно это сделать двумя способами:
четным и нечетным. В первом случае мы
получаем ряд Фурье только по косинусам,
во втором – только по синусам. 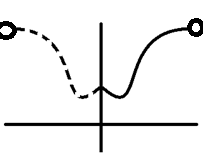
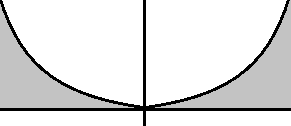
1) Пусть f(x) задана на (0, l). Доопределим её четным образом. Функция будет выглядеть так:
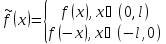
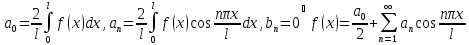
Пусть
f(x)
задана на (0, l).
Доопределим её четным образом. Функция
будет выглядеть так: