24. Вычисление вычетов

1. Z=Z₀ – ноль k-порядка ф-ции f(z)

C_-1 = 0, res _Z=Z0 f(z) = 0

2. Z=Z₀ – УОТ ф-ции f(z)

C_-1 = 0, res _Z=Z0 f(z) = 0

3. Z=Z₀ –простой полюс ф-ции f(z)

f(Z)(Z - Z₀) = C_-1 + С₀(Z - Z₀) + С₁(Z - Z₀)^2+…

(C_-1 + С₀(Z - Z₀) + С₁(Z - Z₀)^2+..) = C_-1

res _Z=Z0 f(z) =

Важный частный случай:

Пусть .

Z = Z₀ – простой полюс f(z)

φ(Z₀) не = 0, ψ(Z₀) = 0, ψ’(Z₀) не = 0

res _{Z = Z0} f(z) .

4. Z=Z₀ –полюс k-го порядка ф-ции f(z)

res _{Z = Z0} f(z)

5. Z=Z₀ –COT ф-ции f(z)

res _Z=Z0 f(z) = C_-1

25. Вычисление интегралов вида,с помощью вычетов

Замена z=e^it

, =

R→∞ ;

; ;

R(x) – правильная рац. дробь ; λ>0; λR

Вычисление интегралов с помощью вычетов

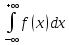
; ; n≥m*2

F(x) непрерывна на ()

Лемма Жердана. Пусть g(z) - аналитическая ф–ция в верхней плоскости за искл. конечного числа особых точек и стремится в этой полуплоскости к нулю, при тогда при>0

26. Скалярное произведение функций. Норма функции. Ортогональные системы функций. Основная тригонометрическая система функций

Ортогональная система функций

f(x) x₀ Р. – Тейлора Ǝ f⁽ⁿ⁾(x), n N;

О. f(x) наз-ся. кусочно-непрерывной на [a,b] , если она непрерывна во всех точках этого отрезка, за исключением точки разрыва l рода.

f(x) – кусочно-непрерывна → Ǝ

Ǝ

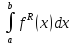
Мн-во всех кусочно непрерывных функций – ϕ(x),ψ(x) на [a,b]

(ϕ,ψ)= (елочка)

1. (ϕ,ψ)= (ψ, ϕ)

2. (ϕ₁+ ϕ₂,ψ)=( ϕ_1,ψ)+ (ϕ₂,ψ)

3. (λ ϕ,ψ)= λ (ϕ,ψ),

4. (ϕ, ϕ)≥0, В (ϕ, ϕ)=0 в т. непрерывности

Мно-во всех кусочно-непрерывных на [a,b] функций со скалярным произведением (елочка) наз. пространства L₂ [a,b]

||ϕ|| =

||ϕ|| =1, то функция наз. Нормированной

Определение: ϕ(x) и ψ(x) наз. L₂[a,b] наз. Ортогональным на [a,b],если

(ϕ_в,ψ)=0 ;

О. Система функций ϕ₁,ϕ_2.. ϕ_n (конечно или бесконечное) наз. Ортогональной на отр. [a,b],если все функции этой системы попарно ортог. На отр. [a,b],

О. Ортогональная система функций (ϕ₁,ϕ_2.. ϕ_n) на отр. [a,b], наз. Ортонормированной, если ||ϕ_n²||=( ϕ_n, ϕ_n)=

Основная тригонометрическая система функций

(1, ,…,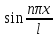)(вишенка)

Т. Основная тригонометрическая сист. (вишенка) явл. ортогональной на любом отрезке длины = 2L ,причем ;

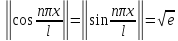для .

Док-во:

;

Док-во:

= ½

; =

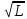
Другие ортогональные системы функций

Ортог. Сист.функций	Отрезок отрг.	Нормы эл-тов
(	[0;1]	||1||=;
(	[0;1]

27. Ряды Фурье по ортогональным системам функций

() (*) – ортогональная система функций в

-обобщ. Ряд Фурье по ортогональной системе *

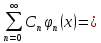Пусть ряд сх. к ф-цииg(x) ∈ , т. е. g(x)

Предположим, что ряд сх. равномерно, т. е. его можно инт-ть почленно

+

)=

, V n=0, 1, 2,…

Пусть дана некоторая ф-ция f(x) ∈ . Формально выч-лим коэф. ,

Пусть (,) – базис в пр-ве=+

, i=1, 2, 3,…

-мерное пр-во

28. Сходимость в среднем функционального ряда. Связь между различными видами сходимости. Экстремальное свойство коэффициентов ряда Фурье

Дано: f(x) и g(x) на [a,b].

max | f(x) – g(x) |, x[a,b]

–среднее квадратичное уклонение

f,gL₂[a,b]

(f , g ) =

Виды сходимости:

1) Поточечная сходимость (где-то ранее)

2) Равномерная сходимость (там же) 3) Сходимость в среднем.

3) (?) функциональный ряд, S_n(x) = U₀(x)+…+ U_n(x), функциональный ряд называется сходящимся в среднем к функцииf(x) на [a,b], если

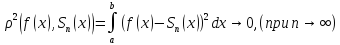
// - сходиться в среднем к функции f(x).

T Если функциональный ряд на отрезке [a,b] сходится равномерно к функции f(x), то он сходится и в среднем к функции f(x).

Доказательство:

Если функциональный ряд на отрезке [a, b] сходится равномерно к функции f(x), т.е. >0x[a,b], N=N(),n>N()|f(x) – S_n(x) | < , тогда, т.е.

Обратное утверждение неверно!

Экстремальные свойства Коэффициентов Фурье.

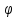Ортонормированные системы функций (­₀, ­₁, ­₂, …, ­_n, …) и f(x)L₂[a, b], nN

Зафиксируем S_n(x)=

Как подобрать , чтобы среднее квадратичное уклонение(f , S_n ) было минимальным?

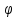( f , S_n )= || f(x) – S_n(x)||²=_k=C_k=(f,_k) (_k=C_k=

Теорема об экстремальном свойстве коэффициентов Фурье:

Среди всех обобщенных многочленов вида S_n(x) =средней квадратичной аппроксимации функцииf(x) является многочлен Фурье, т.к. такой многочлен коэффициенты которого находятся по указанным формулам.

Многочлен S­­_n(x) аппроксимирует функция f(x) в среднем (в смысле метода наименьшего квадрата).

Доказательство: (f,S_n)=-,min²(f,S_n)0,() неутыв(неразборчиво) и огранич. Сверху– сходится (см след вопрос)
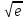