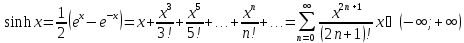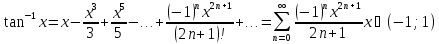8. Равномерная сходимость функционального ряда. Признак Вейерштрасса равномерной сходимости

Пусть u₁(x), u₂(x),…,u_n(x)-послед. Функций, определенных на некотором мн-ве. X.

О:Ряд вида u₁(x)+ u₂(x)+…+u_n(x)+…=наз-сяфункциональным рядом при х₀ ∈ Х

–числовой ряд, х₀ – точка сходимости. Множество всех точек сходимости наз. областью сходимости функционального ряда

Д-область сх-ти функционального ряда. Д Х

Sn(х) = u₁(x)+ u₂(x)+…+u_n(x) = -n-ая частичная сумма функционального ряда

S(x) = , опред. в области Д, наз-ся суммой функционального ряда

r_n(x) = S(x) – S_n(x), опред. в обл. Д наз. n-ым остатком функционального ряда

r_n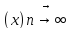0, Vx∈Д

Сходимость функционального ряда в каждой т x∈Д наз-ся поточечной сходимостью функционального ряда.

Функциональны ряд наз-ся абсол. сходящ на мн-ве Д₁Х, если в каждой точке x∈Д ряд

Сход., Д₁Д

Равномерная сх-ть функционального ряда

Поточечн сх-ть Vɛ>0 Vx∈Д∃ N = N(ɛ,х), Vn≥N(ɛ,x) =>|Sn(x)-S(x)|<ɛ

О: Функц. Ряд наз равновмерн сход к функции S(x) на мн-ве Д, если

Vɛ>0 Vx∈Д∃ N = N(ɛ), Vn≥N(ɛ)=>|Sn(x)-S(x)|<ɛ

Sn(x)S(x)

О: Числовой ряд 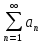назыв мажорантой для функц. Рядана мн-ве Д, если вып-ся :

1. |u_n(x)| ≤a_n, Vn ∈N, Vx ∈Д

2. cx.

Теор/признак Вейерштрасе:Если у функц. Ряда на мн-ве Д∃ мажоранта, то функц ряд на мн-ве Д сход равномерно и абсолютно.

Замечание: призн Вейерштрасе явл-ся лишь достат. Усл для равн сход ряда.

9. Свойства равномерно сходящихся функциональных рядов: теоремы о непрерывности суммы, о почленном дифференцировании и почленном интегрировании

= S(x) (*)

Т1(Стокса-Зайдаля о непрерывности суммы функционального ряда):

Пусть выполняется усл:

1. Все члены u_n(x) ряда (*) явл непрерывными функциями на мн-ве Д

2. Ряд (*) сход равном на мн-ве Д

Тогда сумма S(x) ряда (*) явл непрер функц на мн-ве Д

Т2(о почленном интегриров Функц Ряда)

Пусть выполняется условие

1. Все члены u_n(x) ряда (*) явл непрерывн функциями на мн-ве [a,b]

2. Ряд (*) сход равном на мн-ве [a,b]

Тогда ряд (*) можно интегрировать почленно на любом отрезке [x₀,x] [a,b] и справедл рав-во ==[сх. равн]=

Т3(почленном дифференцировании фукнкц ряда)

Пусть вып усл

1. Ряд (*) сх на [a,b] к функции S(x)

2. Члены ряда (*) – непрер диффер функции на [a,b]

3. Ряд сх-ся равном на [a,b]

Тогда ряд (*) также сх равном на [a,b] и его сумма функц S(x) непрерывно дифференцируема. Причем (x)==

10.1 Степенные ряды. Теорема Абеля. Радиус и интервал (круг) сходимости степенного ряда

Ряд вида либо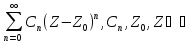называется степенным рядом.

.

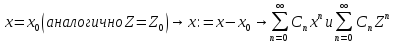Теорема Абеля.

Если степенной ряд сходится при, то он сходится абсолютно для всехтаких, что

Доказательство: Степенной ряд сходится при, т.е. сходится числовой ряд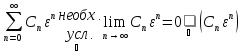ограничена, т.е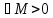, что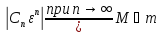

Следствие: Если ряд расходится прито он расходится при всехx таких, что .

10.2 Степенные ряды. Теорема Абеля. Радиус и интервал (круг) сходимости степенного ряда

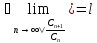Теорема 2. Если либо, где, то радиус сходимости находится по формуле

11.1 Свойства степенных рядов

Теорема 1. Степенной ряд сходится абсолютно и равномерно на.

Доказательство:

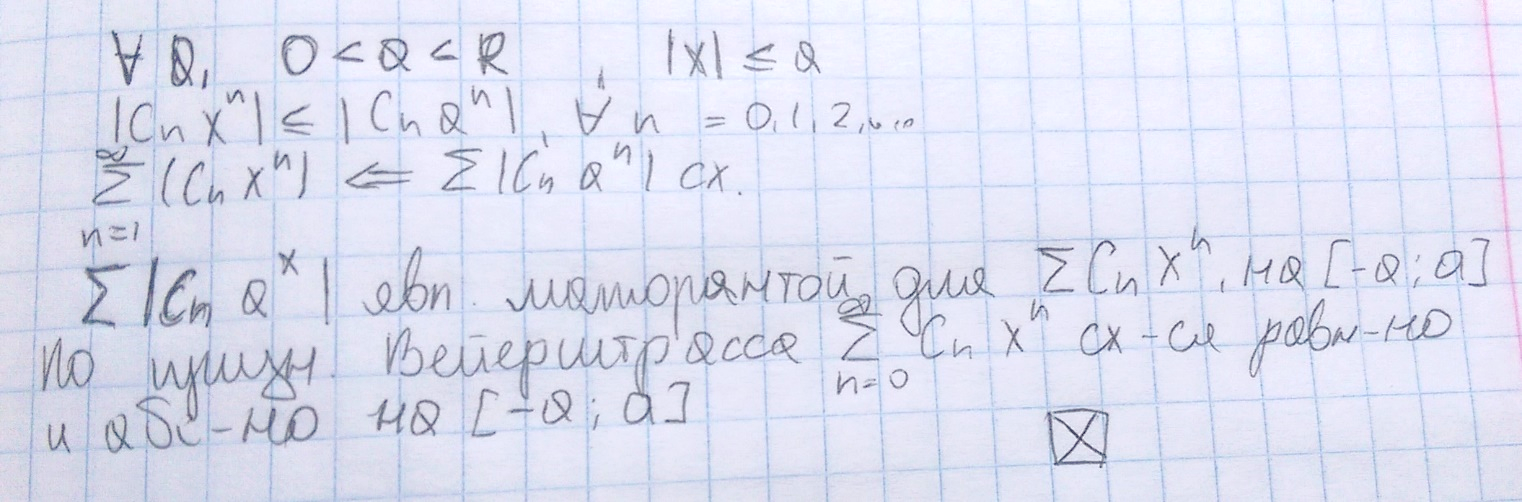
Теорема 2. Сумма степенного ряда

непр. В каждой т.

Доказательство:

Для можем подобрать отрезок

Теорема 3. Если – радиус ходимости степенного ряда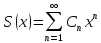, то ряд:

1. можно дифференцировать в интервале сходимости и.

2. Для 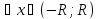ряд можно интегрировать почленно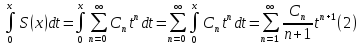

3. Степенные ряды (1) и (2) имеет - ……., при радиусе сходимости –R

12. Ряд Тейлора. Критерий разложимости функции в ряд Тейлора

раскладывается в степенной ряд в интервале, если на этом интервале степенной рядсходится и его сумма равна.

(*)

Теорема. Если функция на интервалераскладывается в степенной ряд(*), то этот ряд раскладывается единственно.

Доказательство:

Рядом Тейлора функции относительноназывается степенной ряд вида

;

При – ряд Маклорена.

Теорема. Для того, чтобы можно было разложить вна интерваленеобходимо и достаточно, чтобы функциябыла бесконечное число раз дифференцируема и.

13. Основные разложения в ряд Маклорена. Приложения степенных рядов

Основные разложения:

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

14. Понятие функции комплексной переменной. Предел и непрерывность

Областью на комплексной плоскости называется открытое сквозное множество D точек комплексной плоскости.

1. Вместе с каждой точкой из D этому множеству принадлежит с дост-ю малый круг с центром в этой точке.

2. Любые 2-е точки из D можно соединить непрерывной кривой мн-ве D – несвязное множество. Эпсилон окрестность точки – открытый круг радиуса эпсилон с центром в точке– окрестность бесконечно удалённой точки.

Область D присоединённой к ней границей называют закрытой областью.

Область расширенной комплексной плоскости называется n-связной, если её граница состоит из n-связных замкнутых множеств, названных компонентами границы.

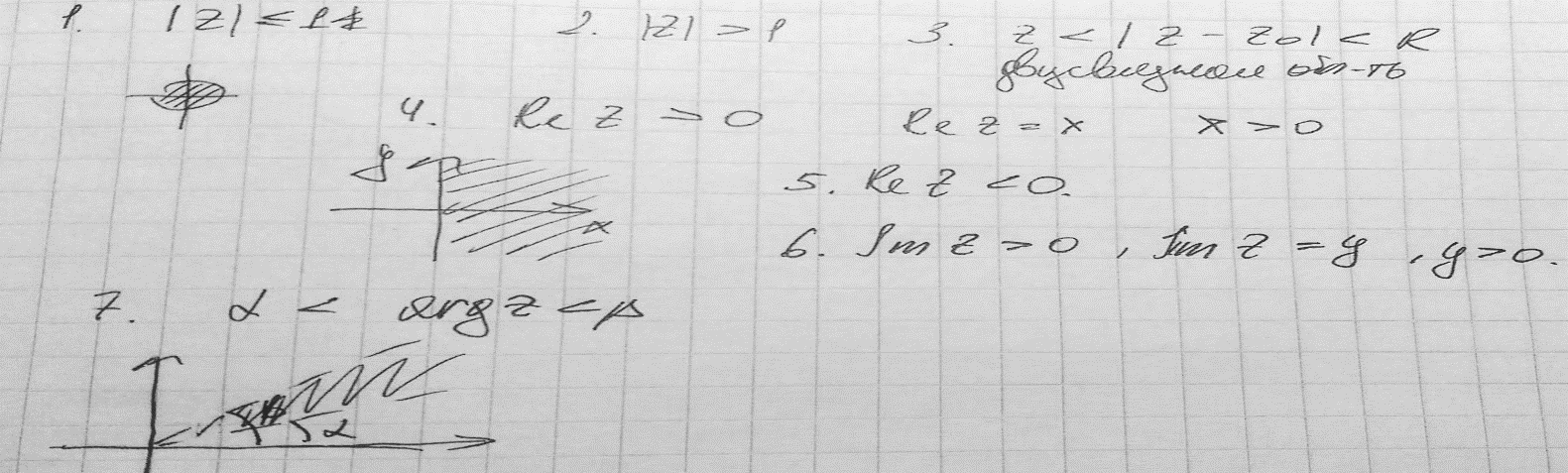
Говорят, что на мно-ве D точек плоскости , если указан закон, по которому в каждой точке функцияявляется однозначной, если каждой точкеz ставится в соответствие только одно значение, в противном случае – многозначной.

определена и однозначна в некоторой окрестности точки

Число называется пределом функциив т., если

функция стремится к пределу не зависимо от способа приближения к точке, т.е если, то припо любому закону(по любой линии, любой последовательности).

Функция заданная наD называется непрерывной в т.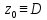, если

, если она непрерывна во всех точках данного множества.