
- •12. Ряд Тейлора. Критерий разложимости функции в ряд Тейлора.
- •1. Числовые ряды. Основные понятия. Действия над рядами. Необходимое условие сходимости ряда
- •2. Интегральный признак сходимости рядов с неотрицательными членами
- •3. Признаки сравнения для рядов с неотрицательными членами
- •4. Признак Даламбера для рядов с неотрицательными членами
- •5. Признак Коши для рядов с неотрицательными членами
- •6. Знакочередующиеся ряды. Признак Лейбница
- •7. Знакопеременные ряды, ряды с комплексными членами. Абсолютная и условная сходимость. Свойства абсолютно и условно сходящихся рядов
- •8. Равномерная сходимость функционального ряда. Признак Вейерштрасса равномерной сходимости
- •9. Свойства равномерно сходящихся функциональных рядов: теоремы о непрерывности суммы, о почленном дифференцировании и почленном интегрировании
- •10.1 Степенные ряды. Теорема Абеля. Радиус и интервал (круг) сходимости степенного ряда
- •15.Основные элементарные функции комплексной переменной
- •16. Производная функции комплексной переменной. Условия Коши-Римана. Аналитические функции. Действительная и мнимая части аналитической функции
- •17. Интеграл от функции комплексной переменной, его вычисление и свойства
- •18. Интегральная теорема Коши. Первообразная и интеграл аналитической функции
- •18. Интегральная теорема Коши. Первообразная и интеграл аналитической функции
- •19.Интегральная формула Коши. Теорема о производных аналитической функции
- •20. Ряды в комплексной области. Свойства функциональных рядов. Степенные ряды
- •21. Ряд Тейлора для функции комплексной переменной. Ряд Лорана
- •22. Нули и изолированные особые точки аналитических функций. Классификация изолированных особых точек
- •23. Понятие вычета. Основная теорема о вычетах
- •24. Вычисление вычетов
- •25. Вычисление интегралов вида,с помощью вычетов
- •26. Скалярное произведение функций. Норма функции. Ортогональные системы функций. Основная тригонометрическая система функций
- •27. Ряды Фурье по ортогональным системам функций
- •28. Сходимость в среднем функционального ряда. Связь между различными видами сходимости. Экстремальное свойство коэффициентов ряда Фурье
- •29. Неравенство Бесселя. Равенство Парсеваля-Стеклова. Полнота и замкнутость ортогональной системы функций
- •30. Тригонометрические ряды Фурье для периодических функций. Признак сходимости тригонометрического ряда Фурье (теорема Дирихле)
- •31. Разложение непериодических функций в тригонометрический ряд Фурье. Ряд Фурье только по косинусам или только по синусам
- •32. Комплексная форма тригонометрического ряда Фурье. Понятие о спектре
- •33. Интеграл Фурье. Комплексная форма интеграла Фурье
- •34. Преобразования Фурье. Косинус- и синус- преобразования Фурье
- •35. Преобразование Лапласа, оригинал и изображение. Основные теоремы операционного исчисления
- •36. Приложение операционного метода к решению дифференциальных уравнений и систем дифференциальных уравнений
1. Числовые ряды. Основные понятия. Действия над рядами. Необходимое условие сходимости ряда.
2. Интегральный признак сходимости рядов с неотрицательными членами.
3. Признаки сравнения для рядов с неотрицательными членами.
4. Признак Даламбера для рядов с неотрицательными членами.
5. Признак Коши для рядов с неотрицательными членами.
6. Знакочередующиеся ряды. Признак Лейбница.
7. Знакопеременные ряды, ряды с комплексными членами. Абсолютная и условная сходимость. Свойства абсолютно и условно сходящихся рядов.
8. Равномерная сходимость функционального ряда. Признак Вейерштрасса равномерной сходимости.
9. Свойства равномерно сходящихся функциональных рядов: теоремы о непрерывности суммы, о почленном дифференцировании и почленном интегрировании.
10.Степенные ряды. Теорема Абеля. Радиус и интервал (круг) сходимости степенного ряда.
11. Свойства степенных рядов.
12. Ряд Тейлора. Критерий разложимости функции в ряд Тейлора.
13. Основные разложения в ряд Маклорена. Приложения степенных рядов.
14. Понятие функции комплексной переменной. Предел и непрерывность.
15.Основные элементарные функции комплексной переменной.
16. Производная функции комплексной переменной. Условия Коши-Римана. Аналитические функции. Действительная и мнимая части аналитической функции.
17. Интеграл от функции комплексной переменной, его вычисление и свойства.
18. Интегральная теорема Коши. Первообразная и интеграл аналитической функции.
19. Интегральная формула Коши. Теорема о производных аналитической функции.
20. Ряды в комплексной области. Свойства функциональных рядов. Степенные ряды.
21. Ряд Тейлора для функции комплексной переменной. Ряд Лорана.
22. Нули и изолированные особые точки аналитических функций. Классификация изолированных особых точек.
23. Понятие вычета. Основная теорема о вычетах.24. Вычисление вычетов.
25.
Вычисление интегралов вида  ,
,


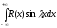 с помощью вычетов.
с помощью вычетов.
26. Скалярное произведение функций. Норма функции. Ортогональные системы функций. Основная тригонометрическая система функций.
27. Ряды Фурье по ортогональным системам функций.
28. Сходимость в среднем функционального ряда, связь между различными видами сходимости. Экстремальное свойство коэффициентов ряда Фурье.
29. Неравенство Бесселя. Равенство Парсеваля-Стеклова. Полнота и замкнутость ортогональной системы функций.
30.Тригонометрические ряды Фурье для периодических функций. Признак сходимости тригонометрического ряда Фурье (теорема Дирихле).
31. Разложение непериодических функций в тригонометрический ряд
Фурье. Ряд Фурье только по косинусам или только по синусам.
32. Комплексная форма тригонометрического ряда Фурье. Понятие о спектре
33. Интеграл Фурье. Комплексная форма интеграла Фурье.
34. Преобразования Фурье. Косинус- и синус- преобразования Фурье.
35. Преобразование Лапласа, оригинал и изображение. Основные теоремы операционного исчисления.36. Приложение операционного метода к решению дифференциальных уравнений и систем дифференциальных уравнений.
1. Числовые ряды. Основные понятия. Действия над рядами. Необходимое условие сходимости ряда
Пусть
дана
посл-ть
(аn)
= (a1,a2,a3,…,an),
an
∈
C
Выражение
вида
a1+a2+a3+…+an+…=
 n наз.
числовым
рядом.
a1,a2,…,an
– члены ряда; an
– n-ый
член ряда.
n наз.
числовым
рядом.
a1,a2,…,an
– члены ряда; an
– n-ый
член ряда.
О: Сумма конечного
числа N
первых членов ряда
 n
Sn=
a1+a2+a3+…+an+…=
n
Sn=
a1+a2+a3+…+an+…= n
наз.
n-ой
частичной
суммой
ряда
n
наз.
n-ой
частичной
суммой
ряда
 n
S1=a1;
S2=a1+a2;
Sn=a1+a2+…+an
и
т.
д.
n
S1=a1;
S2=a1+a2;
Sn=a1+a2+…+an
и
т.
д.
О: Если для
последовательности (Sn)
частичных сумм ряда
 n
∃
конечный предел
n
∃
конечный предел
 или не∃,
то ряд
или не∃,
то ряд
 n
наз. расходящимся.
n
наз. расходящимся.
Для
V(bn)
a1=b1,
a2=b2-b1,
a3=b3-b2,
a
n=
bn-
bn-1… n
Sn=bn,
n
Sn=bn,
Vn
= 1,2,3,4
an
∈
C, an
=αn+iβn,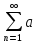 n
=
n
= n
+i
n
+i
 n,
ряд
аn
сход.
cxод. ряд
αn
и ряд βn.
n,
ряд
аn
сход.
cxод. ряд
αn
и ряд βn.
Пр:1)1-1+1-1+1-1+1+(-1)n+1+…
S2k =0, S2k-1=1, k =1,2 1,0,1,0,1,0,1,0,… ряд расход, т к не ∃ конечный предел.
2)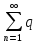 n=q1+q2+q3+..+qn
Sn=
n=q1+q2+q3+..+qn
Sn=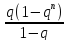
 ,
если |q|<1
,
если |q|<1
 ,
если |q|<1
,
если |q|<1
 ,
если |q|>1
,
если |q|>1
 сход если
|q|<1,
расх, если |q|>1
сход если
|q|<1,
расх, если |q|>1
 ,
еслиq=1
,
еслиq=1
Пусть есть ряд a1+a2+a3+…+an+… (1) и ряд, полученный из него- ã 1+ ã 2+ ã 3+…+ ã n+…(2)
Если ряд 1 сход, тогда и ряд, полученный изменением, либо отображением любого конечного числа членов ряда 1. Вывод: В ряде можно отбросить любое конечное число слагаемых, и это не повлияет на сходимость. Исследование числовых рядов можно начинать с любого места. Пусть ряд 1 сход.
S= n=
n= k
-
k
- k+
k+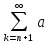 k=Sn+rn
Жирным
выделенn-ый
остаток ряда
k=Sn+rn
Жирным
выделенn-ый
остаток ряда
Т.к. ряд 1 сход, то
 .S=Sn+rn
.S=Sn+rn
 ;
;
 n сх.
n сх.
 Пусть
ряды
Пусть
ряды
 и
и
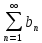 сход. ʎ-некот. Числ. (ʎ∈R
или ʎ ∈С)
тогда сход. И
сход. ʎ-некот. Числ. (ʎ∈R
или ʎ ∈С)
тогда сход. И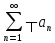 и
и )
)
1)
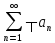 =
=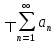 2)
2) )=
)= ±
±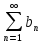 Необх.
Усл. Сх. Ряда: теор: Если ряд
Необх.
Усл. Сх. Ряда: теор: Если ряд сх.(an∈С),то
сх.(an∈С),то
 ;
; сх =>an
сх =>an 0.
Замеч: Необх. Усл. Не явл. Достат! ПР:
0.
Замеч: Необх. Усл. Не явл. Достат! ПР:
 =1+
=1+ +
+ +
+ ряд расх.an=
ряд расх.an= 0
, но Следств: НЕ(an
0
, но Следств: НЕ(an 0),
то ряд расх.
0),
то ряд расх.
