Потехин / Домашняя №1(правка)
.doc
Министерство образования Российской Федерации
ТОМСКИЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ
(ТУСУР)
Кафедра телевидения и управления
(ТУ)
CЛОЖЕНИЕ ЧИСЕЛ СО ЗНАКАМИ В ПРЯМЫХ, ОБРАТНЫХ И ДОПОЛНИТЕЛЬНЫХ КОДАХ
Руководство к проведению практических занятий
Выполнил: студент гр. 165-1
______________Трубинова Н.В.
_________________
Проверил: преподаватель каф. ТУ
______________Потехин В.А.
_________________
Томск
2007
Дано: 186 и 171, числа в десятичной системе счисления.
Задание:
-
перевести данные числа в двоичную, восьмеричную и шестнадцатеричную системы счисления;
-
определить для каждого числа его прямой (
),
обратный (
)
и дополнительный (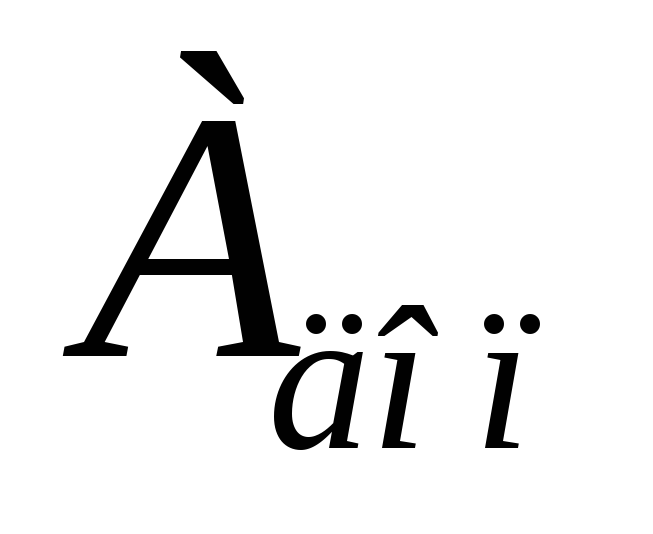
)
коды; -
произвести сложение чисел со знаками в прямых и обратных кодах;
-
произвести сложение чисел со знаками в дополнительных кодах;
-
произвести сложение двоично-десятичных чисел.
Для перевода целых чисел из системы с основанием 10 в систему с основанием 2 необходимо произвести последовательный ряд делений исходного числа на новые основания системы, причем действия производятся в исходной системе счисления. Последовательность остатков, начиная с последнего, дает число в новой системе счисления. Деление производится до тех пор, пока частное не получится меньше основания системы, последнее частное дает старшую степень числа.
- число 186, записанное
в двоичной системе счисления.
|
|
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
|
S
S – знаковый показатель, который ставится в начале двоичного кода;
- число 186, записанное
в восьмеричной системе счисления;
- число 186, записанное
в шестнадцатеричной системе счисления.
Если
,
то закодированное число положительное;
если
,
то закодированное число отрицательное;
если
,
то
- это положительный знак , а
-
входит в полученный результат; если
,
то
- это отрицательный знак , а
- входит
в полученный результат.
При переходе от двоичной системы счисления к восьмеричной (шестнадцатеричной) знаковый показатель не учитывается. Перевод из двоичной системы счисления в восьмеричную (шестнадцатеричную) осуществляется разбиванием двоичного кода на триады (тетрады), начиная с конца, и согласно кодировке записываем число в восьмеричной (шестнадцатеричной) системеуцатеричную восьмеричнуютему счисленияичную (численияньше основаниясчисления.ия.ледовательный ряд делений исходного числ счисления.
|
|
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
|
S
- формула, для
вычисления дополнительного кода числа.
При сложении двух кодов необходимо учитывать:
- в этом случае
пишем в результат сложения, а
переносим в следующий столбец.
- в этом случае
пишем в результат сложения и
переносим в следующий столбец.
|
|
|
S |
S |
|
|
|
|
|
|
• |
|
|
+ |
|
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
|
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
|
|
|
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
|
S
Сделаем проверку:
|
|
|
S |
S |
|
|
|
|
|
|
|
|
|
+ |
|
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
|
|
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
|
|
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
Сумма прямого и обратного кода одного числа равна 1.
Произведем те же операции при обработке числа 171:
- число 171, записанное
в двоичной системе счисления.
|
|
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
|
S
- число 171, записанное
в восьмеричной системе счисления;
- число 171, записанное
в шестнадцатеричной системе счисления.
|
|
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
|
S
|
|
|
S |
S |
|
|
|
|
|
|
|
|
|
+ |
|
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
|
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
|
|
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
S
Сделаем проверку:
|
|
|
S |
S |
|
|
|
|
|
|
|
|
|
+ |
|
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
|
|
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
|
|
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
Сумма прямого и обратного кода одного числа равна 1.
Произведем
сложение прямых и обратных кодов заданных
чисел. Возможны 4 комбинации:
,
,
и
.
|
|
|
|
• |
|
• |
• |
• |
|
• |
|
|
|
+ |
|
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
|
|
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
|
|
|
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
|
Таким образом
|
|
|
• |
• |
• |
• |
• |
• |
|
|
|
|
|
|
+ |
|
|
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
|
|
|
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
|
|
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
|
Имеем:
,
таким образом мы получили код с «лишней»
цифрой в начале. Чтобы избавиться от
нее, произведем циклический перенос,
т.е. прибавим ее к коду
:
|
|
S |
S |
|
|
|
|
|
|
|
|
|
+ |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
Следовательно
|
|
|
|
|
|
|
|
• |
• |
• |
• |
|
|
+ |
|
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
|
|
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
|
|
|
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
|
Получили
.
Обратный код необходимо перевести в
прямой:
|
|
|
• |
• |
|
• |
|
|
|
• |
|
|
|
|
+ |
|
|
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
|
|
|
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
|
|
|
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
|
Произведем
циклический перенос, т.е. к коду
прибавим 1, стоящую в начале полученной
суммы (
).
|
|
|
|
|
|
|
|
|
|
• |
|
|
+ |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
|
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
Таким образом,
получили:
.
Переведем в прямой код:
.