Потехин / next !!! с восьм и шестн
.docxМинистерство науки и образования Российской Федерации
ТОМСКИЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ
(ТУСУР)
Кафедра телевидения и управления
(ТУ)
CЛОЖЕНИЕ ЧИСЕЛ СО ЗНАКАМИ В ПРЯМЫХ, ОБРАТНЫХ И ДОПОЛНИТЕЛЬНЫХ КОДАХ
Выполнил: студент гр. 169
______________Волков Р.С.
_________________
Проверил: преподаватель каф. ТУ
______________Потехин В.А.
_________________
Томск
2011
Дано: A=8285 и B=9321, 5222 и 4523, числа в десятичной системе счисления.
Задание:
-
перевести данные числа в двоичную систему счисления;
-
определить для каждого числа его прямой, обратный и дополнительный коды;
-
произвести сложение чисел со знаками в прямых и обратных кодах;
-
произвести сложение чисел со знаками в дополнительных кодах;
-
произвести сложение двоично-десятичных чисел.
Для перевода целых чисел из системы с основанием 10 в систему с основанием 2 необходимо произвести последовательный ряд делений исходного числа на новые основания системы, причем действия производятся в исходной системе счисления. Последовательность остатков, начиная с последнего, дает число в новой системе счисления. Деление производится до тех пор, пока частное не получится меньше основания системы, последнее частное дает старшую степень числа.
A=8285D = 1·213 + 1·26 +1·24 + 1·23 + 1·22 + 1·20 = 10000001011101B
10000001011101B - число 8285, записанное в двоичной системе счисления.
|
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
|
Aпр.
=
S
Aпр. = 20135O = 205DH
S – знаковый показатель, который ставится в начале двоичного кода;
20135O - число 8285, записанное в восьмеричной системе счисления;
205DH - число 8285, записанное в шестнадцатеричной системе счисления.
Если
,
то закодированное число положительное;
если
,
то закодированное число отрицательное;
если
,
то
- это положительный знак , а
-
входит в полученный результат; если
,
то
- это отрицательный знак , а
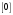- входит
в полученный результат.
При переходе от двоичной системы счисления к восьмеричной (шестнадцатеричной) знаковый показатель не учитывается. Перевод из двоичной системы счисления в восьмеричную (шестнадцатеричную) осуществляется разбиванием двоичного кода на триады (тетрады), начиная с конца, и согласно кодировке записываем число в восьмеричной (шестнадцатеричной) системеуцатеричную восьмеричнуютему счисленияичную (численияньше основаниясчисления.ия.ледовательный ряд делений исходного числ счисления.
|
|
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
|
Aобр.=
S
Aобр. = 157642O = DFA2H
Aдоп. = Aобр. + 1 - формула, для вычисления дополнительного кода числа.
При сложении двух кодов необходимо учитывать:
- в этом случае
пишем в результат сложения, а
переносим в следующий столбец.
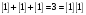- в этом случае
пишем в результат сложения и
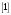переносим в следующий столбец.
|
|
|
S |
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
Aобр. = |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
Aдоп.=Aобр.+ 1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
|
|
Aдоп. = |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
|
S
Aдоп. = 150643O= D1A3H
Сделаем проверку:
|
|
|
S |
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
Aпр. = |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
|
Aобр. = |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
|
|
S=Aпр.+Aобр.= |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
Сумма прямого и обратного кода одного числа равна 1.
Произведем те же операции при обработке числа B=9321:
B=9321D = 1·213 + 1·210 +1·26 + 1·25 + 1·23 + 1·20 = 10010001101001B
10010001101001 - число 9321, записанное в двоичной системе счисления.
|
|
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
|
Bпр.
=
S
22151O - число 9321, записанное в восьмеричной системе счисления;
2469H - число 9321, записанное в шестнадцатеричной системе счисления.
|
|
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
Bобр.=
S
Bобр.= 155626O + DB96H
Bдоп. = Bобр. + 1
|
|
|
S |
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
Bобр. = |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
Bдоп.=Bобр.+ 1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
|
|
Bдоп. = |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
|
S
Bдоп. = 155627O= DB97H
Сделаем проверку:
|
|
|
S |
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
Bпр. = |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
|
Bобр. = |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
|
|
S=Bпр.+Bобр.= |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
Сумма прямого и обратного кода одного числа равна 1.
Произведем сложение первой пары чисел в дополнительных кодах
A = 1558 (обр.) = 11011012 (обр.) = 11011102 (доп.) = 00100102 (пр.) = 1810
В = 7С16 (доп.) = 11111002 (доп.) = 11110112 (обр.) = 00001002 (пр.) = 410
Возможны 4 комбинации: А+В; А-В; -А+В; -А-В.
|
А+В |
|
|
|
|
|
|
|
|
|
|
|
+ |
Апр |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|
Впр |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
|
S=22 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
|
Полученное число 00.0010110
|
А-В |
• |
• |
• |
• |
• |
|
|
|
|
||
|
+ |
Апр |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|
|
Вдоп |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
||
|
S=14 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
|
Получили код с «лишней» цифрой в начале, которая отбрасывается: 00.0001110
|
-А+В |
|
|
|
|
|
• |
• |
|
|
|
|
+ |
Адоп |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
|
Впр |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
|
S= -14 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
|
Обратный код необходимо перевести в прямой: 11.0001101
|
-А-В |
• |
• |
• |
• |
• |
• |
• |
|
|
||
|
+ |
Адоп |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
|
|
Вдоп |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
||
|
S= -22 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
|
Получили код с «лишней» цифрой в начале, которая отбрасывается.
Обратный код необходимо перевести в прямой: 11.0010101
Произведем сложение второй пары чисел в обратных кодах
A = 2078 = 100001112 (пр.) = 011110002 (обр.) = 011110012 (доп.) = 13510
В = С016 = 110000002 (пр.) = 001111112 (обр.) = 010000002 (доп.) = 19210
Возможны 4 комбинации: А+В; А-В; -А+В; -А-В.
|
А+В |
|
|
• |
|
|
|
|
|
|
|
|
|
+ |
Апр |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
|
Впр |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
S=327 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
|
Видно переполнение, но число положительное: 0.101000111