
Министерство образования Российской Федерации
Томский государственный университет
СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра телевидения и управления (ТУ)
Синтез счетчика с параллельным переносом
Контрольная работа №3 по дисциплине "Цифровые устройства и микропроцессоры"
Руководитель:
В.А. Потехин
2003
-
Введение.
В данной контрольной работе будет производиться синтез счетчика с параллельным переносом. Счетчик будет собран на основе JK-триггеров. Максимальный коэффициент пересчета Kmax и пропуск трех текущих значений счетчика К1, К2, К3 будет задаваться комбинационной схемой, обеспечивающей требуемую логику переходов. Для получения заданного Kmax требуется n триггеров, причем 2n > Kmax.
Для данной работы Kmax = 13, К1 = 4, К2 = 6, К8 = 8 (вариант 19, выбранный на основании общего правила). Для синтеза счетчика потребуется 4 JK-триггера.
-
Расчетная часть.
Функциональная схема счетчика представлена на рис. 2.1.
Р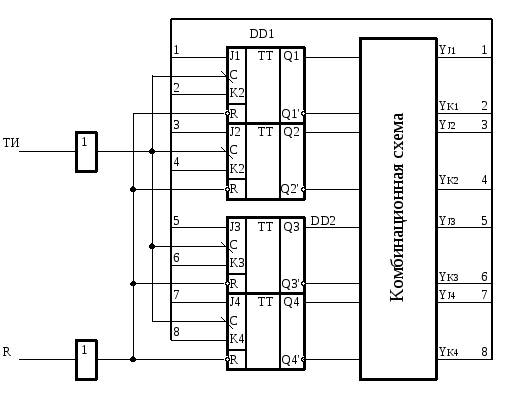 исунок
2.1 - Функциональная схема счетчика.
исунок
2.1 - Функциональная схема счетчика.
Счетные входы всех триггеров и входы установки исходного состояния объединяем. На входах JK-триггеров необходимо установить комбинационные схемы, обеспечивающие требуемую логику переходов.
Закон функционирования JK-триггера иллюстрируется сокращенной таблицей переходов (таблица 2.1). В таблице показаны все возможные переходы триггера из одного состояния в другое, в ней символом Ф обозначено безразличное состояние.
Таблица 2.1.
-
J
K
Qn
Qn+1
0
Ф
0
0
1
Ф
0
1
Ф
1
1
0
Ф
0
1
1
Под действием входных импульсов счетчик переходит из одного состояния в другое. Комбинация состояний выходов триггеров определяет двоичное число на выходе счетчика. Значение этого числа увеличивается на единицу или устанавливается равным нулю после достижения максимального значения N-1. Такие переходы из одного состояния в другое заносятся в таблицу переходов каждого триггера счетчика (таблица 2.2).
Для осуществления таких переходов на входах J и K каждого из триггеров должна быть установлена соответствующая комбинация управляющих сигналов Jn Kn, необходимых для функционирования счетчика по заданному алгоритму.
Задано Kmax = 13, пропустить К1 = 4, К2 = 6, К8 = 8. Заполним таблицу переходов триггеров Т1-Т4 и управляющих сигналов Ji и Ki на их входах, обеспечивающих эти переходы. Для заполнения n-ой строки для выходов триггеров Q1-Q4 в предыдущую n-1 строку для входов J и K вписываются те значения, которые обеспечивают переход триггеров из исходного состояния (строка n-1) в новое состояние (строку n). В результате описания всех переходов получаем таблицу функционирования синтезируемого счетчика (таблица 2.2).
Таблица 2.2 - Таблица переходов триггеров.
-
N
Q4
Q3
Q2
Q1
J4
K4
J3
K3
J2
K2
J1
K1
0
0
0
0
0
0
Ф
0
Ф
0
Ф
1
Ф
1
0
0
0
1
0
Ф
0
Ф
1
Ф
Ф
1
2
0
0
1
0
0
Ф
0
Ф
Ф
0
1
Ф
3
0
0
1
1
0
Ф
1
Ф
Ф
1
Ф
0
5
0
1
0
1
0
Ф
Ф
0
1
Ф
Ф
0
7
0
1
1
1
1
Ф
Ф
1
Ф
1
Ф
0
9
1
0
0
1
Ф
0
0
Ф
1
Ф
Ф
1
10
1
0
1
0
Ф
0
0
Ф
Ф
0
1
Ф
11
1
0
1
1
Ф
0
1
Ф
Ф
1
Ф
1
12
1
1
0
0
Ф
0
Ф
0
0
Ф
1
Ф
13
1
1
0
1
Ф
1
Ф
1
0
Ф
Ф
1
Минимизацию логических функций проведем с помощью карт Карно. Карты Карно для восьми переменных J4 K4…J1 K1 выглядят так, как это показано на рис. 2.2.
|
|
|
|
|
Q2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q3 . |
Q4 . |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
|
|
|
1 |
|
1 |
1 |
|
|
0 |
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
0 |
1 |
0 |
|
|
1 |
|
|
|
|
|
|
1 |
||
|
|
|
J4 |
|
J3 |
|
J2 |
|
J1 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
|
|
1 |
0 |
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
|
|
|
1 |
|
|
|
0 |
0 |
|
|
|
|
0 |
1 |
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
0 |
0 |
0 |
|
|
|
|
|
|
|
|
1 |
0 |
|
|
1 |
1 |
|
|
|
|
K4 |
|
K3 |
|
K2 |
|
K1 |
||||||||||||
Рисунок 2.2 - Карты Карно.
По картам Карно запишем минимизированные выражения для функций J4 K4…J1 K1.
J1 = 1 K1 = Q4 + Q?2'·Q3'·Q4'*
*J2 = Q1·Q?4' + Q3'·Q4 K2 = Q1
J3 = Q1·Q2 K3 = Q2 + Q1·Q4
J4 = Q2·Q3 K4 = Q1·Q3
Соотношения для J2, K1, K3 преобразуем по правилу де Моргана:
J2 = Q1·Q4' + Q3'·Q4 = ((Q1·Q4')'·(Q3'·Q4)')'
K1 = Q2'·Q3'·Q4' + Q4 = ((Q2'·Q3'·Q4')'·Q4')' = ((Q2 + Q3 + Q4)·Q4')' = ((Q2 + Q3)·Q4')' =
= ((Q2'·Q3')'·Q4')'
K3 = Q2 + Q1·Q4 = (Q2'·(Q1·Q4)')'
Для реализации выберем серию К555, из которой берем сдвоенный JK-триггер К555ТВ6 и логические схемы К555ЛА3 и К555ЛИ1. Полный переход к логике И-НЕ намного усложнит комбинационную схему. Для построения комбинационной схемы управления счетчиком (рис. 2.1) требуется два корпуса микросхем триггеров, два корпуса логической схемы 4х2И-НЕ и один корпус логической схемы 4х2И. Логическая ячейка DD1.1 используется в цепи управления по тактовому входу С.
Синтезированная схема спроектированного счетчика представлена в приложении 1.
