
- •Раздел 2. Алгебра множеств Тема 2.1 Основные определения теории множеств. Примеры.
- •Тема 2.2 Подмножество. Понятие универсального множества. Подмножество
- •Универсальное множество
- •Тема 2.3 Операции над множествами.
- •Пересечение множеств.
- •2. Объединение множеств
- •3. Разность множеств
- •4. Дополнение множества
- •Тема 2.4 Законы и тождества алгебры множеств
- •Тема 2.5. Понятие кортежа. Декартово произведение множеств
- •Тема 2.6 Понятия соответствия, отображения, отношения, функции.
- •Тема 2.7 Типы отношений.
- •Отношение эквивалентности:
- •Отношение строгого порядка:
- •Отношение нестрогого порядка:
- •Тема 2.8 Верхняя и нижняя границы множества. Разбиение множества на классы эквивалентности
Тема 2.2 Подмножество. Понятие универсального множества. Подмножество
Определение: Множество Х является подмножеством Y, если любой элемент множества Х принадлежит множеству Y. Это еще называется нестрогим включением.
Некоторые свойства подмножества:
ХХ - рефлективность
X Y & YZ X Z - транзитивность
X т.е. пустое множество является подмножеством любого множества.
Например:
Пусть Х – множество студентов некоторой группы, Е – множество отличников этой же группы.
EX т.к. группа может состоять только из отличников.
Когда хотят подчеркнуть, что в множестве У есть обязательно элементы, отличные от элементов множества Х, то пишут ХУ. Это называется строгим включением.
Например:
Пусть Х – множество всех курсантов ДВИММУ, Е – множество курсантов электромеханического факультета.
EX т.к. в множестве всех курсантов ДВИММУ, обязательно есть элементы E.
Упражнение: Самостоятельно определить свойства строгого включения.
Универсальное множество
Определение: Универсальное множество – это такое множество, которое состоит из всех элементов, а так же подмножеств множества объектов исследуемой области, т.е.
Если М I , то М I
Если М I , то Ώ(М) I , где под Ώ(М) – понимаются все возможные подмножества М, или Булеан М.
Универсальное множество обычно обозначается I.
Универсальное множество может выбираться самостоятельно, в зависимости от рассматриваемого множества, и решаемых задач.
Например:
Рассматривая множество студентов вашей группы, в качестве универсального множества можно взять и множество студентов ДВГМА, и множество всех людей земли, и множество всех живых существ земли.
Рассматривая множество целых положительных чисел, в качестве универсального множества можно взять и множество целых чисел, и множество действительных чисел, и множество комплексных чисел, и само множество целых положительных чисел.
Более подробно о свойствах универсального множества мы поговорим, обсуждая операции над множествами. Скажем только, что если роль нуля в алгебре множеств играет пустое множество. То универсальное множество, играет роль единицы в алгебре множеств.
Тема 2.3 Операции над множествами.
Теперь определим операции над множествами.
Пересечение множеств.
Определение: Пересечением множеств Х и У называется множество, состоящее из всех тех, и только тех элементов, которые принадлежат и множеству Х и множеству У.
Например: Х={1,2,3,4} У={2,4,6} пересечением {2,4}

Определение: Множества называются непересекающимися, если не имеют общих элементов, т.е. их пересечение равно пустому множеству.
Например: непересекающимися множествами являются множества отличников группы и неуспевающих.
Данную операцию можно распространить и на большее чем два число множеств. В этом случае это будет множество элементов, принадлежащих одновременно всем множествам.
Свойства пересечения:
X∩Y = Y∩X - коммутативности
(X∩Y) ∩Z =X∩ (Y∩Z)=X∩Y∩Z - ассоциативности
X∩ =
X∩I = Х
2. Объединение множеств
Определение: Объединением двух множеств называется множество, состоящее из всех и только тех элементов, которые принадлежат хотя бы одному из множеств Х или У.
Например: Х={1,2,3,4} У={2,4,6} объединением {1,2,3,4,6}
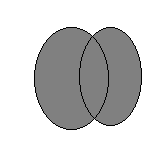
Данную операцию можно распространить и на большее чем два число множеств. В этом случае это будет множество элементов, принадлежащих хотя бы одному из этих множеств.
Свойства объединения:
XUY= YUY- коммутативности
(X UY)UZ =XU (YUZ)=XUYUZ - ассоциативности
XU = X
XUI = I
Из свойств операций пересечения и объединения видно, что пустое множество аналогично нулю в алгебре чисел.
