
Дискретная математика / Основные / КР с примером
.pdf
Контрольные Задания для ИТЗ по дисциплине «математическая логика»
Содержание. |
|
Содержание. .............................. |
1 |
Задание 1. ............................... |
1 |
Задание 2. ............................... |
1 |
Задание 3. ............................... |
1 |
Задание 4. ............................... |
2 |
Задание 5. ............................... |
2 |
Задание 6. ............................... |
2 |
Решение типовых задач .................... |
3 |
ЛИТЕРАТУРА. .............................. |
8 |
Задание 1.
Составить таблицы истинности формул.
1) x y ~( y ↓ x), (x | y) →(z xy).
3) x y ~( y ↓ x), ((x | y) → z) xy.
5) x y →( y x), ((x ~ y) | z) ↓ xy.
7) x y ↓( y → x), ((x | y) ~ z) xy.
9) x ~( y →( y ↓ x)), ((x | y) x z) y.
Задание 2.
2) |
(x ~ |
|
|
) ( y ↓ x), ((x → |
|
|
) | |
|
|
|
) |
|
|
|
. |
||||||||||||||||||
y |
y |
z |
xy |
||||||||||||||||||||||||||||||
4) |
|
|
|
~ |
|
|
( y ↓ |
|
), ((x → |
|
|
) |
|
|
) | |
|
|
|
. |
||||||||||||||
|
|
|
y |
x |
y |
z |
|
xy |
|||||||||||||||||||||||||
|
x |
||||||||||||||||||||||||||||||||
6) |
(x |
|
) ~( y | x), ((x ↓ y) ~ |
|
) |
|
. |
||||||||||||||||||||||||||
y |
z |
xy |
|||||||||||||||||||||||||||||||
8) |
( |
|
y) →( y ↓ x), ((x | |
|
) |
|
) ~z. |
||||||||||||||||||||||||||
x |
y |
xy |
|||||||||||||||||||||||||||||||
10) x ↓( y →( y | x)), x ( y z ~ xy).
Проверьте двумя способами, будут ли эквивалентны следующие функции. А) составлением таблиц истинности; Б) приведением к СДНФ или СКНФ с помощью эквивалентных преобразований.
1) x →( y z), (x → y) (x → z). 3) x ( y z), (x y) (x z). 5) x ( y ↔ z), (x y) ↔(x z).
7) x ( y | z), (x y) | (x z).
9) x ( y → z), (x → y) ↔ (x ↓ z).
Задание 3.
2) |
x | ( y → z), (x | y) →(x | z). |
|
4) |
x ( y → z), |
(x y) →(x z). |
6) |
x ( y → z), |
(x y) →(x z). |
8)x (y → z), (xy) ↔(x z).
10) x ↓( y ↔ z), (x ↓ y) ↔(x ↓ z).
С помощью эквивалентных преобразований приведите формулу к ДНФ, КНФ, СДНФ, СКНФ. Постройте полином Жегалкина методом неопределенных коэффициентов.
1) (x y) →(z x). 2) (x y) →(z x). 3) (x y) →(z x).

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4) |
(x |
y |
) →(z ↔ |
x |
). 5) |
(x | |
y |
) (z → |
x |
). |
6) |
|
(z → x) ↔( y | x) |
. |
|||||||
7) |
|
|
→ x ↔( |
|
| y). 8) |
(z → x) (x | |
|
). |
9) |
|
((x ↓ y) → z) y. |
||||||||||
|
z |
x |
y |
|
|||||||||||||||||
10) ((x | y) → z) y.
Задание 4.
С помощью Карт Карио, построить МДНФ и МКНФ функций: а) f(x,y,z); и в) f(x1,x2,x3,x4) заданных вектором своих значений.
1)a) (1101 0011); б) (1101 1101 0011 0011).
2)а) (1110 0101); б) (1111 1100 1011 1011).
3)а) (1011 1100); б) (1101 0011 1101 0011).
4)а) (1100 0101); б) (1110 0101 0011 0101).
5)а) (0111 1100); б) (1100 1011 1111 1011).
6)а) (0101 0011); б) (0101 0101 1110 0011).
7)а) (0111 1010); б) (0011 0011 1101 1101).
8)а) (1101 1001); б) (1011 1011 1100 1111).
9)а) (0011 1100); б) (0101 0011 0101 1110).
10)а) (1110 0011); б) (0011 1101 0011 1100).
Задание 5.
Используя критерий полноты (теорему Поста) проверить, является ли полной система функций S={f1,f2}.
1) f 1 = x y; f 2 = x y.
3)f 1 = x ↔ y; f 2 = x | y.
5) |
f 1 = |
x → |
|
y; |
f 2 = x |
|
. |
|||
y |
||||||||||
7) |
f 1 = x |
|
; f 2 = |
|
y. |
|||||
y |
x |
|||||||||
9)f 1 = x ↔ y; f 2 = x | y.
Задание 6.
2) |
f 1 = x → y; |
f 2 = |
x |
|
y |
. |
||||||||||
4) |
f 1 = x y; |
f 2 = |
|
y. |
||||||||||||
x |
||||||||||||||||
6) |
f 1 = |
|
|
|
y; |
f 2 = x | |
|
|
|
|||||||
x ↔ |
y. |
|||||||||||||||
8) |
f 1 = x → |
|
|
; |
f 2 = |
|
y. |
|||||||||
y |
x |
|||||||||||||||
10) |
f 1 = |
|
|
|
; |
f 2 = x |
|
. |
||||||||
x |
y |
y |
||||||||||||||
Используя теорему о дедукции и теорему о полноте проверить выводимость формулы ИВ.
1) A |
|
, |
|
|
→ |
|
├ A → |
|
|
2) |
|
A → B, B →C ├B →(A →C). |
||||||||||||
B |
A |
B |
B. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
3) A → B ├ B →(A →C) |
4) |
|
A |
|
, ├ A |
|
|
|||||||||||||||||
A |
A |
|||||||||||||||||||||||
5) (A → B) → B, |
|
├ A |
6) |
(A → B), B ├ A C → B C |
||||||||||||||||||||
B |
||||||||||||||||||||||||
7) (A → B), C ├(A C) →(B C) |
8) |
|
|
→ B A, |
├ A → B |
|||||||||||||||||||
|
A |
|||||||||||||||||||||||
9) A → B , |
|
├B |
10) |
|
A B → |
|
, |
A ├ A B |
||||||||||||||||
A |
|
B |
||||||||||||||||||||||

Решение типовых задач
Пример 1. Составить таблицы истинности формул.
А) x ↔ y →( y x).
Используя введенное старшинство связок, получаем, что данная формула равносильна x ↔( y →( y x)).
Составляем таблицу истинности
x |
y |
|
|
|
Y X |
|
|
→(Y X ) |
x ↔( |
|
→( y x)) |
|
|
Y |
y |
||||||||
Y |
|||||||||||
|
|
|
|
|
|
|
|
||||
0 |
0 |
1 |
|
0 |
|
0 |
1 |
||||
0 |
1 |
0 |
|
1 |
|
1 |
0 |
||||
1 |
0 |
1 |
|
1 |
|
1 |
1 |
||||
1 |
1 |
0 |
|
0 |
|
1 |
1 |
||||
Б) |
|
|
F = x | (( |
y |
|
z |
) ↓ |
xz |
). |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Составляем таблицу истинности |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
X |
|
Y |
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X·Z |
|
|
|
( |
|
|
|
) ↓( |
|
). |
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
z |
xz |
||||||||||||||||
|
Y |
|
|
|
Z |
|
|
Y |
Z |
|
XZ |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
0 |
0 |
0 |
|
1 |
|
|
1 |
|
1 |
|
|
|
0 |
|
1 |
|
0 |
|
|
1 |
||||||||||||
0 |
0 |
1 |
|
1 |
|
|
0 |
|
1 |
|
|
|
0 |
|
1 |
|
0 |
|
|
1 |
||||||||||||
0 |
1 |
0 |
|
0 |
|
|
1 |
|
1 |
|
|
|
0 |
|
1 |
|
0 |
|
|
1 |
||||||||||||
0 |
1 |
1 |
|
0 |
|
|
0 |
|
0 |
|
|
|
0 |
|
1 |
|
0 |
|
|
1 |
||||||||||||
1 |
0 |
0 |
|
1 |
|
|
1 |
|
1 |
|
|
|
0 |
|
1 |
|
0 |
|
|
1 |
||||||||||||
1 |
0 |
1 |
|
1 |
|
|
0 |
|
1 |
|
|
|
1 |
|
0 |
|
0 |
|
|
1 |
||||||||||||
1 |
1 |
0 |
|
0 |
|
|
1 |
|
1 |
|
|
|
0 |
|
1 |
|
0 |
|
|
1 |
||||||||||||
1 |
1 |
1 |
|
0 |
|
|
0 |
|
0 |
|
|
|
1 |
|
0 |
|
1 |
|
|
0 |
||||||||||||
Пример 2. Проверьте двумя способами, будут ли эквивалентны следующие функции. А)составлением таблиц истинности; Б)приведением к СДНФ или СКНФ с помощью эквивалентных преобразований.
Решение. А) Составляем таблицы истинности для функций
F1 = x | ( y z) ; F2 =(x | y) (x z).
|
X Y Z |
Y Z |
F1 |
X|Y |
X|Z |
F2 |
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
Видно, что F1 и F2 не эквивалентны, т.к. например, на наборе (0,0,0)
функция F1 =1, а функция F2 =0, т.е. F1 (0,0,0)≠ F2 (0,0,0).

Б)
F1 = x | ( y z) = x ( y z) = x ( y z) = x ( yz yz) = x yz yz =
= x ( y z) ( y z) = x ( y z) ( y z) =(x y z) (x y z) –СКНФ.
F2 =(x | y) (x | z) =(x y) (x z) = x y (x z) (x y) (x z) =
=xy (x z) (x y) xz =xyz xyz =x(yz yz) =(x yy) (yz y) (yz z) =
=(x y zz)(x y zz)(y z xx)(z y xx) =(x y z)(x y z)(x y z)
(x y z)(y z x)(y z x)(z y x)(z y x) =(x y z)(x y z)(x y z)
(x y z) (y z x)(z y x).
Функция F1 не эквивалентна F2 т.к. СКНФ у них различные (даже по количеству членов).
Пример 3. С помощью эквивалентных преобразований приведите формулу к ДНФ, КНФ, СДНФ, СКНФ. Постройте полином Жегалкина методом неопределенных коэффициентов.
F =((x ↓ y) → z) ↔ y
Решение:
Приведем функцию к базису S1 ={┐,&,v}
F =(x y →) ↔ y =(x y z) ↔ y =(x y z) ↔ y =(x y z y)(x y z y) = = x y z y = x y z y =(x y z) y − КНФ.
Для приведения к ДНФ, применим первый закон дистрибутивности.
F = x y y y z y = x y z y = x y z y –ДНФ
Приведем функцию к СДНФ:
F = x y z y = x y(z z) z y(x x) = x yz x yz z yx z yx = x yz x yz x yz.
Приведем Функцию к СКНФ:
F =(x y z) y =(x y z)( y xx) =(x y z)( y x)( y x) =(x y z)( y x zz) ( y x zz) =(x y z)( y x z)( y x z)( y x z)( y x z).
Для построения полинома Жегалкина, построим таблицу истинности, используя к примеру СДНФ функции F.
X |
Y |
Z |
F |
|
|
|
|
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
Пусть полином Жегалкина имеет вид:

P(x1 y1 z) =c0 c1 x c2 y c3 z c12 xy c13 xz c23 yz c123 xyz.
P(0,0,0)=C0=1 (т.к. F(0,0,0)=1).
P(0,0,1)=C0 C3=0 (т.к. F(0,0,1)=0) 1 c3 =0 c3 =1. P(0,1,0)=C0 C2=0 1 c2 =0 c2 =1.
P(1,0,0)=C0 C1=1 1 c1 =1 c1 =0.
P(0,1,1)=C0 C2 С3 С23=0 1 1 1 c23 =0 1 c23 =0 c23 =1. P(1,0,1)=C0 C1 С3 С13=1 1 0 1 c13 =1 0 c13 =1 c13 =1. P(1,1,0)=C0 C1 С2 С12=0 1 0 1 c12 =0 c12 =0.
P(1,1,1)=C0 C1 С2 С3 С12 С13 С23 С123=0
1 0 1 1 0 1 1 c123 =0 1 c123 =0 c123 =1.
Итак, получаем полином P(x, y, z) =1 y z xy yz xyz – полином Жегалкина 3-й степени.
Пример 4. С помощью Карт Карно, построить МДНФ и МКНФ функций
а)f(x,y,z) и б)f(x1 ,x2 ,x3 ,x4 ) заданных вектором своих значений.
А) (1011 0101), Б) (1011 1111 1011 1100).
Решение. А) Занесем данные в карту Карно. Удобно сначала отметить клетки, где функция равна нулю. Функция f равна нулю на наборах, являющимся двоичными разложениями чисел 1,4,6 (т.к. отсчет начинается с О). Таким образом, f(0,0,1)=f(1,0,0)=f(1,1,0)=0.
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
1 |
|||||
|
|
x |
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f = xz |
|
|
|
|
|
|
|
||||
xy xz − min Д.Н.Ф. |
|
||||||||||
Для построения МКНФ, построим МДНФ для функции f :
f :
|
y |
|
1 |
1 |
1 |
x
z
f = xz x yz .
Переходя к функции f, получим:
f= f = xz x yz =(x z)(x y z) –МКНФ.
Б) Заносим данные в карту Карно. Рассуждая как в предыдущем случае, получаем, что
f(0,0,0,1)=f(1,0,0,1)=f(1,1,1,0)=f(1,1,1,1)=0.
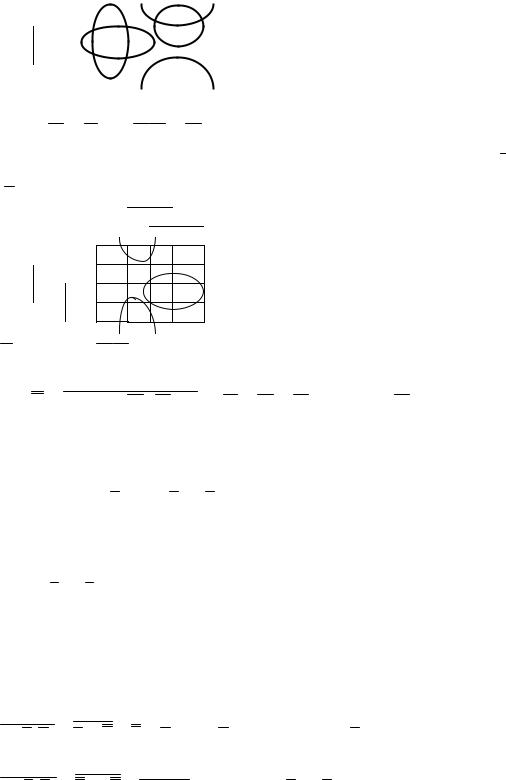
f:
|
|
X4 |
|
|
|
X2 |
|
|
|
X3 |
|
1 |
|
1 |
1 |
||
|
|
1 |
1 |
1 |
1 |
|
X1 |
1 |
1 |
|
|
|
1 |
|
1 |
1 |
|
f = x2 x3 x1 x3 x3 x4 x2 x3 –МДНФ.
Для построения МКНФ Функции f, построим сначала МДНФ, функции, f .
f :
X4
X3
X2 1
1 1
X1 1
f = x1 x2 x3 x2 x3 x4 .
Используя правила де Моргана, получаем:
f = f = x1 x2 x3 x2 x3 x4 =(x1 x2 x3 )(x2 x3 x4 ) –МКНФ.
Пример 5. Используя критерий полноты (теорему Поста) проверить, является ли полной система функций S={f1,f2}.
f1 = x y; f2 = x → y.
Решение: Проверим какими свойствами обладают данные функции. 1. Сохранимость константы О.
f1(0,0)=0*1=0 – сохраняет константу О.
f2(0,0)= 0 →0 =1 →1 =1 – не сохраняет константу 0.
2. Сохранимость константы 1. f1(1,1)=1*0=0 – не сохраняет константу 1. f2(1,1)=0 →0=1 – сохраняет константу 1.
3. Самодвойственность.
f1 (x, y) = x y = x y = x y ≠ f1 (x, y) = x y – не самодвойственна. Составим таблицы истинности для функций:
f2 (x, y) = x → y = x → y, и f2 (x, y) = x → y.
X Y |
X→Y |
|
|
|
|
|
|
|
|
|
|
|
→ |
|
|
|
X →Y |
X |
Y |
|
|||||||||||||
|
|
X |
Y |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
0 |
0 |
1 |
|
0 |
|
1 |
|
1 |
|
1 |
|
|
||||
0 |
1 |
1 |
|
0 |
|
1 |
|
0 |
|
0 |
|
|
||||
1 |
0 |
0 |
|
1 |
|
0 |
|
1 |
|
1 |
|
|
||||
1 |
1 |
1 |
|
0 |
|
0 |
|
0 |
|
1 |
|
|
||||

Из таблицы истинности видно, что f2 (x, y) = x → y ≠ f2 (x, y) = x → y т.е. f2-не самодвойственна.
4. Линейность.
Построим полином Жегалкина для функции f2 методом неопределенных коэффициентов. P(x,y) имеет вид:
P(x, y) =c0 c1 c2 y c3 xy.
Используя таблицу истинности для f2, полученную в п.3, имеем
P(0,0)=C0=1 C0=1
P(0,1)=C0 C2=0 1 C2=0 C2=1
P(1,0)=C0 C1=1 1 C1=1 C1=0
P(1,1)=C0 C1 C2 C3=1 1 0 1 C3=1 C3=1.
Итак, f2=1 y xy – не линейна.
5. Монотонность.
Очевидно, что наборы упорядочены следующим образом: (0,0)≤(0,1); (0,0)≤(1,0); (0,0)≤(1,1); (0,1)≤(1,1); (1,0)≤(1,1).
Проверим на монотонность функцию f1: f1(0,0)=0*1=0 ≤ f1(0,1)=0*0=0;
f1(0,0)=0 ≤ f1(1,0)=1*1=1; f1(0,0)=0 ≤ f1(1,1)=1*0=0; f1(0,1)=0*0=0 ≤ f1(1,1)=1*0=0; f(1,0)=1*1=1 ≥ f1(1,1)=1*0=0.
Итак, мы получили, что для (1,0)≤(1,1), не выполняется f1(1,0)≤f1(1,1), следовательно функция f1–не монотонна.
Проверим на монотонность функцию f2(0,0)=1; f2(0,1)=0. Итак, для (0,0)≤(0,1) мы не получили что f2(0,0)≤ f(0,1). Следовательно f2–не монотонна.
Сведем наши вычисления в таблицу.
Функция |
Не |
Не |
Не |
Не |
Не |
|
сохр.0 |
Сохр.1 |
Самодв. |
Линейность |
Монотонность |
f1 |
|
* |
* |
* |
* |
f2 |
* |
|
* |
* |
* |
Из теоремы Поста, заключаем, что система S ={x y, x → y}– полная.
Задание 6. Используя теорему о дедукции и теорему о полноте проверить выводимость формулы ИВ.
Решение: Используя теорему о дедукции последовательно, заключаем, что
А→В, В→А ├ AB BA А→В ├ (В→А)→( AB BA) ├ (А→В)→((В→А)→
→( AB BA)).
По теореме о полноте заключаем, что формула ϕ=(А→В) ((В→А)→( AB BA)) доказуема тогда и только тогда, когда ϕ является тавтологией. Построим таблицу истинности для формулы ϕ.

A |
B |
A→B |
B→A |
|
|
|
|
|
|
|
|
B |
|
|
A |
|
|
|
(В→А)→( |
|
|
ϕ |
||||
A |
|
|
B |
|
|
A |
B |
AB |
BA |
AB |
BA) |
|||||||||||||||
0 |
0 |
1 |
1 |
|
1 |
|
1 |
|
0 |
|
0 |
|
0 |
|
|
0 |
|
|
|
0 |
||||||
0 |
1 |
1 |
0 |
|
1 |
|
0 |
|
1 |
|
0 |
|
1 |
|
1 |
|
1 |
|||||||||
1 |
0 |
0 |
1 |
|
0 |
|
1 |
|
0 |
|
1 |
|
1 |
|
1 |
|
1 |
|||||||||
1 |
1 |
1 |
1 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|||||||||
Т.к. ϕ не является тавтологией, (т.е. не равна тождественно 1), то следовательно формула AB BA не выводится из формулы А→В и В→А .
ЛИТЕРАТУРА.
1.Ф.А.Новиков. Дискретная математика для программистов./ Санкт-Петербург: Питер, 2001г., 304С.
2.С.В.Судоплатов, Е.В.Овчинникова. Элементы Дискретной математики./ М., ИНФРА-М, Новосибирск, Изд-во НГТУ, 2002г., 208С.
3.В.Н.Нефедов, В.А.Осипова Курс дискретной математики./ М., Изд-во МАИ, 1992г., 264С.
