хашимов / лабы задания / Лабораторная работа 1

Лабораторная работа № 1. ПОЛЯРИЗАЦИЯ ПЛОСКИХ ВОЛН

Цель работы

1.Экспериментальное и теоретическое исследование поляризационных явлений плоских электромагнитных волн.

2.Экспериментальное исследование методов формирования заданных поляризационных характеристик плоских электромагнитных волн.

1. Поляризационные характеристики плоских волн

Под поляризацией плоской волны условно понимают пространственную ориентацию вектора напряженности электрического поля E . Плоскость, проходящую через направление распространения волны и вектор E , называют плоскостью поляризации. Рассмотрим плоскую волну с комплексной векторной

плоскость поляризации проходит через оси x и z , следовательно, волна имеет линейную поляризацию. Поляризационные свойства плоской волны определяются

практических приложениях часто рассматривают плоские волны, которые распространяются в обратном направлении, то есть в направлении отрицательных z . Для этих волн необходимо вместо электрической длины βz записывать −βz в соответствующих выражениях. Рассмотрим свойства волны в некоторой фиксированной точке z , например, z = 0 . Тогда ортогональные компоненты принимают следующий вид:

5

Обозначим через ϕ = ϕa − ϕb . Исключая из соотношений (1.3) переменные cos ωt и sin ωt , получим обобщенное уравнение эллипса:

частных случаях может трансформироваться в линию или в окружность. Годографом вектора E в различные моменты времени для произвольных A, B, ϕ является эллипс с центром в начале координат и повернутый на некоторый угол ψ относительно координатных осей (рис. 1.1). В любой фиксированной плоскости z = const с течением времени вектор E вращается, описывая своим концом эллипс. Частота вращения вектора E равна частоте электромагнитного поля плоской волны,

поворачивается. В пространстве в фиксированные моменты времени конец вектора E описывает винтовую линию, лежащую на поверхности эллиптического цилиндра. Таким образом, в общем случае плоская волна имеет эллиптическую поляризацию.

сдвига ϕ . Если ϕ > 0 , то Ex опережает E y . Если 0 < ϕ < π , то вектор E совершает

вращение по часовой стрелке, если смотреть в направлении распространения электромагнитной волны. Такую волну называют правополяризованной. Если фазовый сдвиг π < ϕ < 2π , то возникает левополяризованная волна. Механизм образования эллиптической поляризации поясняется рис. 1.2, на котором вместо фиксированной точки и движущейся волны использована остановленная волна и движущаяся точка на поверхности эллиптического цилиндра.

6

Пусть ϕa = 0 , ϕb = −π2 , тогда ϕ = π2 , комплексная амплитуда плоской волны

Рис. 1.4. Круговая поляризация

Для фазового сдвига ϕ = π2 конец вектора E вращается против часовой стрелки, если смотреть в направлении отрицательных значений z (напомним, что на рис. 1.4 ось z направлена на нас).

Рис. 1.5. Варианты круговой поляризации

8

Для радиотехнических приложений теории электромагнитных волн принято, что направление вращения вектора E определяется для наблюдателя, смотрящего вслед уходящей волне, поэтому для волны, распространяющейся в направлении положительных значений z (прямая волна), вектор E будет вращаться по часовой стрелке – это волна правой поляризации (рис. 1.5). Для фазового сдвига ϕ = −π2 , то

есть ϕa = 0 , ϕb = π2 , комплексная амплитуда плоской волны E0 = A(ix + i × i y ) – это

волна левой поляризации, вращение вектора E происходит против часовой стрелки для наблюдателя, смотрящего вслед уходящей волне.

При изменении направления распространения волны на противоположное получим четыре случая правой (левой) поляризации для прямой (обратной) волны:

Таким образом, однородная плоская волна с круговой поляризацией может быть представлена следующим образом:

Текст программы MATLAB позволяет визуально определить проекции вектора E на координатные плоскости для правого и левого направления вращения.

Np=53; % общее количество изображаемых векторов i=1:Np; x(i)=0; ymin=0; ymax=2; y(i)=ymin+(ymax-ymin)/(Np-1)*(i-1);

z(i)=0; Ex0=1; Ez0=1; t=2.3; Ex(i)=Ex0*cos(2*pi*y(i)-2*pi*t-pi/2); Ez(i)=Ez0*cos(2*pi*y(i)-2*pi*t); Ey(i)=0; quiver3(x,y,z,Ex,Ey,Ez);

view([50 36]); axis equal; xlabel('x'); ylabel('z'); zlabel('y');

При теоретическом рассмотрении иногда бывает удобно представить волну линейной поляризации в виде суммы двух волн круговой поляризации с противо- положным направлением вращения. Действительно, пусть вектор E линейно поляризованной волны ориентирован вдоль оси x . Тогда

Первое слагаемое описывает волну круговой поляризации правого вращения, а второе – левого (рис. 1.6).

9

Для практических расчетов достаточно предположить, что плоская волна круговой поляризации падает под углом θ = 0 (нормальное падение, более подробно эти задачи рассмотрены в лабораторной работе № 2) на границу раздела воздух – вода S . В этом случае согласно формулам Френеля коэффициент отражения волны

падающей волны. Отраженная волна характеризуется векторами Eо, Hо, По . Из (1.8) следует, что ρ < 0. Так как exp(iπ) = −1, то это означает, что отраженная волна противофазна падающей.

Eо t1 t2

По

t3

t2 t1 Eп

S

Рис. 1.8. Изменение направления вращения отраженной волны

Следовательно, на поверхности S направление вращения вектора Eо изменяется на противоположное, так как направление распространения отраженной волны противоположно направлению распространения падающей волны, как показано на рис. 1.8. Вследствие симметрии капель воды волна, отраженная от дождя, тумана, будет иметь круговую поляризацию, но противоположного вращения, и приниматься антенной не будет. Сигнал, отраженный от цели, также будет иметь поляризацию противоположного вращения, но не круговую, а эллиптическую, так как цель не имеет, как правило, круговой симметрии. Этот сигнал частично будет принят антенной (объяснить самостоятельно). Очевидно, что энергетические характеристики такой радиолокационной станции будут хуже, чем при линейной поляризации. Поэтому на практике обычно используют линейно поляризованные волны, а на круговую поляризацию переходят только при наличии дождя или тумана. Это достигается использованием антенных систем с управляемой поляризацией.

11

E′x (t ) = Ex (t ) × cos y + Ey (t ) ×sin y;

(1.11)

E¢y (t ) = Ey (t ) × cos y - Ex (t ) ×sin y,

тогда в новой системе координат уравнение эллипса принимает вид:

следовательно, для определения направления вращения вектора E остаются справедливыми правила, приведенные на рис. 1.5.

1.3. Описание лабораторной установки

Основные узлы лабораторной установки показаны на рис. 1.9. Колебания СВЧ от генератора 1, работающего в трехсантиметровом диапазоне волн, с помощью гибкого коаксиального кабеля и коаксиально-волноводного перехода 2 подаются на волноводный Т-образный мост 3, делящий мощность пополам. Для компенсации возможных отражений к Т-образному мосту подключается согласованная нагрузка 7. Канал излучателя 6 содержит аттенюатор 4 и фазовращатель 5. Канал излучателя 9 также содержит аттенюатор 8. Излучатели 6 и 9 представляют собой открытые концы прямоугольных волноводов, обладающие направленными свойствами.

8

9

Рис. 1.9. Функциональная схема лабораторной установки

12

Излучаемые ими волны линейно поляризованы, причем ориентация плоскости поляризации излучаемого поля совпадает с ориентацией вектора E волны H10 . Для получения эллиптической поляризации излучатели 6 и 9 ориентированы ортогонально друг к другу, амплитуды и фазы излучаемых ими электромагнитных полей можно регулировать с помощью аттенюаторов и фазовращателя, получая поляризацию от линейной до круговой (рис. 1.10). Приемное устройство состоит из рупорной антенны 10, также имеющей линейную поляризацию, детекторной секции 11 и измерителя отношения напряжений 12 типа В8-6.

Пластины

волноводных

аттенюаторов

Рис. 1.10. Волноводные тракты излучателей

При выполнении работы необходимо учитывать, что при приеме линейно поляризованной волны сигнал на выходе приемной антенны будет пропорционален косинусу угла между плоскостью поляризации приходящей волны и плоскостью поляризации приемной антенны (рис. 1.11).

y

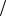ϕ = π2

Рис. 1.11. Поляризационная характеристика поляриметра для линейной поляризации падающей волны

13

Так как электромагнитное поле плоской волны эллиптической поляризации может быть представлено в виде суммы двух независимых линейно поляризован- ных волн с ортогональными плоскостями поляризации, то сигналы на выходе приемной антенны, соответствующие этим волнам, также будут независимы. Таким образом, для фиксированного угла поворота измерительной антенны выходной сигнал может быть представлен в виде суммы двух независимых сигналов. Для квадратичной характеристики детектора график зависимости напряженности измеряемого поля от угла поворота приемной антенны в полярной системе координат будет напоминать по форме гантель (рис. 1.12). В связи с этим такие зависимости в антенной технике называют гантельными кривыми.

1.4.Порядок выполнения работы

1.Изучить руководство к работе.

2.Ознакомиться с лабораторной установкой и приборами, входящими в ее состав. Сдать коллоквиум и получить разрешение на включение приборов.

3.Получить сигнал линейной поляризации, для чего полностью ввести аттенюатор одного из каналов. Аттенюатор другого канала должен быть установлен на минимальное подавление.

4.Ориентировать плоскость поляризации приемной антенны на максимальный сигнал, подстроить детекторную секцию перемещением короткозамыкающего поршня.

14