Пусть необходимо решить систему линейных алгебраических уравнений (слау):

(3.1)

где – неизвестные величины,

–заданные элементы матрицы системы уравнений.

Любую слау можно представить в матричном виде:

, (3.2)

где – матрица коэффициентов (квадратная),

–вектор решения,

–вектор правой части.

Часто используют понятие расширенной матрицы СЛАУ. Эта матрица имеет следующий вид:

(3.3)

или

(3.4)

где .

Методы решения СЛАУ можно подразделить на две группы:

1. Точные. В этом случае заранее известно количество вычислительных операций для получения результата. Ошибка результата в этих методах является результатом накопления ошибок всех операций.

2. Приближённые (итерационные). Количество вычислительных операций заранее неизвестно и зависит от заданной точности.

Рассмотрим некоторые из этих методов.

Точные методы

1. Метод Гаусса

Алгоритм метода состоит из двух этапов. Первый этап называется прямым ходом метода и заключается в последовательном исключении неизвестных из уравнений, начиная с .

Из первого уравнения системы (3.1) выражаем неизвестное :

, (3.5)

что возможно при , в противном случае надо осуществить перестановку уравнений системы. Согласно формуле (3.5) необходимо каждый элемент первой строки расширенной матрицы СЛАУ (3.4) поделить на диагональный элемент

. (3.6)

Затем подставляем выражение (3.5) во все остальные уравнения системы, тем самым исключая из всех уравнений, кроме первого. Элементы расширенной матрицы преобразуем по формуле

(3.7)

В результате исключения первого неизвестного из всех уравнений все элементы первого столбца преобразований матрицы будут равны нулю, кроме.

Неизвестное выразим из второго уравнения системы и исключим из остальных уравнений т.д. В результате получим СЛАУ с верхней треугольной матрицей, у которой все элементы ниже главной диагонали равны нулю.

Запишем выражения для неизвестных и преобразования элементов расширенной матрицы системы, которые обобщают формулы (3.5)–(3.7):

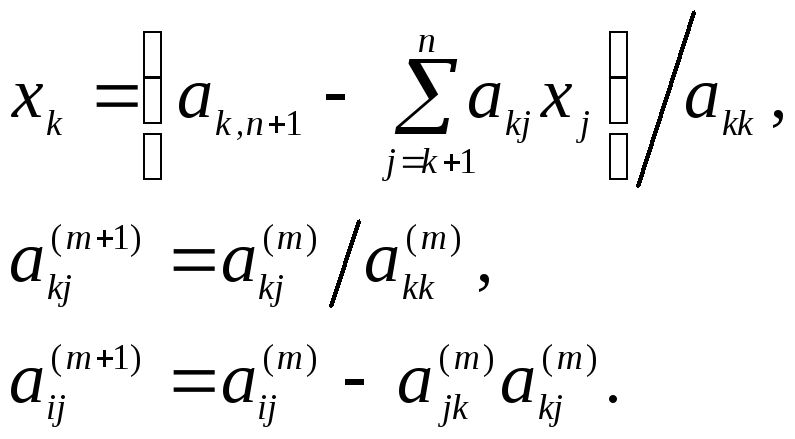(3.8)

Второй этап решения СЛАУ называется обратным ходом метода Гаусса и состоит в последовательном определении неизвестных по первой формуле (3.8), начиная с неизвестногои заканчивая.

Точность результатов будет определяться точностью выполнения арифметических операций при преобразовании элементов матрицы. Для уменьшения погрешности при делении на диагональный элемент (вторая формула (3.8)) рекомендуется осуществить такую перестановку уравнений, чтобы поставить на диагональ наибольший по модулю из всех элементов рассматриваемого столбца. Такая процедура называется выбором главного элемента столбца.

Количество арифметических операций в методе Гаусса связано с размерностью системы и примерно равно . Контроль полученных решений можно провести путём их подстановки в исходную СЛАУ и вычисления невязок, разностей между правыми и левыми частями уравнений:

.

При малой погрешности решений величины будут близки к нулю.

Итерационные методы

2. Метод простых итераций

Для решения СЛАУ итерационными методами преобразуем систему от формы (3.1) к виду

(3.9)

Задав столбец начальных приближений , подставим их в правые части системы (3.9) и вычислим новые приближения, которые опять подставим в систему (3.9), и т.д. Таким образом, организуется итерационный процесс, являющийся обобщение метода простых итераций на системы уравнений:

(3.10)

Можно выделить три достаточных условия сходимости для данного процесса:

а) ,

б) ,

в) .

Выделяют два условия прекращения итерационного процесса:

а) ,

где – метрика пространства.

Понятие метрики пространства. Пусть заданы две точки n-мерного пространства:

и . Тогда метрику этого пространства можно задать тремя способами:

1. ,

2. ,

3. .

б) Чаще используется условие достижения решения с заданной точностью

.

Как и в случае решения СЛАУ методом Гаусса, контроль полученных решений можно произвести путём подстановки их в СЛАУ и вычисления вектора невязок

.

3. Метод Зейделя

Метод Зейделя является модификацией метода простых итераций. При решении СЛАУ методом Зейделя процесс (3.10) видоизменяется, так как используются приближения к решениям, найденные при выполнении текущей итерации. Такое изменение, как правило, приводит к ускорению сходимости. Система (3.10) в таком случае принимает вид

Условия прекращения итерационного процесса для метода Зейделя такие же, как и условия прекращения для метода простых итераций.

4. Источники и виды ошибок при вычислениях

Для получения правильных результатов вычислений необходимо знать:

1. какие бывают ошибки и откуда они берутся,

2. как количественно охарактеризовать ошибку,

3. как грамотно организовать вычисления.

Анализ ошибок в численном результате должен являться непременной составной частью любого серьезного вычисле­ния, независимо от того, производится это вычисление вручную или с помощью ЭЦВМ. Исходная информация очень редко является точной, так как часто исходные величины являются экспериментальными данными или основаны на приблизительных оценках. Кроме того, сами процессы вычислений могут вносить в результат различного рода ошибки.

Например, рассмотрим следующую систему уравнений:

5х-331y = 3.5,

6х-397y = 5.2.

Довольно легко найти «точное» решение этой системы: х = 331.7, у = 5.000, причем решение может быть найдено вручную с любым нужным количеством значащих цифр. Попытаемся оценить количество достоверных знача­щих цифр в этом решении. Проверим сначала, что случится, если константу в правой части второго уравнения изме­нить с 5.2 до 5.1, т. е. приблизительно на 2%. При этом решение системы становится равным х = 298.6, у = 4.5. Этот факт может~вызвать беспокойство: изменение исходной величины на 2% приводит к изменению результата на 10%? Еще более поразительно то, что если подставить в уравнения х = 358.173, у = 5.4, то при округлении вычисленные зна­чения левых частей дадут те же самые правые части, что и в исходной системе уравнений. По-видимому, в этом случае можно считать, что величины х и у имеют не больше одной достоверной значащей цифры.

В данном случае неточность результата не зависит от количества значащих цифр, все вычисления были проделаны точно. Причина неточности в данном случае – малая величина определителя системы уравнений. Геометрически это означает, что две прямые линии, представленные указанными уравнениями, почти параллельны.

Без анализа ошибок вычисления нельзя сказать что-либо определенное относительно точности результата. Иногда, конечно, можно уже при составлении программы быть уверенным, что никаких специфических проблем, связанных с точностью результата, в задаче не встретится. Но вообще говоря, такие случаи являются скорее исключением, чем правилом.

4.1. Виды ошибок

1. Ошибка метода.

Ошибка метода зависит от метода, с помощью которого производится вычисление. В случае с вычислением определённого интеграла, например, ошибка метода получается из-за неточной замены функции на отрезке [].

2. Ошибки ограничения.

Ошибки ограничения связаны с невозможностью увеличить количество итераций либо других операций до бесконечности.

Пример:

.

Представленный пример иллюстрирует нам, как мы заменяем суммирование до бесконечности суммированием до какого-либо достаточно большого числа n.

3. Ошибка округления.

Ошибка округления связана с ограничением разрядной сетки, с помощью которой представляются числа в ЭВМ. Эта ошибка определяется с помощью следующей формулы

,

где – количество значащих цифр в представлении числа. Эта ошибка не превышает половины младшего разряда сетки.

4.2. Относительные и абсолютные ошибки

В процессе численного решения некоторой задачи приходится иметь дело с тремя основными видами ошибок: ошибками, содержащимися в исходной информации, ошибками, возникающими при ограничении бесконечного математического процесса конечным числом операций (ошибки ограничения), и ошибками, возникающими в результате необходимости представлять число в виде конечной после­довательности цифр (ошибки округления). Каждую из этих ошибок можно представить в абсолютной и относительной форме.

Относительные и абсолютные ошибки определяются следующим образом. Абсолютная ошибка есть разность между истинным значением величины (считая это истинное значение известным) и ее приближенным значением. Обычно приближенное значение некоторой величины, или приближение, обозначается тем же символом, что и точное значение, только сверху этого символа ставится черта; ошибка же обозначается буквой е с символом приближаемой величины вместо индекса. Таким образом, если точное значение равно х, то мы должны написать

х = + е_х.

Здесь е_х есть абсолютная ошибка, определяемая как разность между точным значением и приближением:

е_х = x-.

Относительная ошибка определяется, как отношение абсолютной ошибки к приближению. Казалось бы, что более естественно определить ее, как отношение абсолютной ошибки к точному значению, но обычно точное значение нам неизвестно. Все, что обычно бывает известно, это приближенное значение величины и оценка ошибки или границы максимально возможной величины ошибки. Если ошибка мала, то разница в определениях не скажется на численной величине относительной ошибки.

Для величин, близких по значению к единице, абсолютная и относительная ошибки почти одинаковы. Для очень больших или для очень малых величин относительная и абсолютная ошибки представляются совершенно разными числами. Так, если точное значение некоторой величины равно 0.00006, а приближенное значение равно 0.00005, то абсолютная ошибка составляет всего 10^-5, в то время как относительная ошибка составляет 0.2, или 20%. С другой стороны, если точное значение равно 100 500, а приближенное значение равно 100 000, то абсолютная ошибка составляет 500, хотя относительная ошибка составляет всего 0.005, или 0.5%.

Необходимо всегда указывать, какая ошибка имеется ввиду – абсолютная или относительная, если это не ясно из условий задачи или из контекста.

4.3. Ошибки, содержащиеся в исходной информации

Ошибки в исходной информации возникают в результате неточности измерений, грубых просмотров или из-за невозможности представить необходимую величину конечной дробью.

Всякое физическое измерение, будь то измерение расстояния, напряжения или интервала времени, не может быть выполнено абсолютно точно. Если, например, указано, что величина напряжения составляет 6.4837569 в, то можно с уверенностью сказать, что по меньшей мере несколько младших значащих цифр недостоверны, потому что невозможно измерить напряжение с такой точностью. Если же экспериментальный результат содержит небольшое количество значащих цифр (например, промежуток времени в 2.3 сек), то можно быть абсолютно уверенным в том, что эта величина дана с некоторой ошибкой, так как лишь случайно величина интервала времени может составить в точности 2.3 сек. В таких случаях подразумеваются некоторые границы, внутри которых эта величина должна находиться, что-либо вроде 2.3 ± 0.1 сек.

Иногда подразумевается, что если для экспериментального результата не указаны его возможные границы, то результат имеет точность половины единицы младшего разряда. Поэтому если дано, что некая длина равна 5.63 см, то это следует понимать так, что эта длина не меньше 5.625 и не больше 5.635 см. Однако это правило не всегда соблюдается; поэтому, когда границы точности результата важны, их следует указать в явном виде, например 5.63 ± 0.005см.

Независимо от количества значащих цифр в какой-либо величине, в ней может содержаться порой какая-нибудь грубая ошибка. Грубые ошибки могут возникнуть от опечаток, от ошибочного отсчета показаний прибора, хотя встречаются иногда и такие ошибки, возникновение которых связано с некорректной постановкой задачи или с неполным пониманием некоторых физических законов.

Многие числа нельзя представить точно ограниченным числом значащих цифр. Если в вычислениях используется число π, то оно может быть представлено в виде 3.14, или 3.14159265, или 3.141592653589793, в зависимости от того, какая точность требуется в данном вычислении. В любом случае, однако, невозможно представить π точно, так как π является иррациональным числом и не может быть представлено конечным числом знаков. Даже обыкновенные дроби очень часто нельзя представить с помощью конечного числа десятичных знаков, как 1/3, которую можно представить только в виде периодической дроби.

Часто случается также, что дроби, которые являются конечными в одной системе счисления, становятся бесконечными в другой системе счисления. Например, дробь 1/10 явно имеет конечное десятичное представление 0.1, но, будучи переведена в двоичную систему счисления, становится бесконечной дробью 0.000110011001100.... Вычисляя сумму десяти чисел, каждое из которых будет представлять собой двоичное приближение к десятичной 0.1, мы в сумме не получим точно 1. Известно, что начинающие программисты иногда приходят в замешательство, сталкиваясь впервые с такими «чудесами». Трудность эта неизбежна, но легко преодолима.

4.4. Ошибки ограничения

Те ошибки, которые содержатся в исходной информации, определяют точность результата вычислений независимо от того, каким методом эти вычисления проводятся. Два других типа ошибок – ошибки ограничения и ошибки округления – определяются теми численными методами, которые были использованы для решения задачи. Например, общеизвестный бесконечный ряд Тейлора для синуса может использоваться для вычисления синуса любого угла х, выраженного в радианах. Конечно, невозможно использовать все члены ряда для вычислений, так как ряд бесконечен; вычисления ограничиваются конечным числом членов: например, до х⁷ или x⁹. Отброшенные члены ряда (а их число бесконечно) вносят некоторую ошибку в результат вычислений. Эта ошибка называется ошибкой ограничения, так как она возникает в результате ограничения бесконечного математического процесса.

Очень многие процессы, используемые при вычислениях, являются бесконечными, так что анализ ошибок ограничения очень важен.

4.5. Ошибки округления

Даже если предположить, что исходная информация не содержит никаких ошибок и все вычислительные процессы конечны и не приводят к ошибкам ограничения, то все равно в этом случае присутствует третий тип ошибок – ошибки округления. Предположим, что вычисления производятся на машине, в которой каждое число представляется пятью значащими цифрами, и что необходимо сложить два числа 9.2654 и 7.1625, причем эти два числа являются точными. Сумма их равна 16.4279, она содержит шесть значащих цифр и не помещается в разрядной сетке нашей гипотетической машины. Поэтому шестизначный результат будет округлен до 16.428, и при этом возникает ошибка округления. Так как вычислительные машины всегда работают с конечным количеством значащих цифр, то потребность в округлении возникает довольно часто.

Вопросы округления относятся только к действительным числам. При выполнении арифметических операций с целыми числами потребность в округлении не возникает. Сумма, разность и произведение целых чисел сами являются целыми числами; если результат слишком велик, то это свидетельствует об ошибке в программе и результат при этом не округляется. Частное от деления двух целых чисел не всегда является целым числом, но деление двух целых чисел всегда выполняется таким образом, что дробная часть просто игнорируется. Кроме того, в подавляющем большинстве научных и инженерных расчетов деление целых чисел вообще не используется.

Поскольку будет рассматриваться округление действительных чисел, необходимо вспомнить форму их записи и договориться о некоторых условностях. Напомним, что действительное число можно представить в виде дроби, которую часто также называют мантиссой, умноженной на целую степень 10, называемую порядком. Например:

0.7392∙10⁴ ( = 7392.),

0.3246∙10² ( = 32.46),

0.1627∙10^-3 ( = 0.0001627).

Действительное число называется нормализованным, если первая значащая цифра мантиссы не равна нулю. В дальнейшем мы будем предполагать, что все действительные числа нормализованы.

Если обозначить мантиссу действительного числа х через f, а его порядок через е, то в общей форме число запишется следующим образом:

x = f^.10^e.

Величина f не может быть меньше 1/10, так как все числа должны быть нормализованными; эта величина не может также быть больше 1, так как мантисса должна быть правильной дробью.

Результат выполнения арифметической операции в общем случае состоит из двух частей: старшей и младшей. Например, предположим, что необходимо сложить два действительных числа и что в ячейке памяти вычислительной машины мантисса может представляться четырьмя значащими цифрами, а порядок – одной цифрой:

0.1624∙10³(= 162.4),

0.1769∙10¹ (= 1.769).

ЭВМ автоматически выравнивает порядки действительных чисел при сложении и вычитании. Это означает, что порядки сначала сравниваются, а затем мантисса меньшего по абсолютной величине числа сдвигается вправо на столько разрядов, сколько необходимо для того, чтобы порядки стали одинаковыми. В нашем случае получается следующий результат:

0.1624∙10³ ,

0.001769∙10³.

Другими словами, мантисса числа с меньшим порядком сдвигается вправо на число разрядов, равное разности между порядками. Теперь можно непосредственно сложить две мантиссы.

Очевидно, что сумма будет иметь больше четырех значащих цифр в мантиссе. Результат до округления можно представить в виде суммы двух действительных чисел:

0.1624∙10³ ,

0.001769∙10³,

0.164169∙10³ =0.1641∙10³+ 0.6900∙10^-1.

Любая из четырех арифметических операций даст в результате число, которое можно представить в виде двух аналогичных слагаемых. В общем виде перед округлением результат арифметической операции можно записать так:

y = f_y∙10^e + g_y∙10^e-t

Здесь f_y имеет t значащих цифр. Диапазон возможных значений f_y, как мы условились, лежит между 0.1 и 1.0 (0.1 ≤ f_y < 1.0). Для g_v это не так, потому что g_y может и не быть нормализованным числом; в частности, g_v может оказаться равным нулю. Для g_v диапазон возможных значений составляет 0 ≤ g_y<. 1.0.

Теперь мы подходим к двум вопросам первостепенной важности: согласно каким правилам следует учитыватьвеличинуg_y при изменении f_y и какова максимально возможная ошибка округления величины у для каждого из таких правил?

Обычно «округление» означает, что с величиной f_y производится какое-то действие, зависящее от величины g_y. В общем случае необходимо рассматривать и такую возможность, когда никакого действия не производится, т. е. когда g_y просто отбрасывается. Соответствующий метод округления называется отбрасыванием младших разрядов.

Некоторые трансляторы организованы таким образом, что рабочие программы, составленные с их помощью, используют правило отбрасывания g_y. Этот способ округления вносит большие ошибки, чем обычное округление (так называемое симметричное округление). С другой стороны, если использовать обычное правило округления при выполнении каждой арифметической операции даже там, где в нем нет никакой необходимости, то это приводит к неоправданным затратам машинного времени. Поэтому многие составители программ-трансляторов резонно решили, что уменьшение точности, вызванное отбрасыванием, достаточно мало и не перевешивает тех выгод, которые приобретаются в результате упрощения рабочих программ и экономии машинного времени.

При использовании правила отбрасывания максимальная относительная ошибка округления действительного числа не зависит от величины этого числа, а зависит только от количества значащих цифр в ячейке памяти ЭЦВМ. Таким образом, получается твердая оценка величины относительной ошибки для вычисле­ний с действительными числами.

Интересно и важно отметить тот факт, что ошибка округления не накапливается при использовании итерационных методов решения уравнений. Общая ошибка округления равна ошибке, возникшей в последней итерации, и не зависит от арифметических операций, выполнявшихся в предыдущих итерациях. Это общее свойство всех итерационных методов; оно является одним из важнейших преимуществ итерационных методов перед всеми другими. Причина того, что ошибки округления не накапливаются, ясна — каждое новое приближение, включая и предпоследнее, можно рассматривать как исходное приближение. Ошибка округления при вычислении последнего приближения зависит, таким образом, только от арифметических операций, с помощью которых это последнее приближение получается из предпоследнего.

4.6. Распространение ошибок

Одним из наиболее важных вопросов в численном анализе является вопрос о том, как ошибка, возникшая в определенном месте в ходе вычислений, распространяется дальше, т. е. становится ли ее влияние больше или меньше по мере того, как производятся последующие операции. Крайним случаем является вычитание двух почти равных чисел: даже при очень маленьких ошибках обоих этих чисел относительная ошибка разности может оказаться очень большой. Эта большая относительная ошибка будет распространяться. дальше при выполнении всех последующих арифметических операций.

В качестве первого шага при рассмотрении этого важного вопроса необходимо найти выражения для абсолютной и относительной ошибок результата каждого из четырех арифметических действий как функции величин, участвую­щих в операции, и их ошибок.

Для того, чтобы начать рассмотрение распространения ошибок, определим обозначения, которые мы будем использовать в этом разделе:

–точные значения,

–приближённые значения,

–абсолютная ошибка,

–количество значащих цифр.

Ошибки результата

Рассмотрим погрешности, которые вносятся в результат различных арифметических действий над числами x и y из-за наличия ошибок в определении этих чисел.

Сложение.

При сложении абсолютные ошибки складываемых чисел складываются

,

–относительная ошибка.

Вычитание.

При вычитании абсолютные ошибки чисел также вычитаются

.

Умножение.

При умножении ошибка каждого из перемножаемых чисел имеет свой вес, который определяется значением этого числа

Деление.

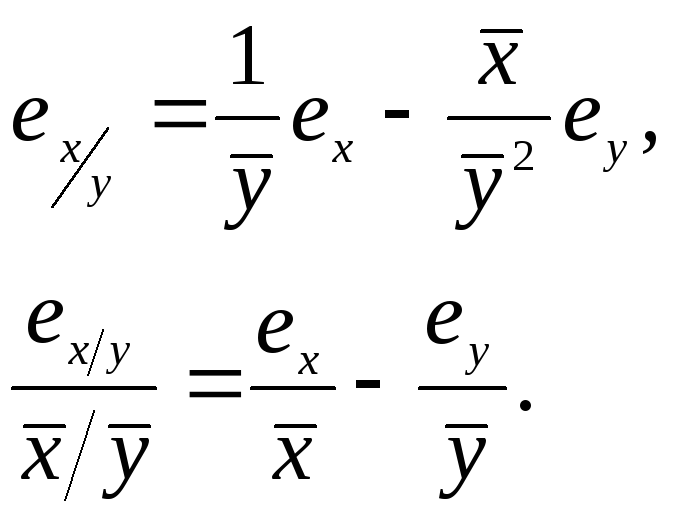
В качестве иллюстрации, которая может помочь наглядно представить себе смысл этих формул, рассмотрим сложение двух четырехзначных логарифмов. Так как оба логарифма точны до четвертого знака, то ошибка каждого из них не более 0.00005. Ошибка суммы не может быть больше 0.0001. Конечно, это не означает, что ошибка действительно столь велика, но означает только то, что ошибка может достигать такой величины.

Необходимо четко представлять себе, что знак ошибки бывает известен только в очень редких случаях. Не следует думать, например, что ошибка увеличивается при сложении и уменьшается при вычитании потому, что в формуле для сложения стоит плюс, а для вычитания – минус. Если, например, ошибки двух чисел имеют противоположные знаки, то дело будет обстоять как раз наоборот, т. е. ошибка уменьшится при сложении и увеличится при вычитании этих чисел.

Очень важно понимать смысл этих формул распространения ошибок. Мы начинаем арифметическую операцию, имея в своем распоряжении два приближенных значения х и у с соответствующими ошибками е_х и е_у. Ошибки эти могут быть любого происхождения. Величины х и у могут быть экспериментальными результатами, содержащими ошибки; они могут быть результатами предварительного вычисления согласно какому-либо бесконечному процессу и поэтому могут содержать ошибки ограничения; они могут быть результатами предшествующих арифметических операций и могут содержать ошибки округления. Естественно, они могут также содержать в различных комбинациях и все три вида ошибок.

Вышеприведенные формулы дают выражение ошибки результата каждого из четырех арифметических действий как функции от х, у, е_х, е_у; ошибка округления в данном арифметическом действии при этом не учитывается. Если же в дальнейшем необходимо будет подсчитать, как распространяется в последующих арифметических операциях ошибка этого результата, то необходимо к вычисленной по одной из четырех формул ошибке результата прибавить отдельно ошибку округления.

Проиллюстрируем распространение ошибки на конкретном примере. Предположим, что перед началом вычислений имеются три числа х, у и z, и для упрощения вопроса предположим, что исходные числа не содержат никаких ошибок. Необходимо вычислить

и = (х + у)z.

Согласно тому, как написано выражение, сначала должно быть выполнено сложение. Оба слагаемых не содержат никаких ошибок, поэтому ошибка, распространяющаяся через сложение, равна нулю; однако при выполнении операции сложения будет введена ошибка округления. Эта ошибка округления уже будет содержаться в сумме перед началом выполнения операции умножения.

Рассмотренные виды ошибок можно свести к минимуму, если выполнять следующие правила:

1. если необходимо произвести сложение — вычитание длинной последовательности чисел, работайте сначала с наименьшими числами;

2. если возможно, избегайте вычитания двух почти равных чисел. Формулы, содержащие такое вычитание, часто можно преобразовать так, чтобы избежать подобной операции;

3. выражение вида а(b-с) можно написать в виде аb-ас, а выражение вида (b-с)/а можно написать в виде b/a-с/а. Если числа в разности почти равны друг другу, производите вычитание до умножения или деления. При этом задача не будет осложнена дополнительными ошибками округления;

4. в любом случае сводите к минимуму число необходимых арифметических операций.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Алексеев, В.Е.Вычислительная техника и программирование: Практикум по программированию / В.Е.Алексеев; под ред. А.В. Петрова. – М.: Высшая школа, 1991. – 400 с.

2. Боглаев, Ю.П. Вычислительная математика и программирование: учебное пособие / Ю.П. Боглаев. – М.: Высшая школа, 1990. – 543 с.

3. Горинштейн, А.М. Практика решения инженерных задач на ЭВМ / А.М. Горинштейн.– М.: Радио и связь, 1984. – 232 с.

4. Дьяконов, В.П. Справочник по алгоритмам и программам на языке бейсик для персональных ЭВМ: Справочник / В.П. Дьяконов. – М.: Наука. Гл. ред. физ.-мат. лит. 1989. – 239 с.

5. Заварыкин, В.М. Численные методы: учебное пособие / В.М. Заварыкин, В.Г. Житомирский, М.П. Лапчик. – М.: Просвещение, 1991. – 174 с.

6. Мак-Кракен, Д. Численные методы и программирование на Фортране / пер. с англ.: Б.Н. Казака; под ред. Б.М. Наймарка. – 2-е изд., стереотипное. – М.: Изд-во «Мир», 1977. – 584 с.

7. Мудров, А.Е. Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль / А.Е. Мудров. – Томск: РАСКО, 1991. – 272 с.

8. Плис, А.И. Лабораторный практикум по высшей математике: учебное пособие для втузов / А.И. Плис, Н.А. Сливина. – М.: Высшая школа, 1994. – 416 с.

9. Светозарова, Г.И. Практикум по программированию на языке бейсик: учебное пособие для студентов вузов / Г.И. Светозарова, Е.В. Сигитов, А.В. Козловский; Под ред. С.В. Емельянова. – М.: Наука, 1988. – 368 с.

30