Метод Ньютона обладает высокой скоростью сходимости. Обычно абсолютная точность решения достигается через 5–6 итераций.

Недостатком метода является необходимость вычисления на каждой итерации не только левой части уравнения, но и её производной.

Можно, несколько уменьшив скорость сходимости, ограничиться вычислением производной только на первой итерации, а затем вычислять лишь значения, не изменяя производной. Это алгоритм так называемого модифицированного метода Ньютона

. (1.10)

Метод Ньютона (1.9)–(1.10) можно использовать для уточнения корней в области комплексных значений , что необходимо при решении многих прикладных задач. В этом случае начальное приближение к корню необходимо выбирать комплексным.

4. Метод хорд

Рассматриваемый метод так же, как и метод дихотомии, предназначен для уточнения корня на интервале [a,b], на концах которого левая часть решаемого уравнения принимает разные знаки. Интервал[a,b] по-прежнему определяем графическим методом. Очередное приближение теперь в отличие от метода дихотомии берём не в середине отрезка, а в точке , где пересекает ось абсцисс прямая линия, проведённая через точкии(рис.1.7).

Рис. 1.7

В качестве нового интервала для продолжения итерационного процесса выбираем тот из двух [a, ] или [,b], на концах которого функция принимает значения с разными знаками.

Заканчиваем процесс уточнения корня, когда расстояние между очередными приближениями станет меньше заданной погрешности

.

Уравнение прямой линии, проходящей через точки и, запишем в общем виде

.

Коэффициенты k и c уравнения этой прямой определим из условий

Вычитая левые и правые части последних соотношений, получим

Точку пересечения прямой с осью абсцисс получим, приравнивая нулю

,

или

.

5. Метод секущих

Для нахождения решения с помощью данного метода необходимо задать начальные приближения и , расположенные достаточно близко друг к другу. В этом случае производнуюв алгоритме Ньютона можно заменить её приближённым значением в виде отношения приращения функций

к приращению аргумента

.

Таким образом, запишем формулу метода секущих

(1.11).

Геометрический смысл такого изменения алгоритма Ньютона в том, что от аппроксимации функции касательной мы переходим к секущей (рис.1.8).

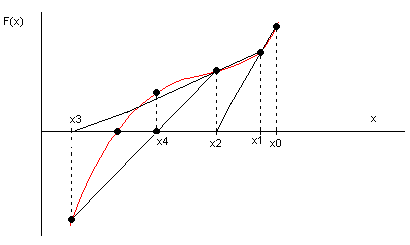
Рис. 1.8

Для того, чтобы начать итерационный процесс, необходимо задать два начальных приближения и. Затем каждое новое приближение получаем по формуле (1.11). Заканчиваем процесс уточнения корня при выполнении условия

,

где – заданная абсолютная погрешность определения корня.

Метод секущих несколько уступает методу Ньютона в скорости сходимости, однако не требует вычисления производной левой части уравнения.

2. Методы численного интегрирования

Вычисление определённых интегралов.

Методы численного интегрирования способны решать задачу приближённого вычисления определённого интеграла от заданной функции f(x) на заданном отрезке [a,b]:

. (2.1)

К численному интегрированию обращаются, когда нельзя через элементарные функции аналитически записать первообразную интеграла (2.1) или когда такая запись имеет сложный вид.

Сущность большинства методов вычисления определённых интегралов состоит в замене подынтегральной функции f(x) аппроксимирующей функцией , для которой можно записать первообразную в элементарных функциях, то есть

, (2.2)

где S – приближённое значение интеграла; R – погрешность вычисления интеграла.

Существует множество методов численного интегрирования. Рассмотрим некоторые из них.

1. Метод прямоугольников

Метод прямоугольников является одним из простейших методов численного интегрирования, когда подынтегральную функцию на интервале интегрирования заменяем полиномом нулевой степени, то есть константой. Подобная замена является неоднозначной, так как константу можно выбрать равной значению подынтегральной функции в любой точке в интервале интегрирования, поэтому метод прямоугольников обычно подразделяют на методы левых, правых и средних прямоугольников. Приближённое значение интеграла определится как площадь прямоугольника, одна из сторон которого есть длина отрезка интегрирования, а другая – аппроксимирующая константа.

Методы левых (рис.2.1) и правых (рис.2.2) прямоугольников, заменяющих интеграл нижней и верхней суммами Дарбу, имеют сравнительно высокую погрешность. На рис. 2.3 изображена графическая интерпретация метода средних прямоугольников.

Рис. 2.1

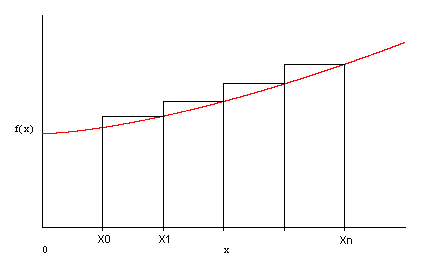
Рис. 2.2

Рис. 2.3

Запишем выражение для интеграла на интервале [], полученное методом средних прямоугольников:

, (2.3)

где ,, и оценим погрешностьR. Для этого разложим подынтегральную функцию f(x) в ряд Тейлора около средней точки :

, (2.4)

в малой окрестности точки этот ряд с высокой точностью представляет функцию f(x) при небольшом количестве членов разложения. Поэтому, подставляя под интеграл вместо функции f(x) её тейлоровское разложение (2.4) и интегрируя его почленно, можно вычислить интеграл с любой наперёд заданной точностью

(2.5)

При интегрировании и подстановке пределов получаем, что все интегралы от членов ряда (2.4), содержащих нечётные степени , обращаются в нуль.

Сравнивая соотношения (2.3) и (2.5), можно записать выражение для погрешности R. При малоё величине шага интегрирования h основной вклад в погрешность R будет вносить первое слагаемое, которое называется главным членом погрешности R вычисления интеграла на интервале []

.

Главный член полной погрешности для интеграла на всём интервале [] определяется путём суммирования погрешностей на каждом частичном интервале []:

. (2.6)

К последнему интегралу в формуле (2.6) мы перешли, используя метод средних прямоугольников для функции .

Формула (2.6) представляет собой теоретическую оценку погрешности вычисления интегралов методом средних прямоугольников. Степень шага h, которой пропорциональна величина R, называется порядком метода интегрирования. Метод средних прямоугольников имеет второй порядок.

Аналогично проведём оценку метода левых прямоугольников. Разложим подынтегральную функцию в ряд Тейлора около точки

(2.7)

Интегрируя разложение (2.7) почленно на интервале [], получим

,

где первое слагаемое есть приближённое значение интеграла, вычисленное по методу левых прямоугольников, второе слагаемое является главным членом погрешности

. (2.8)

На интервале [] главный член погрешности интегрирования получим суммированием частичных погрешностей (2.8)

. (2.9)

Таким образом, метод левых прямоугольников имеет первый порядок; кроме того, погрешность будет больше по сравнению с методом средних и за счёт интеграла от производной , и коэффициента в знаменателе (2.9).

2. Метод трапеций

Подынтегральную функцию заменим на участке [] полиномом первой степени. Как и в методах прямоугольников, такая аппроксимация неоднозначна. Одним из возможных способов является проведение прямой через значения функции на границах интервала интегрирования (рис. 2.4). В этом случае приближённое значение интеграла определяется площадью трапеции

.

Рис. 2.4

Погрешность метода трапеций получим путём интегрирования тейлоровского разложения подынтегральной функции около точки

, (2.10)

и интеграл

. (2.11)

С помощью выражения (2.10) вычислим подынтегральную функцию в точке

,

откуда

. (2.12)

Подставляя произведение (2.12) в выражение (2.11), получим

.

Следовательно, главный член погрешности метода трапеций на одном интервале будет

. (2.13)

Если интегрирование проводится путём разбиения отрезка [] на несколько интервалов, то общую погрешность получим суммированием частичных погрешностей (2.13)

. (2.14)

Как видно из выражения (2.14), метод трапеций, как и метод средних прямоугольников, имеет второй порядок. Если подынтегральная функция задана аналитически, то предпочтительнее из методов второго порядка применять метод средних прямоугольников вследствие его меньшей погрешности.

3. Метод Симпсона.

Подынтегральную функцию f(x) заменим на отрезке [] полиномом второй степени – параболой, проходящей через точки,,, тогда

,

где R – погрешность вычисления интеграла.

Для записи полинома воспользуемся интерполяционной формулой Ньютона

, (2.15)

где

разделённые разности, h – расстояние между узлами.

Введём новую переменную , тогдаи полином (2.15) принимает вид

. (2.16)

Теперь вычислим интеграл от полинома (2.16)

. (2.17)

Последнее соотношение называют квадратурной формулой Симпсона, или формулой парабол. Обобщим данную формулу для нахождения интеграла на отрезке [] при разбиении его на n частей с интервалом

,

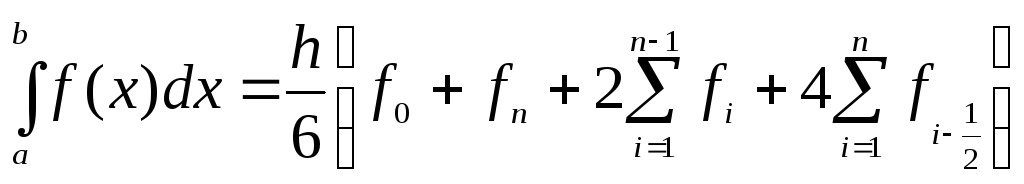где

.

Оценка погрешности формулы Симпсона производится аналогично оценкам погрешности для методов прямоугольников и трапеций. В результате получаем формулу

.

Следовательно, формула Симпсона имеет четвёртый порядок точности с очень малым численным коэффициентом в остаточном члене. Формула Симпсона позволяет получить высокую точность, если четвёртая производная подынтегральной функции не слишком велика.

2.4. Вычисление определённых интегралов с заданной точностью

Для обеспечения требуемой точности при приближённом вычислении значения интеграла нужно выбрать соответствующее число шагов n, на которое делится отрезок интегрирования. Для оценки погрешности в каждом из методов существуют формулы остаточных членов, однако, их использование в практике вычислений вызывает большие трудности.

На практике для достижения требуемой точности вычисления интеграла по формуле прямоугольников, трапеций или Симпсона часто используют метод последовательного удвоения числа шагов (“метод двойного пересчёта”), который заключается в следующем.

Интеграл вычисляется по выбранной формуле: сначала при числе шагов, равном n, а затем при числе шагов, равном 2n. Погрешность вычисления значения при числе шагов, равном 2n, определяется приближённо по формуле Рунге:

(для формул прямоугольников и трапеций , а для формулы Симпсона).

Таким образом, интеграл вычисляется для последовательных значений числа шагов ,и т.д., где– начальное число шагов. Процесс исчислений заканчивается, когда для очередного значенияN будет выполнено условие , где– заданная точность.

2.5. Вычисление несобственных интегралов

Известно несколько приёмов вычисления разных типов несобственных интегралов. Довольно распространённым является способ образования верхнего предела интегрирования, при котором исходный несобственный интеграл разбивается на сумму двух интегралов

.

Затем оценивается аналитически, а иногда и численными методами модуль второго интеграла и при выполнении условия

в качестве приближённого значения несобственного интеграла выбирается величина интеграла в пределах .

2.6. Погрешности

Формулы, выведенные для определения погрешности вычисления определённых интегралов различными методами, часто оказываются громоздкими и неудобными в использовании. В этом случае выводят более простые формулы, которые определяют максимальную погрешность вычисления интеграла. Для методов левых прямоугольников, трапеций и метода Симпсона эти формулы имеют следующий вид:

где – погрешность представления чисел (для чисел типаfloat , для чисел типаdouble ),n – количество промежутков разбиения,

.

2.7. Особенности итерационных методов

При разработке программ следует учесть, что в итерационных алгоритмах поиска решения с заданной точностью может возникать «зацикливание», т. е. вычислительный цикл не заканчивается за приемлемое время счета, либо вообще становится бесконечным, например для методов Ньютона, простых итераций и им подобных. Для избежания подобной ситуации необходимо в алгоритме предусмотреть ограничение на максимальное число итераций, по достижении которого происходит выход из цикла расчета с выдачей соответствующего сообщения. Например, можно поместить расчетный алгоритм внутри цикла с заданным числом повторений. Максимально допустимое число итераций зависит от применяемого метода расчета, желаемой точности вычислений и его можно взять с запасом. Например, для быстро сходящихся методов типа метода Ньютона это десятки итераций, для медленных типа половинного деления это количество может достигать сотен и тысяч. В любом случае, для итерационных алгоритмов поиска решения с заданной точностью максимальное число итераций необходимо ограничить.

3. Решение систем линейных алгебраических уравнений