1.12 Метрологические характеристики средств измерений

Технические характеристики СИ, оказывающие влияние на результаты и погрешности измерений называются метрологическими характеристиками. Метрологические характеристики СИ нормируются в государственных стандартах или в ТУ.

Основными метрологическими характеристиками являются предел измерений и погрешность измерения.

Под абсолютной погрешностью измерительного прибора понимают разность между его показанием Х_п и действительным значением Х_д измеряемой величины:

.

Однако в большей степени точность измерительного прибора характеризуется относительной погрешностью, т.е. выраженным в процентах отношением абсолютной погрешности к действительному значению измеряемой величины:

.

Если диапазон измерения прибора охватывает и нулевое значение измеряемой величины, то относительная погрешность обращается в бесконечность, в соответствующей точке шкалы. В этом случае пользуются понятием приведенной погрешности, равной отношению абсолютной погрешности прибора к некоторому нормирующему значению Х_н:

.

В качестве нормирующего значения принимается значение, характерное для данного вида измерительного прибора (диапазон измерений, верхний предел измерений, длина шкалы и т.д.). Правила выбора нормирующего значения устанавливаются ГОСТ 8.009-84 «ГСИ. Нормируемые метрологические характеристики средств измерений».

Погрешности СИ принято подразделять на статические и динамические. Статические в свою очередь, подразделяются на систематические и случайные.

При нормировании погрешностей СИ указывают либо систематическую и случайную составляющие погрешности (как правило для эталонов и некоторых особо точных СИ), либо указывают предельные значения допускаемых погрешностей (абсолютной или относительной).

1.13 Классы точности си

Классом точности называется обобщенная характеристика средства измерения определенного типа, отражающая уровень его точности, выражаемая характеристиками, влияющими на точность.

Для установления классов точности средств измерений применяют правила, содержащиеся в ГОСТ 8.401-80 «ГСИ. Классы точности средств измерений. Основные положения». В соответствии с этими правилами производится гарантированная оценка границ погрешности средства измерений.

Классы точности устанавливаются в стандартах, технических условиях, содержащих определенные требования к тем или иным типам средств измерений. Если СИ, предназначено для измерения нескольких величин, то класс точности определяется для каждой из величин. Так же определяется класс точности для средств измерений, имеющих несколько диапазонов – для каждого диапазона устанавливается свой класс.

Присваиваются классы точности СИ при их разработке, в ходе проведения государственных приемочных испытаний. В процессе эксплуатации СИ, по результатам поверки или калибровки класс точности СИ может быть понижен.

1.14 Определение погрешности средств измерений по классу

точности

Форма представления класса точности СИ определяется пределами допускаемой основной погрешности измерений. В некоторых случаях вместе с основной нормируются пределы допускаемой погрешности, форма представления основной и дополнительной погрешностей может быть различна.

Пределы допускаемых погрешностей выражаются границами абсолютной погрешности СИ.

Сама форма представления класса точности пределами допускаемой основной абсолютной погрешности применяется преимущественно для мер массы или длины. Класс точности измерительных приборов в большинстве случаев выражается пределами допускаемой основной приведенной или относительной погрешности. При этом основой, для определения формы представления класса точности прибора, является характер изменения основной абсолютной погрешности средства измерений.

Характерные следующие случаи изменения границ абсолютных погрешностей средств измерений.

1 Если основная абсолютная погрешность имеет аддитивный характер, т.е. границы погрешностей измерительного прибора не изменяются в пределах диапазона измерений (рис. 4а), то класс точности представляется пределами допускаемой приведенной погрешности γ (%):

(1)

где  = а– пределы допускаемой основной абсолютной погрешности прибора;

р– отвлеченное положительное число, выбираемое из ряда чисел, указанного ниже;

X_N– нормирующее значение, выраженное в единицах абсолютной погрешности.





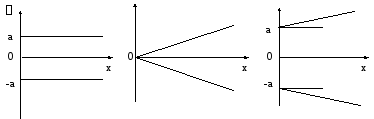
а б в

Рисунок 4 – Характерные случаи изменения границ

абсолютных погрешностей СИ

2 Если основная абсолютная погрешность имеет мультипликативный характер, т.е. границы погрешностей измерительного прибора линейно изменяются в пределах диапазона измерений (рис. 4б), то класс точности представляется пределами допускаемой относительной погрешности (%), в виде

(2)

где  = bx– пределы допускаемой основной абсолютной погрешности прибора (b = tg);

x– показания прибора (без учета знака измеренной величины);

q– отвлеченное положительное число.

3 Если основная абсолютная погрешность имеет и аддитивную и мультипликативную составляющие (рис. 4в), то класс точности представляется пределами допускаемой относительной погрешности (%), в виде

(3)

где  = (a+bx);

cиd – отвлеченные положительные числа.

Положительные числа p, q, c, d выбираются из установленного ряда: 110ⁿ; 1,510ⁿ; 2,010ⁿ; 2,510ⁿ; 410ⁿ; 510ⁿ; 610ⁿ (n = 1; 0; -1; -2; -3и т.д.)

На практике редко встречается, когда абсолютная погрешность чисто аддитивна или чисто мультипликативна. Поэтому класс точности в виде формул для первого и второго случаев устанавливается в тех случаях когда соответствующими погрешностями можно принебречь.