1.10 Основные характеристики случайной величины

В общем случае вероятность появления случайной погрешности находится в пределах от 0 до 1. Числовое значение какой – либо погрешности нельзя предвидеть заранее. Но зная закон распределения случайной погрешности можно установить вероятность появления каких-либо ее значений, а следовательно, и вероятность появления каких-либо значений измеряемой величины.

Основными числовыми характеристиками результата измерений и его погрешности являются:

- среднее арифметическое значение измеряемой величины;

D_x - дисперсия случайной величины;

- среднее квадратичное отклонение (СКО).

Положение центра группирования случайной величины определяется математическим ожиданием.

Статистической оценкой математического ожидания является среднее арифметическое:

,

x₁, x₂,….x_n – действительные значения измеряемой величины;

n – число измерений.

Основными числовыми характеристиками рассеивания случайной величины относительно центра группирования являются ее дисперсия и среднее квадратичное отклонение.

Дисперсия D_x служит мерой рассеивания значений случайной величины Х около центра группирования, но ее размерность выражается квадратом размерности случайных величин

.

Поэтому в качестве меры рассеивания значений случайной величины часто применяют СКО ()

.

СКО имеет ту же самую размерность, что и случайные величины.

Статистической оценкой СКО является так называемое стандартное отклонение:

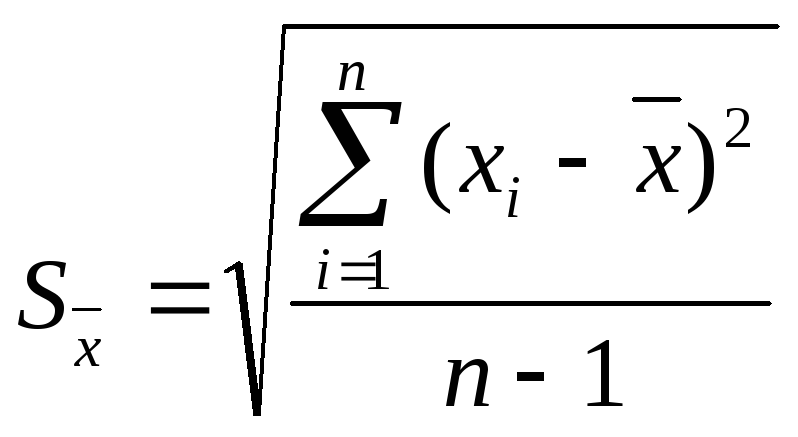
Стандартное отклонение характеризует ширину области рассеивания значений случайной величины. Чем меньше ширина области рассеивания, тем точнее проведены измерения, и наоборот.

Результат многократных измерений записывается в форме доверительного интервала

где t – относительный доверительный интервал, определяемый по формуле

.

Относительный доверительный интервал t находится в зависимости от заданной доверительной вероятности. Если при этом установлено, что закон распределения вероятности результатов измерения - нормальный, то для нахождения относительного доверительного интервала по доверительной вероятности (и наоборот, доверительной вероятности по относительному доверительному интервалу) используются математические таблицы специальной функции Лапласа.

1.11 Алгоритм обработки многократных измерений

1 Анализируют результаты измерений, исключают систематические погрешности из результатов измерений, внося поправки.

2 Вычисляют - среднее арифметическое значение измеряемой величины. Полученную величину принимают за результат измерения.

3 Вычисляют стандартное отклонение

4 Определяют и исключают грубые промахи.

В группе результатов наблюдений иногда встречаются результат(ы), значительно отличающиеся от всей группы. Наиболее подозрительными являются минимальное и максимальное значения. Их, как правило, исключают из эксперимента. Вопрос о том, содержит ли данный результат грубую погрешность, решается общими методами проверки статистических гипотез.

Проверяемая гипотеза состоит в утверждении, что результат х_i не содержит грубой погрешности. Для проверки этой гипотезы используют распределения следующих величин:

Эти функции совпадают между собой, и для нормального распределения результатов измерения они протабулированы. По таблицам при заданной доверительной вероятности Р и количестве измерений n находят табличное (предельно допустимое) значение _т; его сравнивают с расчетным значением _р. Если выполняется условие _р  _т , то гипотеза об отсутствии грубой погрешности принимается с вероятностью Р. Если условие не выполняется, то минимальное и (или) максимальное показания исключаются из результатов измерения и процедура повторяется.

Иногда грубые погрешности исключаются с помощью правила «трех сигм». Если известно, что закон распределения - нормальный, и его числовые характеристики (их оценки) равны и, то с доверительной вероятностью 0,9973 грубыми промахами являются те результаты измерения, которые выходят за границы интервала Мх  Sх.

После того, как грубые погрешности (промахи) исключены из результатов измерения, снова определяют оценки числовых характеристик и убеждаются в отсутствии грубых погрешностей.

5 Строят гистограмму и определяют вид закона распределения вероятности результата измерения.

При построении гистограммы распределения по оси абсцисс откладываются интервалы значений измеряемой величины (обычно равные), эти отрезки являются основаниями прямоугольников, площади которых равны частотам р* попадания значений величины на каждый интервал (р*= m/n, где m – количество результатов измерений, попавших в данный интервал). Таким образом, высота каждого прямоугольника равна частоте, деленной на длину интервала. Очевидно, что полная площадь гистограммы равна единице.

По виду гистограммы, а также исходя из существа задачи, можно предположить принципиальный вид кривой распределения (закона распределения вероятности). Например, из рис. 2 видно, что распределение вероятности, скорее всего окажется нормальным.

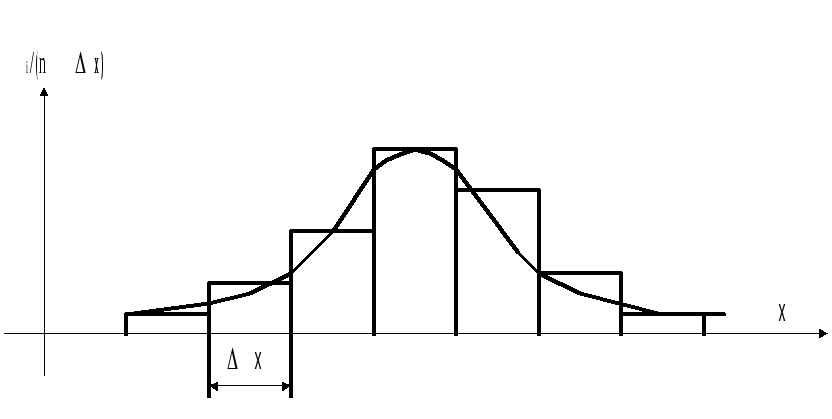
Рисунок 2 – Гистограмма

Для предполагаемого распределения с вычисленными оценками числовых характеристик строится теоретическая кривая. Далее следует выяснить вопрос, являются ли расхождения теоретического и статистического распределения случайными (из-за малого числа наблюдений), или объясняются неправильно подобранным теоретическим распределением? На этот вопрос отвечают с помощью так называемых критериев согласия; наиболее распространенным из них является критерий К.Пирсона.

6 Проверяют гипотезу о виде закона распределения, чаще всего о нормальности этого закона с помощью критерия Пирсона.

При использовании этого критерия за меру расхождения экспериментальных данных с теоретическим распределением принимается сумма квадратов отклонения теоретических вероятностей р_i от соответствующих частот m_i/n, взятых с некоторыми коэффициентами (весами) n/p_i :

где k - число интервалов гистограммы,

m_i - число результатов измерений, попавших в i-й интервал,

n - общее число наблюдений (измерений).

Если расхождение случайно, то величина ² подчиняется т.н. ² распределению Пирсона. Предельно допустимые значения критерияданы в таблицах. Если при заданной доверительной вероятности и числе степеней свободы r = k - 3 выполняется условие, то принимается гипотеза о соответствии распределения принятому закону, например, нормальному.

При использовании критериев согласия возможны два рода ошибок:

Ошибка первого рода состоит в том, что отвергается верная гипотеза.

Ошибка второго рода состоит в том, что принимается неверная гипотеза.

Вероятности и той, и другой ошибки зависят от значения , которое, в свою очередь, определяется вероятностью, с которой принимается решение. С повышением этой вероятности увеличивается значение(доверительный интервал), и, следовательно, вероятность ошибки первого рода уменьшается, а ошибки второго рода - возрастает, и наоборот. Таким образом, нецелесообразно принимать решение с очень высокой степенью вероятности. Обычно выбирается Р = 0,9...0,95.

7 Определяют ширину доверительного интервала на основании заданной доверительной вероятности.

Значение относительного доверительного интервала для среднего значения выбирается по заданной доверительной вероятности; при этом, если подтверждена гипотеза о нормальности распределения результатов наблюдений, то распределение среднего арифметического для ряда подобных совокупностей равноточных результатов также следует считать нормальным. В этом случае значение «t» выбирается из таблиц функции Лапласа. Если же согласно априорной информации закон распределения вероятности для среднего считается неизвестным, то для увязки доверительного интервала с доверительной вероятностью используют неравенство П.Л.Чебышева:

Для симметричных законов распределения неравенство Чебышева имеет вид: