Лекция № 6

Тема:

Частотные характеристики дискретных систем.

План лекции:

1. Определение установившейся реакции импульсной системы на дискретный гармонический сигнал.

2. Частотные характеристики дискретных систем.

3. Свойства частотных характеристик импульсных систем.

1. Определение установившейся реакции импульсной системы на дискретный гармонический сигнал.

Рассмотрим прохождение дискретного гармонического сигнала

.

через импульсную систему с передаточной функцией . Для этого найдем реакцию системы на воздействие

(31)

и далее выделим ее действительную часть,

Найдем изображение сигнала (31). На основании формулы (20) получим

.

Изображение выходной переменной системы имеет вид

.

Вычислив обратное Z-преобразование, найдем реакцию импуль­сной системы на сигнал (31):

где - особые точки выражения, стоящего под знаком вычета, т.е. это полюсы передаточной функциии точка.

Положим для простоты, что полюсы передаточной функциинекратные и удовлетворяют условию

(32)

Тогда

или

(33)

где

.

При выполнении условия (32) второе слагаемое правой части формулы (33) стремится к нулю при и в системе устанавливается вынужденное движение

(34)

Выделив в выражении (34) действительную часть, получим реакцию системы на гармонический сигнал в виде

.

Из последней формулы видно, что при прохождении дискретного гармонического сигнала через импульсную систему у него изменяются амплитуда и фаза: амплитуда увеличивается в раз, а фаза изменяется на.

2. Частотные характеристики дискретных систем.

Выражение , полученное изZ-передаточной функцииподстановкой, называется амплитудно-фазовой частотной характеристикой (АФЧХ) импульсной системы. Функцияназывается амплитудной частотной характеристикой, функция- фазовой частотной характеристикой импульсной системы. АФЧХ импульсной системы позволяют найти установившуюся реакцию на гармоническое воз­действие, и в этом они сходны с АФЧХ непрерывных систем. АФЧХ импульсных систем определяют по следующим формулам:

, (38)

, (39)

. (40)

Пример. Пусть . Найти частотные характеристики звена с такой передаточной функцией.

В соответствии с определением имеем

;

;

.

Графики АФЧХ, построенные по приведенным зависимостям, показаны на рис.17 (здесь).

Рис .17

Из рис.17 видно, что частотные характеристики импульсных систем существенно отличаются от АФЧХ непрерывных систем, изучаемых в курсе "Основы ТАУ".

3. Свойства частотных характеристик импульсных систем.

Рассмотрим некоторые свойства частотных характеристик импульсных систем.

1.Вследствие периодичности экспоненты частотная характеристика дискретной системы является периодической функцией частоты с периодом. Поэтому АФЧХ импульсной системы полностью определяется значениями в диапазоне(в основной полосе). Периодичность АФЧХ приводит к тому, что импульсная система одинаково пропускает сигналыи, так как в обоих случаях на выходе ИИЭ существуют одинаковые последовательности импульсов. Это свойство импульсных систем поясняет рис.18.

Р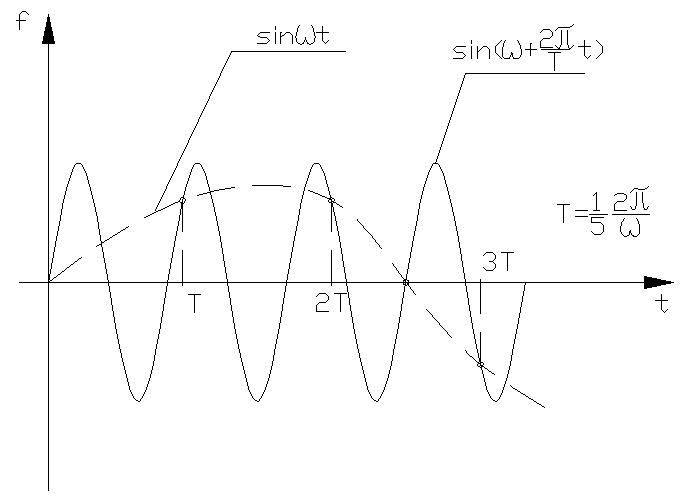ис. 18

2. Амплитудно-частотная характеристика является четной функцией частоты, т.е.

Вследствие четности АЧХ и периодичности достаточно знать значения АЧХ в диапазоне.

Фазово-частотная характеристика является нечетной функцией частоты, т.е..

Она также может быть задана своими значениями в диапазоне .

3. При частотах , гдечастотная характеристика дискретной системы всегда принимает действительные значения:

или

.

Это свойство выполняется за исключением случаев, когда передаточная функция ПНЧ имеет полюспорядка m .Тогда передаточная функция W(z) имеет полюс z=1 того же порядка m и при.