2. Учет экстраполятора при вычислении z- передаточных функций.

Однако предположение о том, что передаточная функция W(p) ПНЧ есть дробно-рациональное выражение, не всегда выполняется. Как отмечалось ранее

,

где передаточные функции формирователя и собствен­но непрерывной части соответственно. Если обычно явля­ется дробно-рациональной функцией, то будет таковой лишь при некоторых упрощающих предположениях (см. [4] ). Обычно является трансцендентной функцией p, например, для экстраполятора нулевого порядка

.

Рассмотрим этот случай и определим для него порядок нахождения Z-передаточной функции W(z). Пусть - дробно-рациональная функция

, (16)

где , - многочлены степени m и n соответственно. Пусть- полюсы передаточной функции (16). Счи­тая, что все полюсы первого порядка, разложим выражение (16) на простейшие дроби:

.

Тогда

или

.

В соответствии со свойствами -преобразования множитель может быть вынесен за знак преобразования (см. курс “Математические основы ТАУ” или [6,прил.2]). Тогда

(17)

Найдем . Очевидно, что

.

Пользуясь таблицей -преобразования с учетом теоремы линей­ности, получим

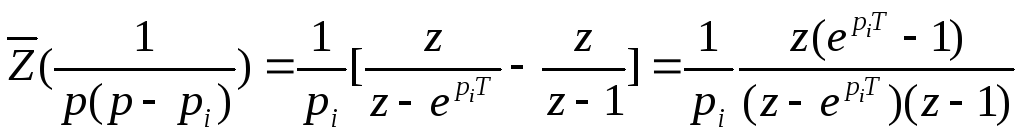(18)

Подставив выражение (18) в формулу (17), найдем

, (19)

т.е. получена формула для вычисления Z-передаточной функ­ции W(z) разомкнутой системы. Отметим, что при , а также при наличии кратных полюсов в формуле возникают неопре­деленности. Они могут раскрываться обычным способом, по прави­лу Лопиталя. Кроме того, формулу (17)) можно записать в виде

Здесь под знаком -преобразования стоит дробно-рацио­нальная функция. Определив так, как излагалось выше (исполь­зуя разложение выражения на простейшие дроби), можно легко найти Z -передаточную функцию разомкнутой системы.

В общем случае для определения Z-передаточной функции W(z)можно использовать зависимость, полученную ранее в курсе «Математические основы ТАУ»:

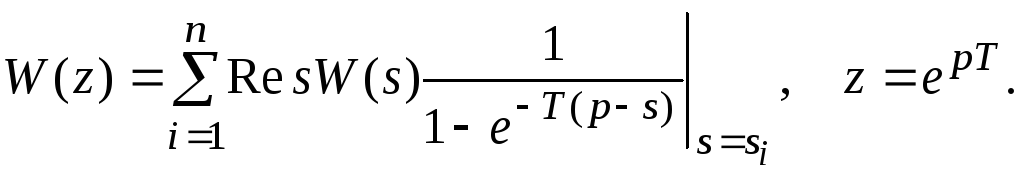(20)

где s_i– полюсы передаточной функцииW(s)ПНЧ ().

Следует, однако, иметь в виду, что формула (20) справедлива, если выполняется условие

(21)

Например, если передаточная функция ПНЧ имеет вид и степень многочленапревосходит степеньне менее чем на 2 порядка, то условие (21 выполняется, и тогда из зависимости (20) получим

(22)

В случае, если передаточная функция ПНЧ содержит выражение 1-е^-Tp, ее можно представить в виде

где - дробно-рациональная функция.

Тогда

и

(23)

где - полюсы функции.

3. Пример вычисления z –передаточной функции.

Найдем Z-передаточную функцию разомкну­той системы, состоящей из ИЭ с экстраполятором нулевого по­рядка и непрерывной части с передаточной функцией .

Передаточная функция ПНЧ имеет вид

.

Для нахождения W(z) применим формулу (23):

.

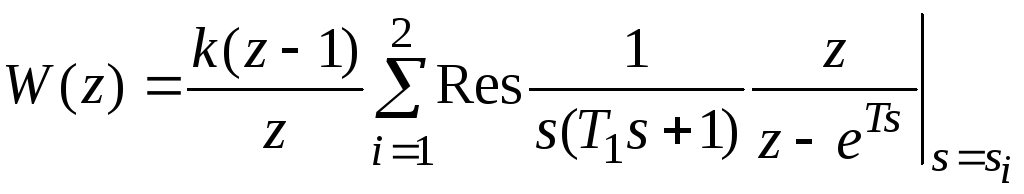Полюсы выражения следующие:.

Тогда получим

;

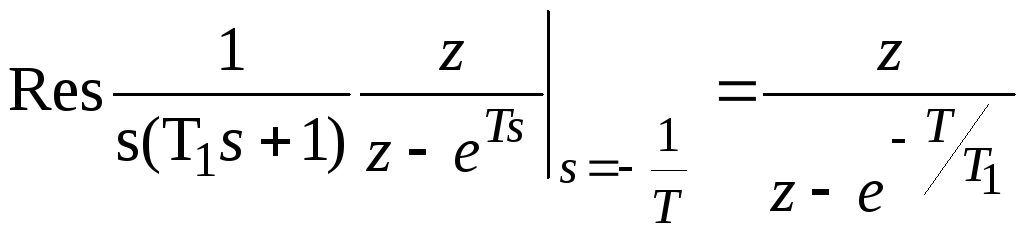
Отсюда следует

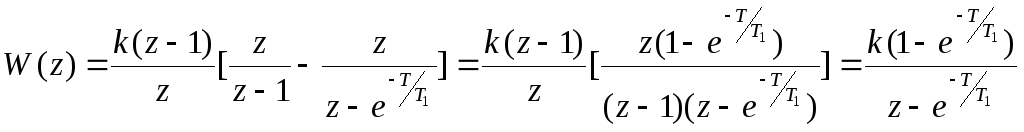
Этот же результат можно получить с помощью таблицы -преоб­разования, а именно

.

Проводя разложение на простейшие дроби, найдем

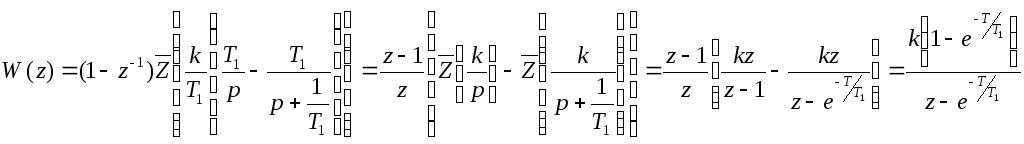
Отметим некоторые свойства Z-передаточных функций. Передаточная функция есть дробно-рациональная функция z. При использовании модифицированного Z-преобразования числитель этой функции зависит от . Порядком передаточной функцииназовем степень n ее знаменателя. Порядок дискретной передаточной функции равен степени знаменателя передаточной функции непрерывной части системы.

Полюсы Z-передаточных функцийисвязаны с полюсамипередаточной функциинепрерывной части и определяются соотношением

(24)

Рассмотрим задачу определения реакции дискретной системы с передаточной функцией на входной сигнал. Определив Z-преобразование входного сигнала, запишем уравнение системы в изображениях:

(25)

Таким образом, если Z-преобразование выходной величины известно, процесс на выходе может быть найден по формуле обратного Z-преобразования:

Для нахождения можно применить известную формулу

где - полюсы функций

Для вычисления обратного Z-преобразования, кроме того, может быть использовано разложение изображения в ряд Лорана [4]. Наконец, по известной Z-передаточной функции нетрудно составить соответствующее разностное уравнение импульсной системы. Пусть

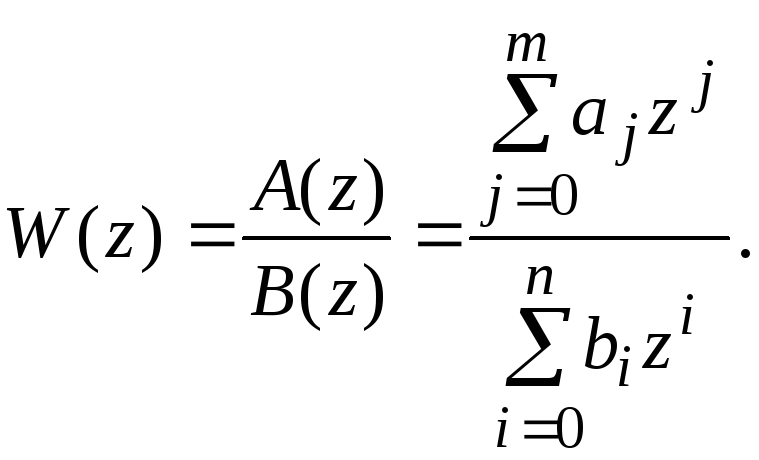
Тогда уравнение (25) можно переписать в виде

Переходя к оригиналам и учитывая теорему о смещении аргумента решетчатой функции, получим

Это соотношение представляет собой разностное уравнение системы, с помощью которого можно рассчитать процесс на выходе дискретной САУ.