3. Передаточная функция разомкнутой импульсной системы.

3апишем теперь уравнения разомкнутой системы в изображени­ях. Применим к зависимости (10) Z-преобразование, С учетом свойств Z-преобразования найдем

, (11)

где Y(z)=Z{y[nT]}, F(z)=Z{f[nT]},W(z)=Z{w[nT]}.

Определим Z -передаточную функцию импульсной системы как отношение Z -преобразования выходной величины к Z -преоб­разованию входной величины при нулевых начальных условиях:

.

Из уравнения (11) следует, что Z -передаточная функ­ция разомкнутой импульсной системы равна Z -преобразованию дискретной весовой функции w[nT] ПНЧ. т.е.

. (12)

Формула (12) используется при вычислении Z -передаточных функ­ций разомкнутых импульсных систем.

Иногда возникает необходимость определить реакцию системы в смещенные дискретные моменты времени . Подставив в зависимость (9), получим

(13)

Перейдя к уравнению в изображениях, найдем

(14)

Здесь изображения соответствуют модифицированномуZ-преобразованию решетчатых функций,. Уравнению (14) соответствует передаточная функция

,

cвязывающая модифицированноеZ-преобразование выходного сигнала и обычноеZ-преобразование входной переменной. При изменении параметра от 0 до 1 зависимости (13), (14) позволяют определить значение выходной величины в любой промежуточный момент времени.

Лекция № 4

Тема:

Вычисление z-передаточных функций.

План лекции:

1. -преобразование дробно-рациональных функций.

2. Учет экстраполятора при вычислении Z- передаточных функций.

3. Пример вычисления Z –передаточной функции.

1.-Преобразование дробно-рациональных функций.

Рассмотрим вычисление Z -передаточной функции простей­шего соединения (см рис 8 ). В соответствии с формулой (12) и свойствами Z -преобразования Z -передаточная функция w(z) может быть найдена по известной весовой функции ПНЧ w(t) или по ее передаточной функции W(p). Связь между передаточными функциями W(z) и W(p) задается-преобразованием с последующей заменой. Обозначим операцию выполнения-преоб­разования с заменойчерез. Тогда

(15)

Приведем таблицу -преобразования для некоторых часто встречающихся функций W(p) [l] .

W(p)	W(z)
	,
	,

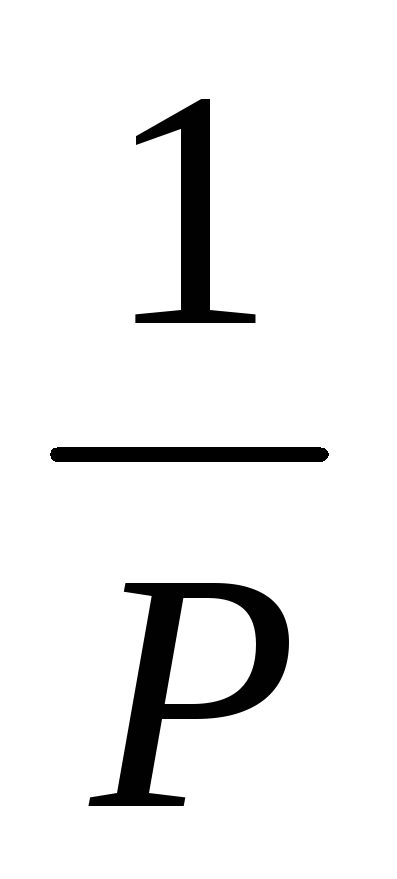
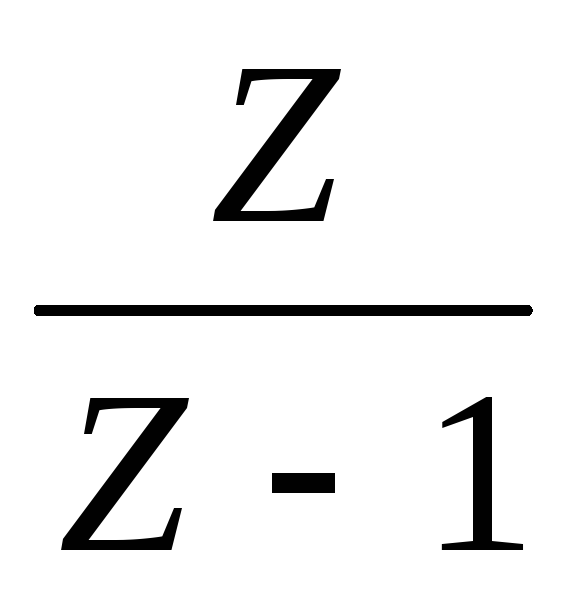
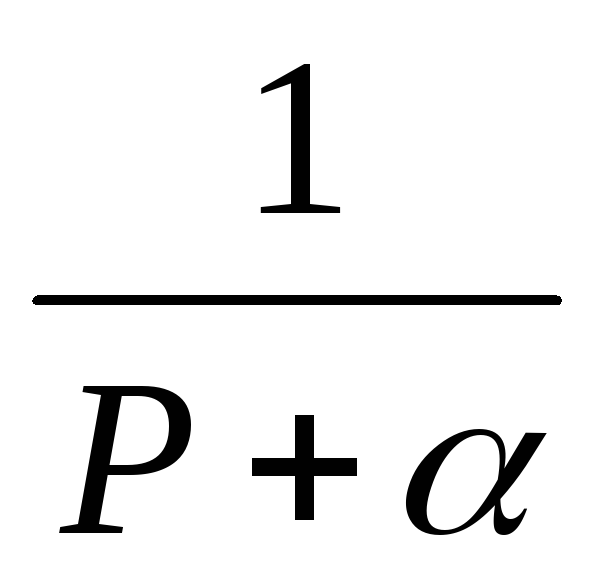
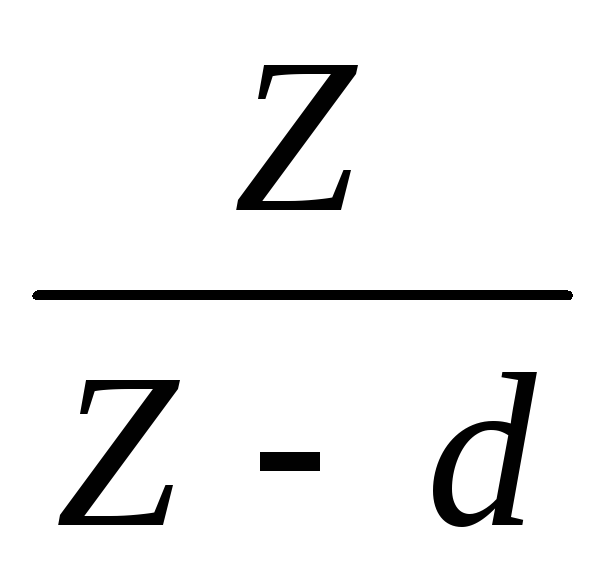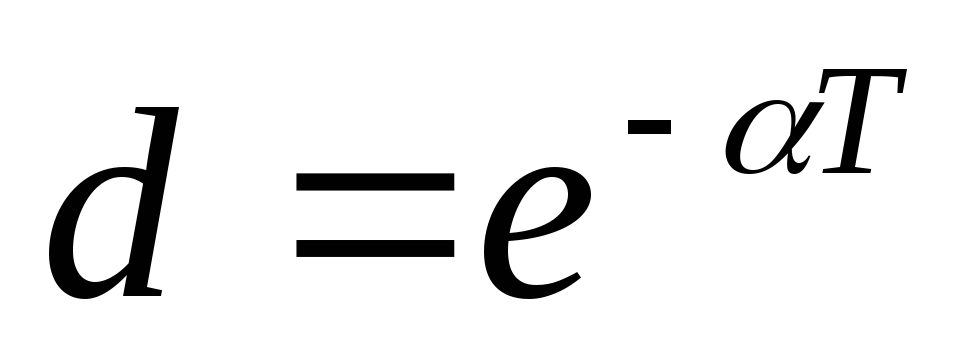
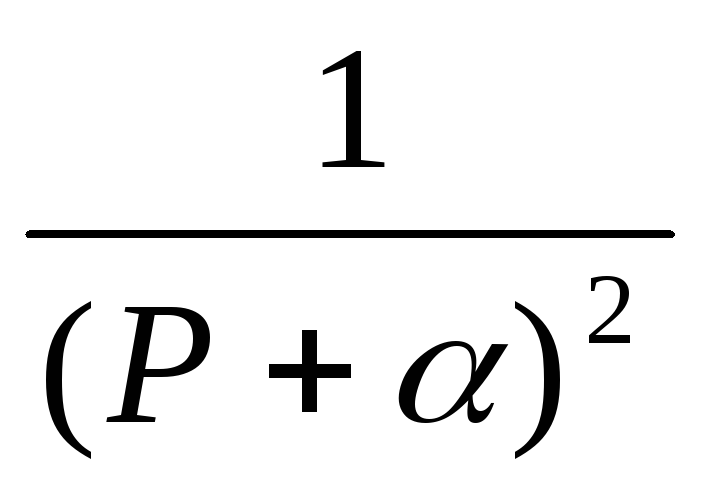
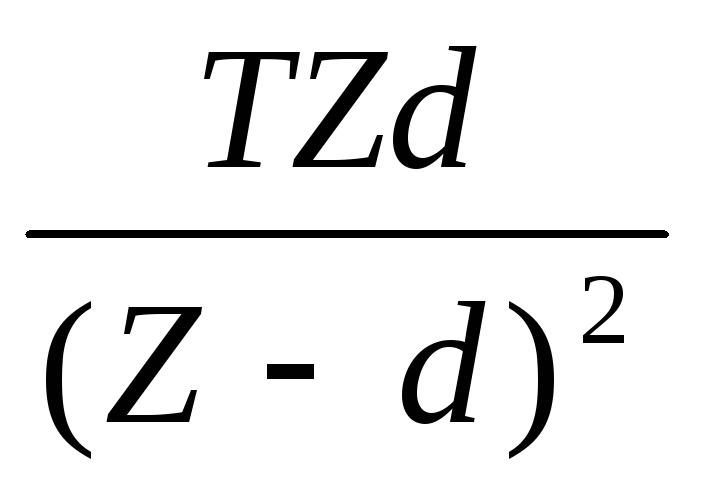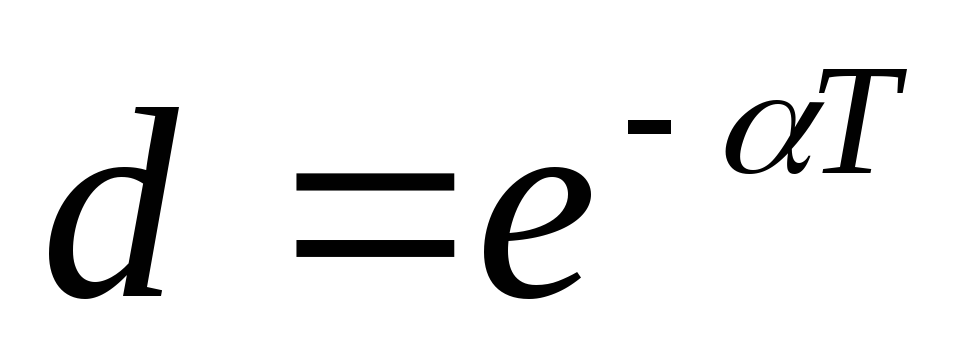
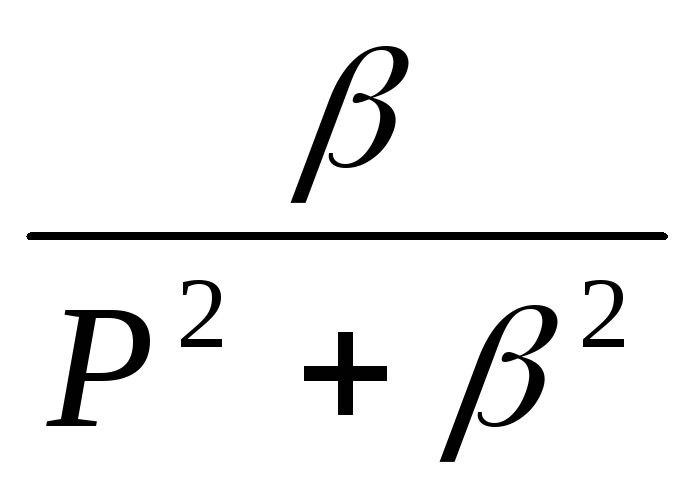
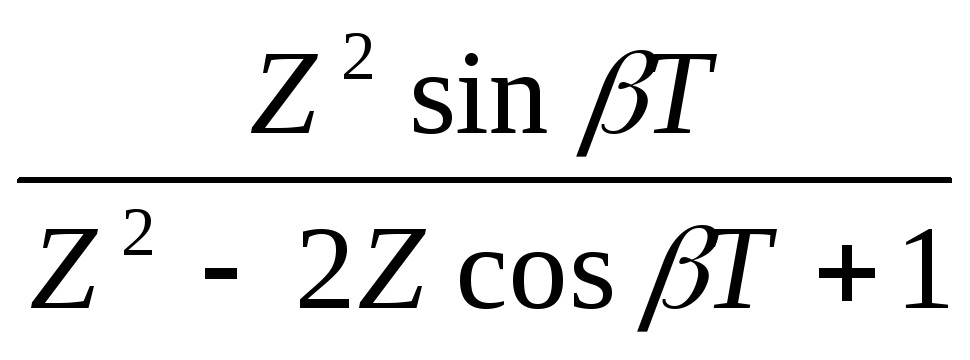
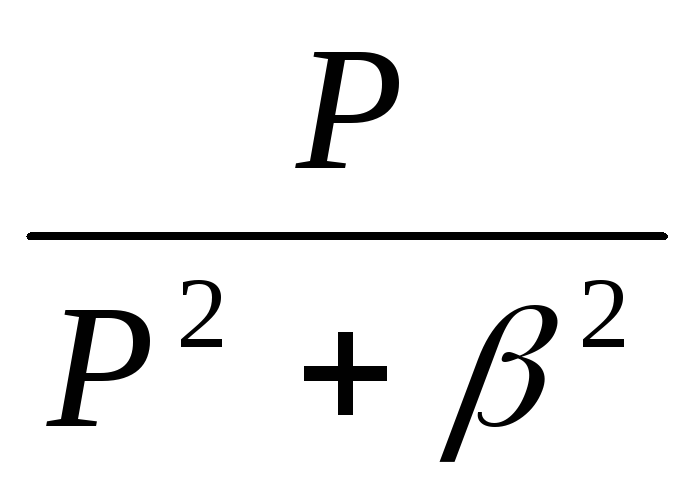
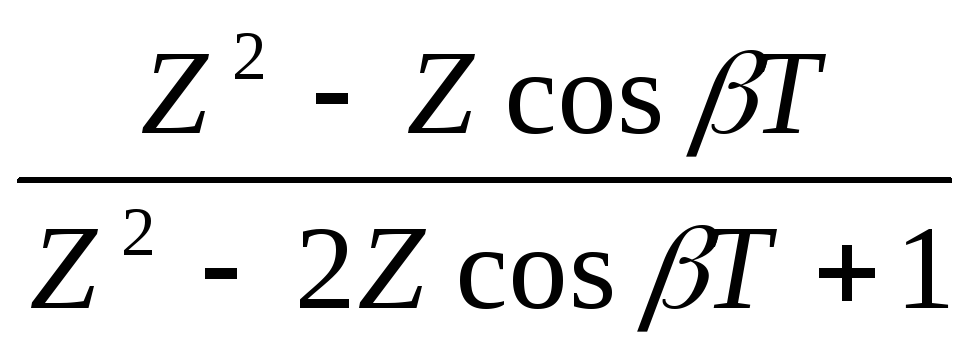
Так как - преобразование обладает свойством линейно­сти, то в случае, если W(p) - дробно-рациональное выражение, вычисление Z -передаточных функций можно проводить следующим образом:

Передаточную функцию W(p) разложить на простейшие дроби

.

2.Для каждой простейшей дроби с помощью таблицы найти- преобразование, т.е.

.

По теореме линейности -преобразования записатьи провести необходимые преобразования.