1. Обзор задач динамики.

Одной из основных задач динамики механических систем является задача определения управляющих сил по заданным свойствам движения. Задачи такого рода с различными их видоизменениями называют обратными задачами динамики. Обратные задачи динамики всегда привлекали к себе внимание, так как имеют широкие прикладные возможности.

Из возможных постановок обратных задач динамики рассмотрим задачу аналитического построения программного движения. При этом необходимо построить такую физическую систему, чтобы процессы в ней удовлетворяли заранее заданным свойствам. Назовем заданные свойства процесса программой движения, а весь процесс - программным движением рассматриваемой системы.

В конечном счете программное движение осуществляется действием на систему управляющих сил. Построение уравнений движения управляющих устройств составляет задачу аналитического построения замкнутых систем программного движения. При этом в задачу аналитического построения систем программного движения включаются как задачи установления осуществимости самой программы , так и задачи обеспечения устойчивости движения при наличии начальных отклонений переменных системы от их заданных значений.

2. Задача аналитического построения замкнутой системы программного движения.

В общем случае задачу аналитического построения замкнутой системы программного движения можно поставить таким образом

Уравнения движения объекта заданы и имеют вид

где х - вектор состояния системы, ; U- вектор управления. Требуется построить уравнение для вектора U в виде

так, чтобы программное движение с заданными свойствами являлось одним из возможных движений системы и было устойчивым по отношению к этим свойствам при наличии отклонений от них.

Рассмотрим класс следящих систем автоматического управления. В их задачу входит возможно более точное воспроизведение некоторого, обычно заранее неизвестного, входного сигнал. Задача формирования управления следящей системой может быть поставлена как задача аналитического построения системы программного движения. В литературе приведен ряд методов управления на основе решения обратной задачи динамики, но в них обычно рассматривается только свободное движение . Алгоритм управления, формируемый на основе решения обратной задачи динамики, позволяет oбеспечить высокое качество слежения за входным сигналом общего вида. Алгоритм реализуется с помощью ЦВУ, входящего в контур управления.

3. Синтез алгоритма управления на примере системы третьего порядка.

Рассмотрим синтез алгоритма управления на примере системы третьего порядка. Обобщение алгоритма на системы более высокого порядка не представляет сложности.

Пусть дифференциальное уравнение объекта имеет вид

(116)

где - скаляр - выходная переменная; U-управление.

На вход системы поступает сигнал ,который должен воспроизводиться переменной. Поставим задачу формирования управления

минимизирующего ошибку системы.

Введем интервал квантования T и будем стремиться к тому, чтобы в моменты времени t=kT,k=0,1,… выходной сигнал и его первая производная совпадали с входным сигналом и его первой производной. При этом управление строится отдельно на каждом временном отрезке . Пусть при t=kT известны величины x[kT],f[kT]. Предположим далее, что можно измерить или вычислить производную, а также , что в момент t=kT возможно экстраполировать функцию f(t) и оценить ее значение и значение ее первой производной при. Обозначим эти оценкии. Поставим задачу определения управления U(t) на отрезке, переводящего изображающую точку на плоскостииз начального положения, в конечное положение (,) .

Задачу определения управления будем решать как обратную задачу динамики , т.е. задавшись траекторией на плоскости соединяющей имеющуюся начальную и желаемую конечную точки, найдем управление U при. Зададимся следующим законом изменения координаты x(t) :

, (117)

где время t отсчитывается заново для каждого отрезка. Коэффициенты постоянны на каждом временном отрезке и изменяются при его смене.

Определим коэффициенты , исходя из начальных величини желаемых конечных величин,. Найдем производнуюсогласно формуле (117):

. (118)

Тогда система уравнений для определения коэффициентов примет вид

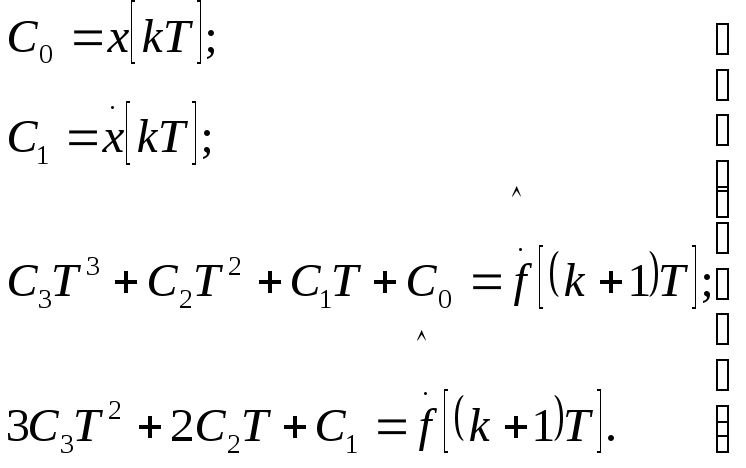(119)

Система (119) всегда имеет единственное решение

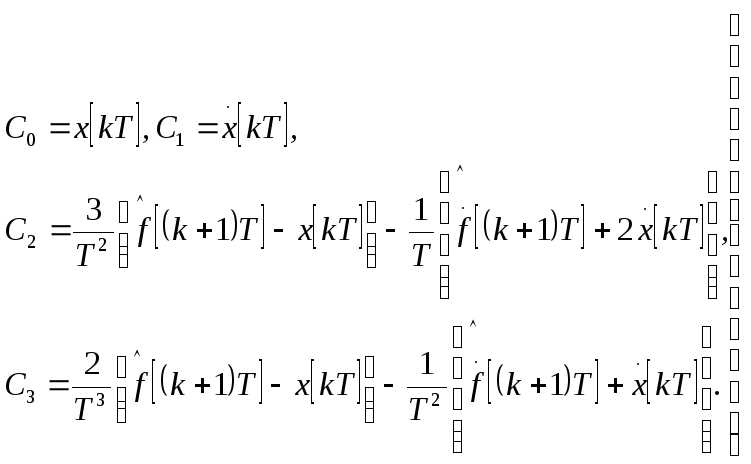(120)

Найдем высшие производные по t выражения (117):

. (121)

Подставляя выражения (117),(118),(121) с коэффициентами (120) в уравнение объекта (116), найдем

.

Здесь управление выражается в явном виде, так как уравнение (116) не содержит производных u(t) .

Данный алгоритм может быть реализован при использовании ЭВМ в контуре управления. При этом U(t) может реализовываться либо с помощью аналогового устройства с переменными коэффициентами, либо с помощью цифрового вычислительного устройства, работающего с периодом дискретности , значительно меньшим Т. Оценки,в простейшем случае могут получаться с помощью конечных разностей решетчатой функции. Следует отметить, что даже при идеальной экстраполяции система будет следить за входным сигналом с ошибкой. Это объясняется тем, что в системе третьего порядка для однозначного задания движения необходимо знать еще и начальную величину ускорения. Здесь же контролируются только координата и ее первая производная. Процесс (117) возможен при условии

.

В противном случае реальный процесс x(t) отличается от определяемого по формуле (117) и в точку (,) система попадет с некоторой сшибкой, к которой еще добавится ошибка экстраполяции. Однако приведенный алгоритм не накапливает ошибки, более того, возникшую на каком-либо этапе ошибку он постарается исправить на следующем шаге. При необходимости можно включить в число контролируемых параметров и вторую производную.