3. Способ последовательного программирования.

При использовании способа последовательного программирования уравнению системы в операторной форме придается вид

,

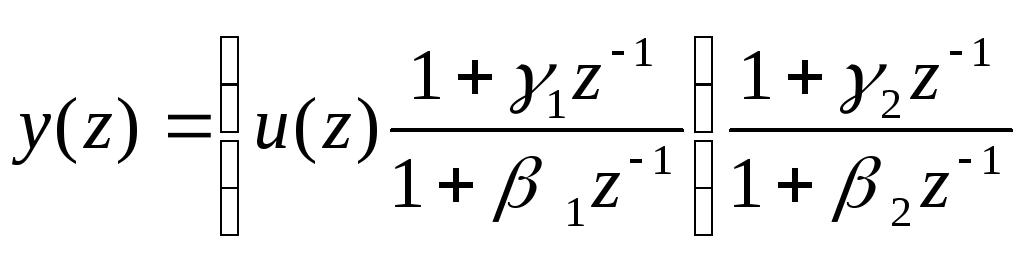полученный разложением на множители числителя и знаменателя передаточной функции (60). Схема моделирования в этом случае строится в виде последовательности однотипных каскадов (рис.З7)

Р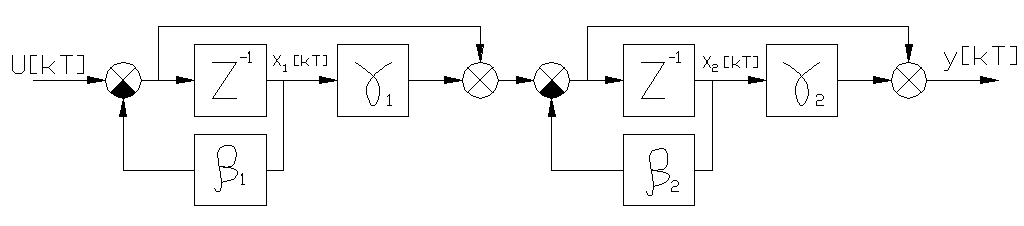ис.37

Уравнения состояния системы имеют вид

а матрицы Ф, Н, C, D определяются выражением

Матрица Ф при этом оказывается треугольной.

Составление блок-схем моделирования дискретных систем является важным этапом их исследования. С помощью этих схем можно рационально выбрать переменные состояния системы, а также перейти к описанию в рамках дискретного преобразования Лапласа или Z-преобразования.

Лекция № 14

Тема:

Анализ дискретных систем с использованием пространства состояний.

План лекции:

1. Вычисление Z–передаточной функции системы.

2. Вычисление Z– передаточной функции дискретной системы управления электродвигателем.

1. ВычислениеZ–передаточной функции системы.

Рассмотрим выполнение обратного перехода от уравнений состояния к передаточным функциям системы. Пусть уравнения состояния дискретной системы имеют вид

(63)

(64)

где вектор переменных состояния,вектор входных воздействий,вектор выходных переменных.

С другой стороны, система может быть описана матричной Z -передаточной функцией, устанавливающей связь между входными и выходными переменными. Найдем Z -передаточную функцию.

Введем Z -преобразования:

Применяя Z -преобразование к обеим частям уравнений (63),(64), найдем

;

откуда получим

и тогда

При нахождении передаточных функций полагаем начальные условия нулевыми, x[0]0. С учетом этого имеем

(65)

Из уравнения (65) получим выражение для матричной передаточной функции дискретной системы в виде

Матричная передаточная функция имеет размерность (*m), элементпредставляет собой передаточную функцию, связывающую j вход и i выход.

Раскрывая выражение для матричной передаточной функции, получим

где - присоединенная матрица (напомним, что это транспонированная матрица алгебраических дополнений элементов исходной матрицы).

Из последней зависимости видно, что полюсы передаточной функции W(z) являются корнями уравнения

определяющего характеристические числа матрицы Ф. Таким образом, матричная Z-передаточная функция W(z) имеет своими полюсами характеристические числа матрицы Ф.

Алгоритмы получения передаточных функций, основанные на использовании уравнений состояния, удобнее алгоритмов, построенных на формулах -преобразования. Использование ЭВМ в задачах исследования дискретных систем позволяет применять стандартные программы обращения матриц, что приводит к существенному снижению трудоемкости выполняемых вычислений.

2. ВычислениеZ– передаточной функции дискретной системы управления электродвигателем.

Рассмотрим получение уравнений состояния и вычисление передаточной функции для электродвигателя постоянного тока с независимым возбуждением. Уравнения непрерывной части (объекта управления) имеют вид

где - угол поворота выходного вала двигателя;- частота вращения выходного вала двигателя; u - управляющее якорное напряжение; k - коэффициент передачи двигателя по напряжению; T- электромеханическая постоянная времени двигателя.

Возмущающими воздействиями, действующими на объект управления, пренебрежем. Будем считать, что управление u(t) остается постоянным на интервале квантования

Выберем вектор состояния и запишем уравнения объекта в матричной форме:

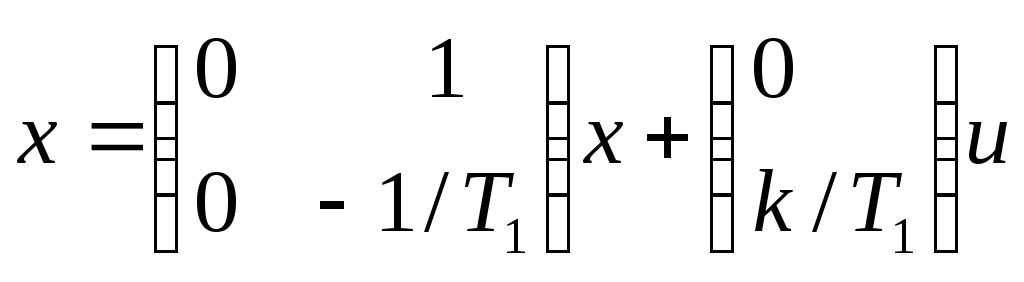
Для вычисления собственной матрицы системы разностных уравнений Ф воспользуемся формулой

где

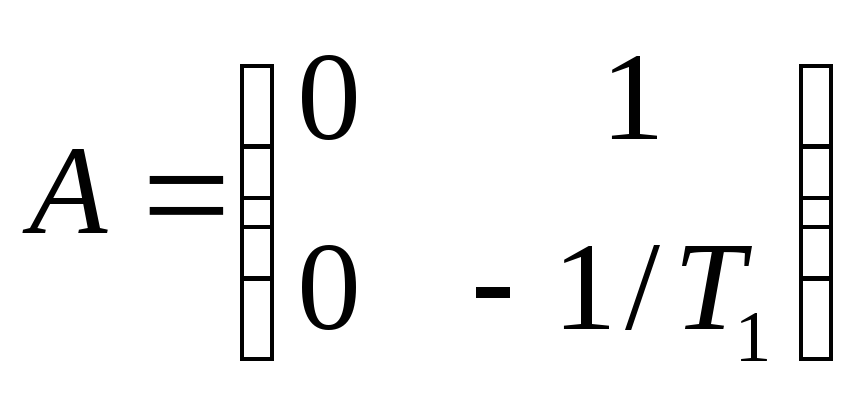
Вычислим обратную матрицу

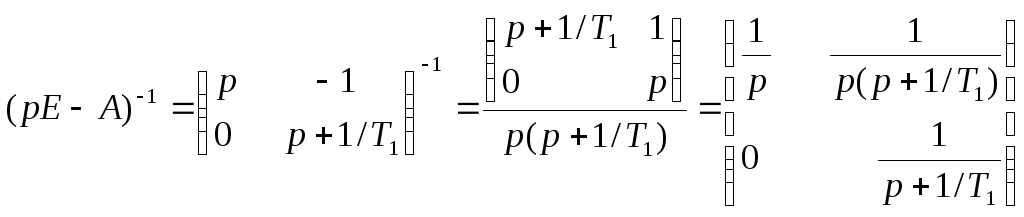
и найдем обратное преобразование Лапласа

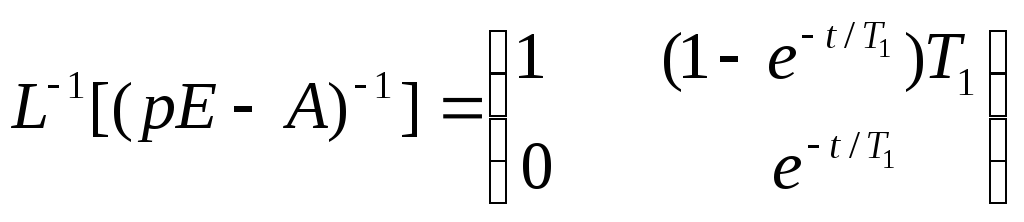
Подставив в последнее равенство t=T , получим собственную матрицу система разностных уравнений:

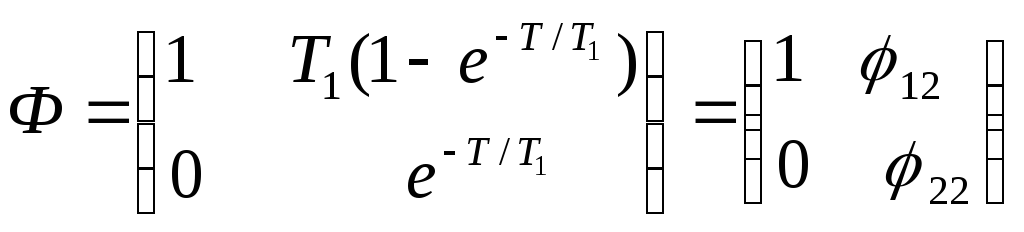
где

Для определения элементов матрицы Н найдем решение дифференциальных уравнений объекта при нулевых начальных условиях и u=1

Подставив в полученные зависимости t=T , найдем матрицу H :

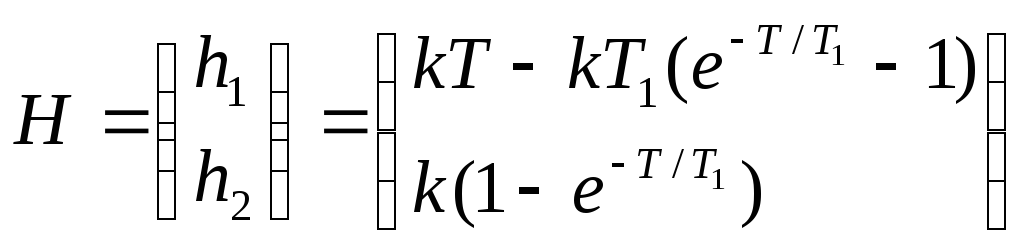
Система разностных уравнений, описывающая поведение объекта при выбранных переменных состояния, будет иметь вид

Примем за выходную переменную угол поворота вала двигателя, т.е. . При этом матрицы С и D преобразуются к виду

C=(1,0) ; D=(0)

Тогда выражение для z-передаточной функции будет следующим:

Раскрывая выражения для матриц С, Ф, Н и произведя преобразования, получим