Лекция № 13

Тема:

Выбор переменных состояния дискретной системы.

План лекции:

1. Способ прямого программирования.

2. Способ параллельного программирования.

3. Способ последовательного программирования.

1. Способ прямого программирования.

Рассмотрим переход от описания импульсной системы с помощью Z-передаточных функций к описанию с помощью переменных состояния. Как уже отмечалось, выбор переменных состояния не является единственным, и определяется выбором соответствующего базиса. Практически удобным приемом выбора переменных состояния является составление схем моделирования дискретных систем. Схемы включают в себя элементы задержки на такт и сумматоры. Пpи выбope пepeмeнныx cocтoяния импульсных систем за них удобно принимать выходы элементов задержки на такт.

Рассмотрим три способа перехода от Z-передаточной функции дискретной системы к уравнениям (57), (58): способы прямого программирования, последовательного программирования и параллельного программирования на примере звена второго порядка с одним входом и одним выходом и передаточной функцией

При способе прямого программирования, разделив числитель и знаменатель передаточной функции на (в общем случае на), получим

(60)

По определению передаточной функции

Введем новую переменную e[kT], Z-преобразование которой имеет вид

.

Тогда

или

В соответствии с выражением (60) составляем схему моделирования (рис.35). При этом учитываем, что множитель соответствует задержке переменной на один такт квантования.

Р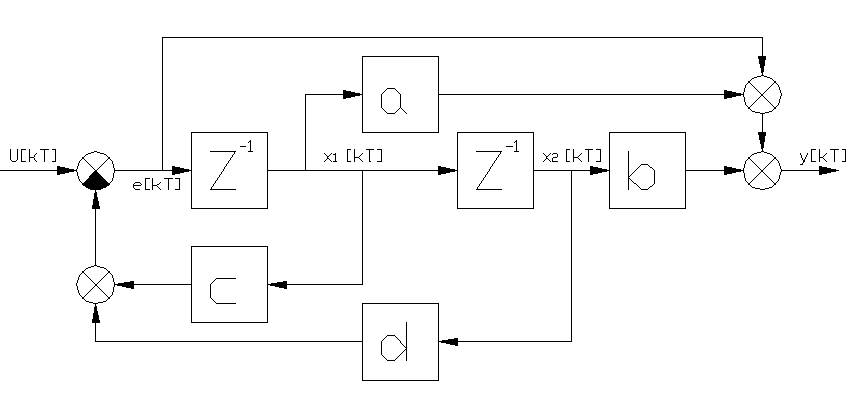ис. 35

Уравнения состояния системы можно получить, записывая соотношения, связывающие координаты на выходах элементов задержки. В итоге имеем

. (61)

Так как

и при этом

,

то для выходной переменной y[kT] получим уравнение

(62)

Таким образом, уравнения (57), (58) принимают вид (61). (62), а матрицы Ф, Н, C, D определяются выражениями

.

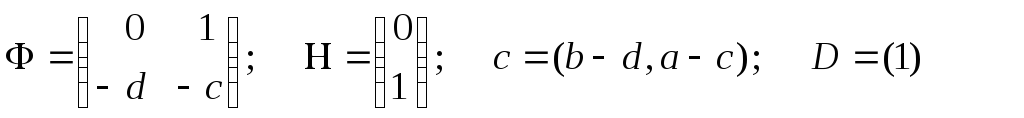Запись системы уравнений (61) для общего случая не представляет сложности. При этом матрица Ф будет иметь структуру, аналогичную собственной матрице системы дифференциальных уравнений, записанных в первой нормальной форме Коши.

2. Способ параллельного программирования.

Рассмотрим способ параллельного программирования. Передаточная функция системы, приведенная к виду (60), разбивается на сумму элементарных звеньев.

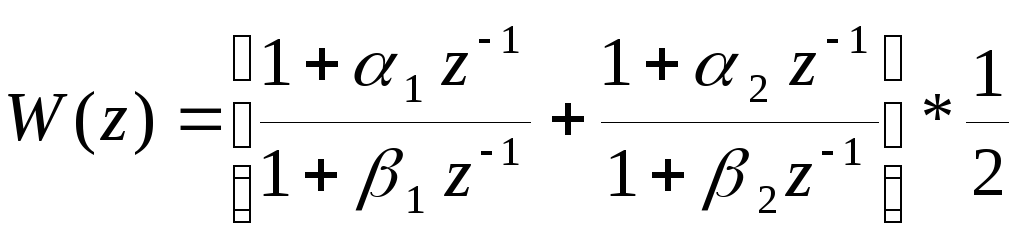
Изображение переменных состояния определяется выражениями

Соответствующая схема моделирования представлена на рис.36.

Р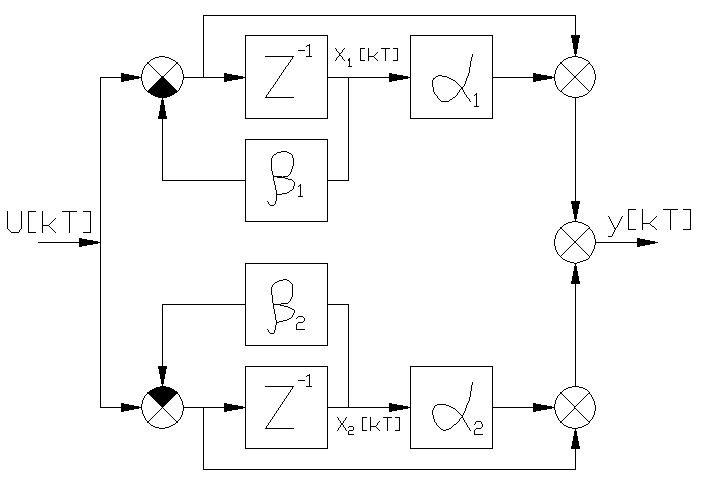ис.36

Разностные уравнения системы имеют вид

Прежде чем записать уравнение для выходной переменной системы, наполним некоторые преобразования передаточной функции

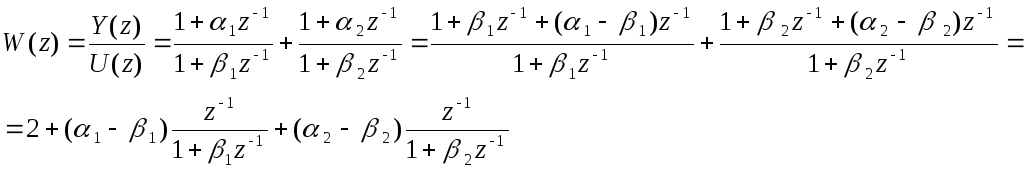
Переходя от изображений к оригиналам, получим

При таком выборе переменных состояния матрицы Ф, Н, С, Dсоответственно имеют вид

Преимущество этого подхода состоит в том, что собственная матрица дискретной системы Ф оказывается .диагональной, но при этом числа (корни характеристического уравнения системы) могут оказаться комплексными. Такие же уравнения можно получить, если передаточную функциюнепосредственно разложить на простейшие дроби и каждой дроби поставить в соответствие переменную состояния.