«Решение задач линейного программирования (лп)»

Методы линейного программирования получили широкое распространение при решении практических задач, связанных с составлением оптимальных производственных планов, графиков обслуживания потребителей, оптимальным распределением ресурсов, транспортных потоков, размещением оборудования, с составлением различного рода смесей и т.д.

Основные сведения

В большинстве оптимизационных задач зависимости между переменными x_iлинейны. Линейность математической модели предполагает наличие у нее свойств пропорциональности и аддитивности.

Свойство пропорциональностьозначает то, что вклад каждой переменной в целевую функцию ЦФ и общий объем потребления соответствующих ресурсов прямо пропорционален уровню (величине) этой переменной.

Аддитивностьзаключается в том, что целевая функция ЦФ представляет собой сумму вкладов от различных переменных. Аналогично левая часть каждого ограничения должна представлять собой сумму расходов, каждое слагаемое которой пропорционально величине соответствующей переменной. Если, например, фирма, производит два конкурирующих вида продукции, увеличение сбыта одного из которых отрицательно сказывается на объеме реализации другого, то такая модель не обладает свойством аддитивности.

Математическая модель задачи линейного программирования (ЛП) в достаточно общем случае формулируется следующим образом:

F=c₁x₁+c₂x₂+... + c_nx_n min(илиmax); (F- целевая функция ЦФ)

при следующих ограничениях на вектор искомых переменных x={x_i}:

a₁₁ x₁ + a₁₂ x₂ + ... + a_1n x_n  (=, ) b₁

a₂₁ x₁ + a₂₂ x₂ + ... + a_2n x_n  (=, ) b₂

………………. .

a_m1 x₁ + a_m2 x₂ + ... + a_mn x_n  (=, ) b_m

x_j  0, j=1, 2, ... n

Для решения задач ЛП различных типов с помощью компьютерных средств удобно использовать математический пакет Mathcadи табличный процессорExcel.Ниже рассматриваются примеры решения типовых задач ЛП с применением этих программных средств.

В среде Mathcad решение задачи ЛП находится в рамках так называемых вычислительных блоков (начинаются с ключевого словаGiven) с использованием встроенных функцийMminimizeилиMaximizeдля минимизации или минимизации целевой функции. В прилагаемых примерах приведены решения нескольких типовых задач, в которых показано, что и как должно быть введено для получения решения. Целевую функцию и ограничения можно записывать в виде отдельных выражений, а также и в векторно-матричной форме, которая является лишь более удобной и компактной формой записи условий задачи ЛП.

В пакете Excel задачи ЛП решают с помощью встроенной функции «Поиск решения».

А. Одноиндексные задачи ЛП

Пример А.1. Решение одноиндексной задачи ЛП в Mathcad

Пример А.2. Решение одноиндексной задачи ЛП в Mathcad

Пример А.3. Задача планирования объемов производства

Задача №1. Фирма производит изделия двух видов A1 и A2 с помощью последовательной обработки каждой из них в трех цехах. Исходные данные задачи приведены в таблице:

Названия цехов	Нормы затрат времени на 1 изделие, час/сут		Объем ресурсов, час/сут
	изделие А1	изделие А2
В1	0,1	0,2	12
В2	0,2	0,1	10
В3	0,3	0,3	21
Прибыль на одно изделие, у.е.	65	80

Определить количества x_j, j = 1,2 , изделий Aj , которые необходимо изготовить для достижения максимальной прибыли

F = 65·x₁ + 80·x₂, (3.1)

т.е. найти оптимальный план суточного выпуска изделий А1 и А2. Это типичная задача производственного планирования.

Отметим, что значения x₁и x₂не могут быть выбраны произвольно, так как существуют ограничения на суточное время работы в цехах. Эти ограничения записываются в виде:

0,1·х₁+ 0,2·х₂≤ 12

0,2·х₁+0,1·х₂ ≤10

0,3·х₁+ 0,3·х₂ ≤ 21 (3.2)

Кроме того значения x₁и x₂не могут быть отрицательными:

x₁ ≥ 0; x₂ ≥ 0; (3.3)

Требуется найти такое неотрицательное решение x₁, x₂системы линейных неравенств (3.2), при котором целевая функция (3.1) принимает максимальное значение.

Решение одноиндексной Задачи №1 в системе Mathcad

Целевая функция F:

F(x) := 65x₁ + 80x₂

Описание ограничений в матричном виде:

- матрица Мсодержит коэффициенты при неизвестных в левой части ограничений, а векторv- правые части исходных неравенств:

M:=v:=(3.2)

Решим задачу с помощью вычислительного блока

Given ... Maximize

Для формирования нулевого приближения полагаем значение х₂равным нулю (инициализация решения)

x₂ := 0

Given

M*x ≤ v x ≥ 0

Таким образом, точка максимума целевой функции F имеет координаты x₁ = 20, x₂ = 50, а значение ее значение в точке максимума:

.

Решение одноиндексной Задачи 1 в пакете Excel

Для решения оптимизационных задач в табличном процессоре Excelиспользуется пункт «Поиск решения» (Solver – Решатель) в меню «Сервис» на панели инструментов. Если этого пункта нет, то необходимо установить соответствующую надстройку. Для этого в менюСервиснужно выбрать пунктНадстройкии в диалоговом окне установить флажок слева от надписи «Поиск решения». В меню «Сервис» появится пункт «Поиск решения».

Решение.В соответствии сисходнымиданнымиЗадачи 1составим и заполним вExcel следующую таблицу

Числа в ячейках столбца «Ограничения»подсчитаны с помощью формул. Формула=СУММПРОИЗВ(В3:С3;$B$7:$C$7)-D3введена в ячейкуF3и продолжена в ячейкиF4:F5таблицы.

Эта формула также скопирована в F6, но без вычитаемогоD6. Выделим ячейкуF6 с целевой функцией и вызовем Решатель «Сервис/ Поиск решения». В диалоговом окне укажем: «Установить целевую ячейку:»$F$6, «максимальное значение», «Изменяя ячейки:»$B$7:$C$7, «Ограничения:»$F$3:$F$5 <= 0.

Так как все ограничения имеют одинаковые знаки «<=», тоздесьони введены блоком. Заметим, что количества x_j , j = 1, 2 изделий являютсяцелымичислами. Поэтому необходимо наложить еще одно ограничение:$B$7:$C$7=целое(целочисленная оптимизация).

В окне «Параметры» установим флажки «Линейная модель» и «Неотрицательные значения». Запустим «Выполнить».

Поиск решениявернет результат: х₁= 20; х₂= 50. Целевая функция равна Fmax = 5300. Этот результат поиска максимума функции F совпадает с результатами, полученными ранее с помощью пакета Mathcad.

Пример А.4. Задача о сплавах

Задача №2. Для изготовления сплава из меди, олова и цинка в качестве сырья используют два сплава тех же металлов, отличающихся составом и стоимостью. Данные об этих сплавах приведены в таблице:

Компоненты сплава	Содержание компонентов в сплаве №i, %
	Сплав № 1	Cплав № 2
Медь	10	10
Олово	10	30
Цинк	80	60
Стоимость1 кг, у.е.	5	4

Полученный сплав должен содержать не более 2 кг меди, не менее 3 кг олова, а содержание цинка может составлять от 7,2 до 12,8 кг.

Определить количества x_j, j = 1, 2 сплавов каждого вида, обеспечивающие получение нового сплава с минимальными затратами на сырье.

Эта задача математически формулируется следующим образом.

Требуется найти минимумцелевой функции

F = 5·x₁+ 4·x₂, (6.1)

при следующих ограничениях:

0,1x₁+ 0,1x₂≤2,

0,1x₁+ 0,3x₂≥3,

0,8x₁+ 0,6x₂≥7,2 (6.2)

0,8x₁+ 0,6x₂≤12,8

x₁,x₂≥0

Эти неравенства описывают ограничения, накладываемые на количество того или иного металла в полученном сплаве.

Решение Задачи №2 в Mathcad

Целевая функция:

F(x):= 5x₁+4x₂

Предварительно поменяв знаки второго и третьегонеравенств (6.2) на противоположные, опишем ограничения с помощью матрицМиv:

M:=v:=

Решим задачу с помощью вычислительного блока Given...minimize.

Инициализация решения:

x₂:= 0

Given

M* x ≤ v x ≥ 0

Minimize(F, x)=

Т.е, точка минимума целевой функции F имеет координаты x₁ = 2, x₂= 9.333333

Значение функции F в точке минимума:

Решение Задачи №2 в среде EXCEL

В соответствии с данными Задачи 2составим и заполним в Excel следующую таблицу:

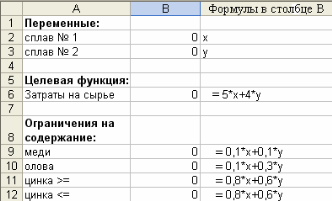
В этой таблице ячейкам В2иВ3присвоены имена х и у соответственно с помощью команд «Вставка/ Имя► Присвоить…».

В ячейки В2иВ3занесены нулевые значения. В ячейкиВ6,В9-В12введены формулы, указанные в таблице 8.1 справа от соответствующих ячеек.

Выделим ячейку B6 с формулой для целевой функцией и вызовем Решатель «Сервис/ Поиск решения». В диалоговом окне укажем: «Установить целевую ячейку:»$B$6, «минимальное значение», «Изменяя ячейки:»$B$2:$B$3, «Ограничения:»$B$9 <= 2;$B$10 >=3;$B$11 >=7,2;$B$12 <=12,8(рис. 8.1).

Рис. 8.1

В окне «Параметры» установим флажки «Линейная модель» и «Неотрицательные значения». Запустим «Выполнить». Поиск решения вернет результат: х = 2; y = 9,333333333. Целевая функция равна Fmin = 47,33333333. Этот результат поискаминимумафункции F совпадает с результатами, полученными ранее в системеMathcad.

Б. Пример двухиндексной задачи ЛП (о загрузке оборудования).

Задача 3 Имеются три землеройные машины вида М1, М2, М3. Нужно выполнить три вида землеройных работ (А, В, С) в количестве: А – 6000 м³; В – 5000 м³; С –8000 м³. Все необходимые данные приведены в следующей таблице:

Машины	Производит. Pijм3/ч			Стоимость 1 часа Cij, грн./ч			Ресурсы времени Ti, ч.
	A	B	C	A	B	C
М1	30	20	40	2	4	3	200
М2	20	30	50	3	2	2	150
М3	40	40	20	5	3	6	150
Объем работ Vi, м3/	6000	5000	8000

Нужно найти оптимальный план загрузкимашин, обеспечивающий минимальные суммарные денежные затраты на выполнения всего объема работ при заданном ресурсе времени.

Решение

Построение математической модели задачи.

Обозначим через X_ij– время работыi– ой машины наj– ом виде работ (i=1, 2, 3;j= 1, 2, 3).

Целевая функцияZ(ЦФ) выражает затраты денежных средств на выполнение работ:

Z = 2X₁₁ + 4X₁₂ + 3X₁₂ + 3X₂₁ + 2X₂₂+ 2X₂₃ +5X₃₁ + 3X₃₂ + 6X₃₃  min

или

Здесь C_ij– стоимость 1 часа работыi– ой машины наj– ом виде работ.

Ограничения:

 Объем работ должен быть выполнен

30X₁₁+ 20X₂₁+ 40X₃₁= 6000;

20X₁₂+ 30X₂₂+ 40X₃₂= 5000;

40X₁₃ + 50X₂3 + 20X₃₃ = 8000.

или

Здесь Р_ij– производительностьi– ой машины наj– ом виде работ.

 Ограничения на ресурс времени.

X₁₁+X₁₂+X₁₃150;

X₂₁+X₂₂ +X₂₃200;

X₃₁+X₃₂+X₃₃150.

или

 Неотрицательность плана работ.

X_ij0 (i=1, 2, 3;j= 1, 2, 3)

Решение Задачи 3 в Mathcad