Задача 9
9.1.
Найти проекцию точки Р(6;4;7)
на плоскость
.
9.2.
Найти проекцию точки Р(10;6;7)
на плоскость
.
9.3.
Найти проекцию точки Р(–2;11;7)
на плоскость
.
9.4.
Найти проекцию точки Р(10;7;–7)
на плоскость
.
9.5.
Найти проекцию точки Р(–4;7;5)
на плоскость
.
9.6.
Найти проекцию точки Р(2;–1;3)
на прямую
.
9.7.
Найти проекцию точки Р(5;6;–9)
на прямую
.
9.8.
Найти проекцию точки Р(5;5;–4)
на прямую
.
9.9.
Найти проекцию точки Р(6;–16;5)
на прямую
.
9.10.
Найти проекцию точки Р(3;2;6) на прямую
.
Задача 10
Установить, что каждое из следующих уравнений определяет гиперболу, и найти координаты ее центра С, полуоси, эксцентриситет, уравнения асимптот и уравнения директрис. Изобразить гиперболу на чертеже, указав фокусы, асимптоты и директрисы.
10.1.
10.2.
10.3.
10.4.
10.5.
Установить, что каждое из следующих уравнений определяет эллипс, и найти координаты его центра С, полуоси, эксцентриситет, уравнения директрис. Изобразить эллипс на чертеже, указав оси симметрии, фокусы и директрисы.
10.6.
10.7.
10.8.
10.9.
10.10.
КОНТРОЛЬНАЯ РАБОТА № 2
Введение а анализ
ЗАДАЧА 11
Найти предел, не пользуясь правилом Лопиталя.
11.1.
.11.2.
.11.3.
.
11.4.
.11.5.
.11.6.
.
11.7.
.11.8.
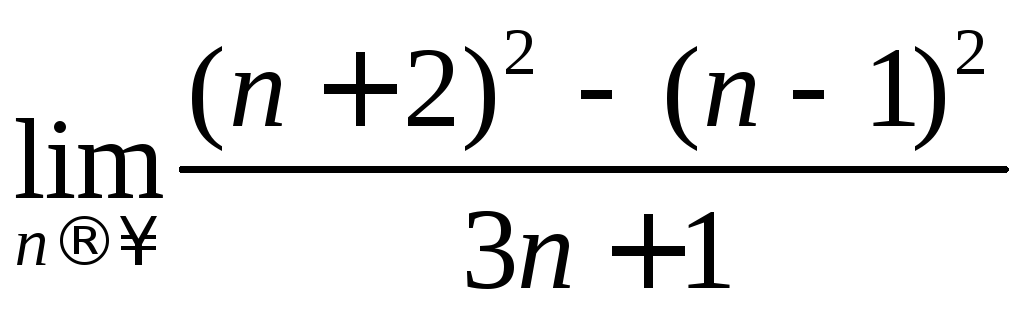.11.9.
.
11.10.
.
ЗАДАЧА 12
Найти предел, не пользуясь правилом Лопиталя.
12.1.
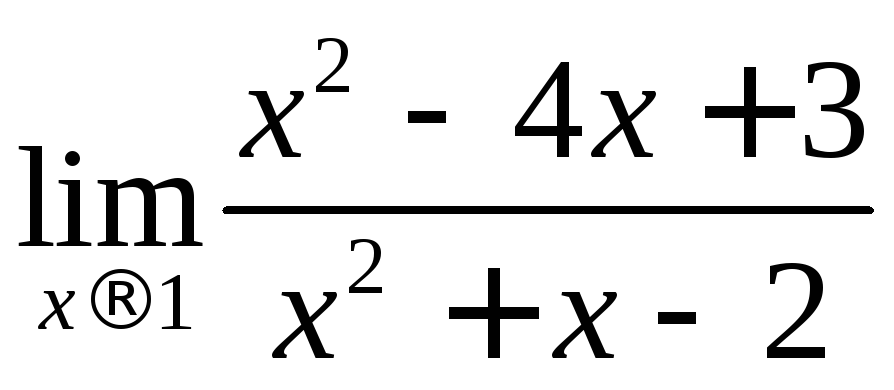.12.2.
.12.3.
.
12.4.
.12.5.
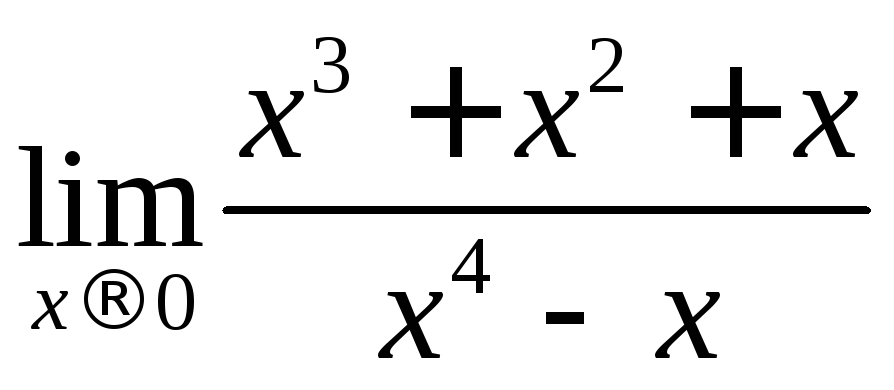.12.6.
.
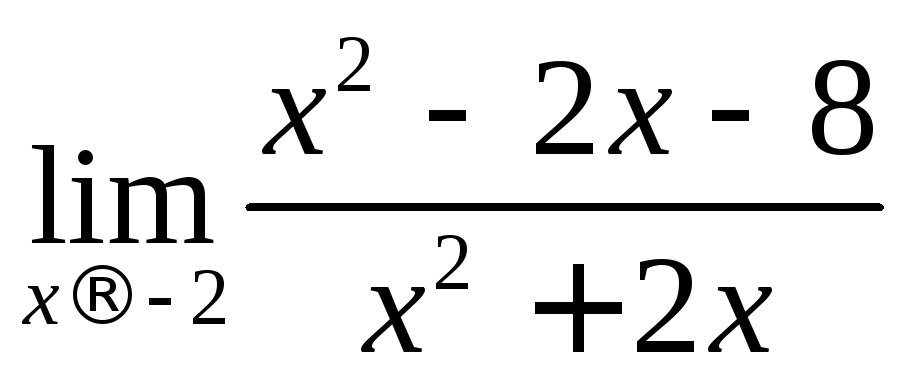12.7.
.12.8.
.12.9.
.
12.10.
.
ЗАДАЧА 13
Найти предел, не пользуясь правилом Лопиталя.
13.1.
.13.2.
.13.3.
.
13.4.
.13.5.
.13.6.
.
13.7.
.13.8.
.13.9.
.13.10.
.
ЗАДАЧА 14
14.1.
.14.2.
.
14.3.
.14.4.
.14.5.
.
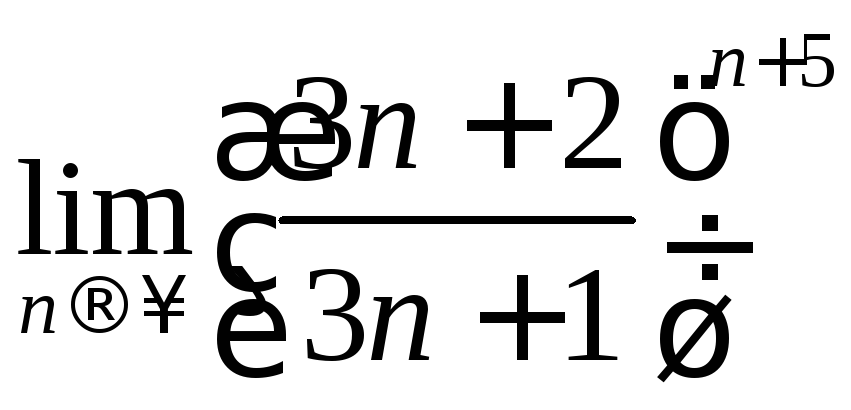14.6.
.14.7.
.14.8.
.
14.9.
.14.10.
.
ЗАДАЧА 15
Найти предел, используя эквивалентность бесконечно малых функций.
15.1.
.15.2.
.15.3.
.
15.4.
.15.5.
.15.6.
.15.7.
.15.8.
.15.9.
.15.10.
.
ЗАДАЧА 16
Задана функция
.
Исследовать точки разрыва функции, если
они существуют. Сделать схематический
чертеж.
16.1.
.16.2.
.16.3.
.16.4.
.
16.5.
.16.6.
.16.7.
.16.8.
.
16.9.
.16.10.
.
ЗАДАЧА 17
17.1.
17.2.
17.3.
17.4.
17.5.
17.6.
71.7.
17.8.
17.9.
17.10.
КОНТРОЛЬНАЯ РАБОТА № 3
Дифференциальное исчисление
ЗАДАЧА 18
Показать, что
функция
удовлетворяет соответствующему
дифференциальному уравнению.
18.1.
.18.2.
.
18.3.
18.4.
18.5.
18.6.
18.7.
18.8.
18.9.
18.10.
ЗАДАЧА 19
Найти производную функции.
19.1.
19.2.
19.3.
19.4.
19.5.
19.6.
.
19.7.
19.8.
19.9.
19.10.
ЗАДАЧА 20
Найти производную от функции, заданной неявно.
20.1.
20.2.
20.3.
20.4.
20.5.
20.6.
20.7.
20.8.
20.9.
20.10.
ЗАДАЧА 21
Найти производную второго порядка от функции, заданной параметрически.
21.1.
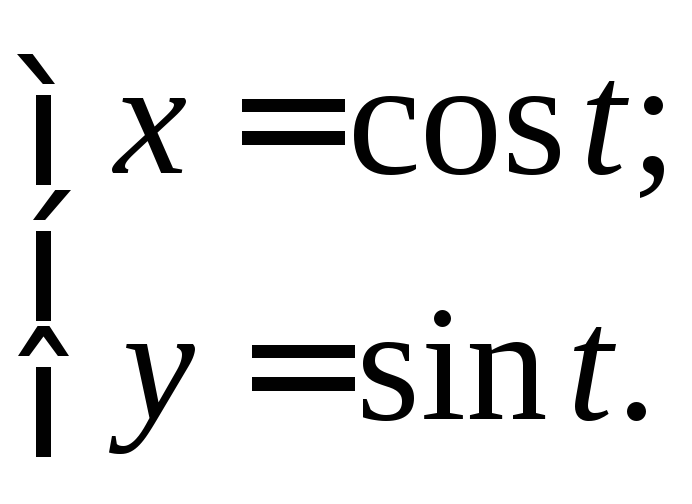21.2.
21.3.
21.4.
21.5.
21.6.
21.7.
21.8.
21.9.
21.10.
ЗАДАЧА 22
Найти уравнения
касательной и нормали к графику функции
в точке
.
22.1.
22.2.
22.3.
22.4.
22.5.
22.6.
22.7.
22.8.
22.9.
22.10.
ЗАДАЧА 23
Найти предел по правилу Лопиталя.
23.1.
23.2.
23.3.
23.4.
23.5.
23.6.
23.7.
23.8.
23.9.
23.10.
ЗАДАЧА 24
Найти наименьшее
и наибольшее значения функции
на отрезке
.
24.1.
24.2.
24.3.
24.4.
24.5.
24.6.
24.7.
24.8.
24.9.
24.10.
ЗАДАЧА 25
Найти интервалы
выпуклости, вогнутости и точки перегиба
графика функции
.
25.1.
.25.2.
.25.3.
.
25.4.
.25.5.
.25.6.
.
25.7.
.25.8.
.25.9.
.25.10.
.
ЗАДАЧА 26
Провести полное
исследование функции
и
построить ее график.
26.1.
26.2.
26.3.
26.4.
26.5.
26.6.
26.7.
26.8.
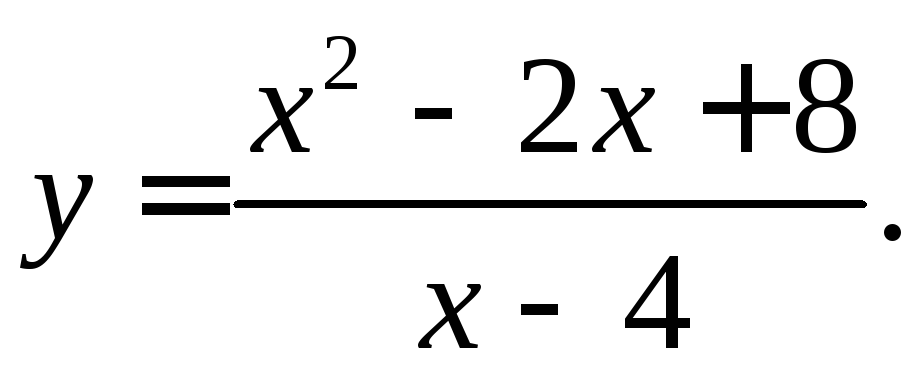
26.9.
26.10.
ЗАДАЧА 27
27.1.
27.2.
27.3.
27.4.
27.5.
27.6.
27.7.
27.8.
27.9.
27.10.
КОНТРОЛЬНАЯ РАБОТА № 4
Интегралы
ЗАДАЧА 28
Найти интеграл.
28.1.
.28.2.
.28.3.
.
28.4.
.28.5.
.28.6.
.
28.7.
.28.8.
.28.9.
.
28.10.
.
ЗАДАЧА 29
Найти интеграл.
29.1.
.29.2.
.29.3.
.29.4.
.
29.5.
.29.6.
.29.7.
.
29.8.
.29.9.
.29.10.
.
ЗАДАЧА 30
Найти интеграл.
30.1.
.30.2.
.30.3.
.
30.4.
.30.5.
.30.6.
.
30.7.
.30.8.
.30.9.
.
30.10.
.
ЗАДАЧА 31
Найти интеграл.
31.1.
.31.2.
.
31.3.
.31.4.
.
31.5.
.31.6.
.31.7.
.
31.8.
.31.9.
.31.10.
.
ЗАДАЧА 32
Вычислить интеграл.
32.1.
.32.2.
.32.3.
.32.4.
.
32.5.
.32.6.
.
32.7.
.32.8.
.
32.9.
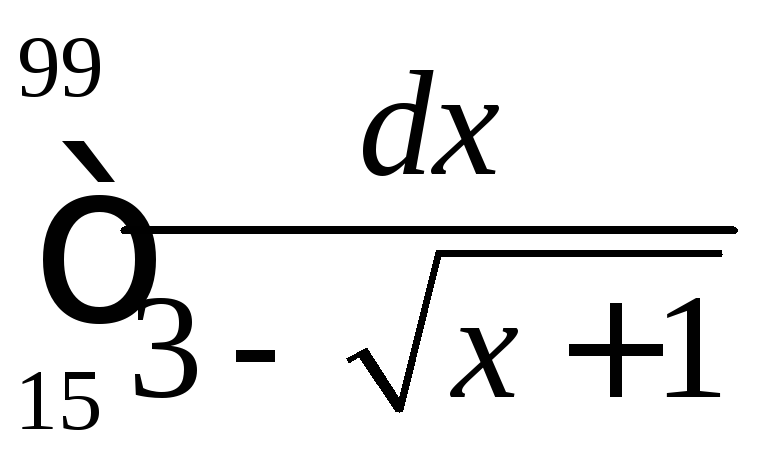.32.10.
.
ЗАДАЧА 33
Вычислить интеграл.
33.1.
.33.2.
.33.3.
.
33.4.
.33.5.
.33.6.
.33.7.
.33.8.
.33.9.
.33.10.
.
ЗАДАЧА 34
Найти площадь фигуры, ограниченной линиями.
34.1.
.34.2.
.34.3.
.
34.4.
.34.5.
.
34.6.
.34.7.
.
34.8.
.34.9.
.34.10.
.
ЗАДАЧА 35
Вычислить несобственные интегралы (или установить их расходимость).
35.1.
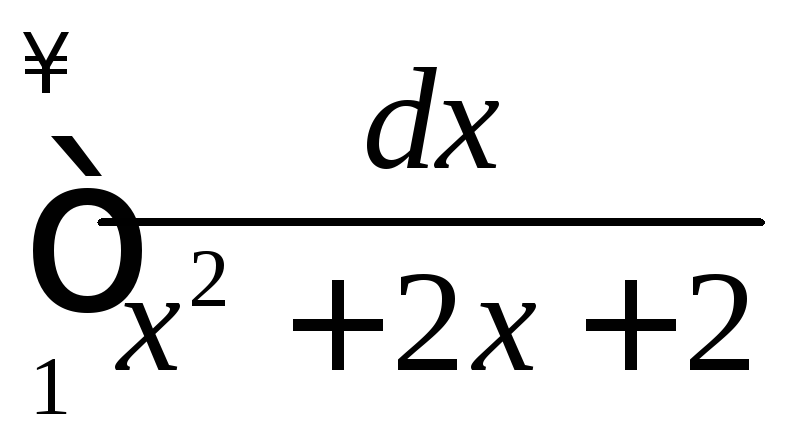.35.2.
.35.3.
.35.4.
.
35.5.
.35.6.
.35.7.
.35.8.
.35.9.
.35.10.
.