
Контрольная работа
.pdf
11
Прибыль от реализации одной единицы товара первого вида составляет 2 ден. ед., второго вида – 3 ден. ед.
Составьте оптимальный план реализации товаров, обеспечивающий торговому предприятию максимальную прибыль.
Вариант 22
Фабрика выпускает три вида тканей, причем суточное плановое задание составляет: не менее 90 м ткани I вида, 70 м – II вида и 60 м III вида. Суточные ресурсы следующие: 780 единиц производственного оборудования, 850 единиц сырья и 790 единиц электроэнергии, расход которых на 1 м ткани представлен в таблице. Цена 1м ткани I вида равна 80 ден. ед., II вида – 70 ден. ед., III вида – 60 ден. ед. Определите, сколько метров тканей каждого вида следует выпустить, чтобы общая стоимость выпускаемой продукции была максимальной.
Вариант 23
Торговое предприятие реализует товары трех групп: А, В. С. Известны нормативы затрат ресурсов в расчете на единицу товара и ограничения по располагаемым ресурсам даны в таблице. Составьте оптимальный план товарооборота по критерию «максимум дохода».
Вариант 24
Для составления плана выпуска четырех видов продукции P1, P2, P3 и P4 на предприятии используют три вида сырья S1 S2 и S3. Объемы выделенного сырья, нормы расхода сырья и прибыль, полученная в результате выпуска каждого вида продукции, приведены в таблице. Какое количество продукции всех видов необходимо производить, чтобы прибыль была максимальной.
12
Вариант 25
Бройлерное хозяйство птицеводческой фермы насчитывает 20000 цыплят, которые выращиваются до 8-недельного возраста и после соответствующей обработки поступают в продажу. Недельный расход корма в среднем (за 8 недель) составляет 500г=0,5кг.
Для того, чтобы цыплята достигли к 8й неделе необходимого веса, кормовой рацион должен удовлетворять определенным требованиям по питательности. Этим требованиям могут соответствовать смеси различных видов кормов, или ингредиентов.
В таблице приведены данные, характеризующие содержание (по весу) питательных веществ в каждом из ингредиентов. Смесь должна содержать не менее 0,8% калия, не менее 22 белка и не более 5 клетчатки от общего веса смеси. Определите количество (в кг) каждого из 3х ингредиентов, образующих смесь минимальной стоимости, при соблюдении требований к общему расходу кормовой смеси и ее питательности.
Вариант 26
Предприятие выпускает продукцию 4х видов П1П4 с использованием для этого ресурсов, виды и нормы расхода по которым, а так же уровень получаемой от их реализации прибыли приведены в таблице. Составьте вариант оптимального плана производства по критерию максимума прибыли.
Вариант 27
Фабрика «GRM plc» выпускает два вида каш для завтрака – «Crunchy» и «Chewy». Используемые для производства обоих продуктов ингредиенты в основном одинаковы и как, правило, не являются дефицитными. Основным ограничением, накладываемым на объем выпуска, является наличие фонда рабочего времени в каждом из трех цехов фабрики.
Управляющему производством Джою Дисону необходимо разработать план производства на месяц. В приведенной ниже таблице указаны общий фонд рабочего времени и число человеко-часов, требуемое для производства 1 т продукта.
|
Необходимый фонд рабочего |
Общий фонд рабочего |
||
Цех |
времени, чел.-ч/т |
|||
времени, чел.-ч. в месяц |
||||
|
|
|
||
|
|
|
|
|
|
«Crunchy» |
«Chewy» |
|
|
А. Производство |
10 |
4 |
1000 |
|
В. Добавка приправ |
3 |
2 |
360 |
|
С. Упаковка |
2 |
5 |
600 |
|
13
Доход от производства 1 т «Crunchy» составляет 150 ф. ст., а от производства «Chewy» – 75 ф. ст. На настоящий момент нет никаких ограничений на возможные объемы продаж. Имеется возможность продать всю произведенную продукцию.
Вариант 28
Предприятие производит для автомобилей ВАЗ запасные части типа А и В. Норма расхода ресурсов для производства каждого вида запасных частей, а также отведенные лимиты ресурсов приведены в таблице.
|
Норма расхода ресурсов на |
Лимит ресурсов (в |
|
Ресурсы |
производство 1 детали |
неделю) |
|
|
Тип А |
Тип В |
|
Трудозатраты, чел.-час. |
4 |
3 |
8000 |
Листовой материал, кг |
2 |
6 |
7500 |
Полимерный материал, |
5 |
2 |
6000 |
кг |
|
|
|
Доход от продажи 1 |
11 |
13 |
|
детали |
|
|
|
Производственная мощность позволяет выпускать максимум 3500 деталей типа А. Общее число производимых деталей в течение одной недели должно составлять не менее
1500 штук.
Определите, сколько деталей каждого вида следует производить, чтобы обеспечить максимальный доход от продажи за неделю.
14
Задание № 2. Графический метод решения задачи линейного программирования
ЗАДАНИЕ:
Найти графическим методом решение следующей задачи линейного программирования.
Вариант |
Задача |
|
|
|
|
|
Z=2x1+3x2 max, |
|
|
x1+2x2 4, |
|
1 |
2x1-x2 9, |
|
5x1+3x2 30, |
||
|
4x1+7x2 28, |
|
|
x1, x2 0. |
|
|
|
|
|
Z=3x1-3x2 max, |
|
|
x1-4x2 4, |
|
2 |
3x1+2x2 6, |
|
-x1+x2 7, |
||
|
x1+2x2 2, |
|
|
x1, x2 0. |
|
|
|
|
|
Z=3x1+4x2 max, |
|
|
-2x1+x2 1, |
|
|
4x1+6x2 12, |
|
3 |
6x1+3x2 9, |
|
|
x1+x2 6, |
|
|
2x1-4x2 2, |
|
|
x1, x2 0. |
|
|
|
|
|
Z=x1+2x2 max, |
|
|
x1+x2 4, |
|
|
3x1+x2 4, |
|
4 |
x1+5x2 4, |
|
x1 3, |
||
|
||
|
x2 3, |
|
|
x1, x2 0. |
|
|
|
|
|
Z=x1+x2 max, |
|
|
-4x1+x2 1, |
|
|
2x1 - 3x2 6, |
|
5 |
2x1+x2 8, |
|
-x1+x2 7, |
||
|
||
|
x1+2x2 2, |
|
|
x1, x2 0. |
|
|
|
|
15 |
|
|
|
|
|
Z=2x1+x2 max, |
|
|
2x1 - x2 4, |
|
6 |
3x1+2x2 3, |
|
3x1 - x2 6, |
||
|
7x1+x2 7, |
|
|
x1, x2 0. |
|
|
|
|
|
Z=x1+x2 max, |
|
|
-4x1 +x2 2, |
|
7 |
2x1 - 3x2 3, |
|
2x1 +x2 8, |
||
|
x1 - 4x2 4, |
|
|
x1, x2 0. |
|
|
|
|
|
Z=7x1+6x2 max, |
|
|
2x1 +5x2 10, |
|
8 |
5x1+2x2 10, |
|
x1 6, |
||
|
x2 5, |
|
|
x1, x2 0. |
|
|
|
|
|
Z=x1+5x2 min, |
|
|
x1 - 2x2 2, |
|
9 |
-2x1 - 3x2 -4, |
|
|
-2x1 +x2 2, |
|
|
x1, x2 0. |
|
|
|
|
|
Z=3x1+x2 max, |
|
|
-x1 +x2 1, |
|
10 |
x1 +3x2 15, |
|
|
-2x1 +x2 4, |
|
|
x1, x2 0. |
|
|
|
|
|
Z=3x1+2x2 max, |
|
|
x1 - 2x2 ≤ 1, |
|
11 |
-2x1 - 3x2 -2, |
|
-2x1 +x2 4, |
||
|
||
|
x1, x2 0. |
|
|
|
|
|
Z=3x1+2x2 min, |
|
|
x1 - 2x2 ≤ 1, |
|
12 |
-2x1 - 3x2 -2, |
|
-2x1 +x2 4, |
||
|
||
|
x1, x2 0. |
|
|
|
16
Z=3x1+4x2 max,
x1 + 2x2 ≤ 4, -2x1 - 2x2 ≥ 2,
13 2x1 +4x2 ≥ 8, x1 + 2x2 ≤ 6,
4x1 - 2x2 ≤ 4, x1, x2 0.
Z=5x1+x2 min,
x1 + 7x2 ≥ 7, 5x1 +2x2 ≥ 10,
-2x1 +x2 6,
14 7x1 + x2 ≥ 7,
2x1 +5x2 ≥ 10,
2x1 12, x2 7, x1, x2 0.
Z=-6x1+8x2 min, 9x1 + 3x2 ≥ 9,
15 -2x1 +2x2 4,
2x1 - 3x2 ≤ -5, x1, x2 0.
Z=5x1 - 3x2 min, 3x1 + 2x2 ≥ 6,
2x1 - 3x2 ≥ -6,
16 x1 – x2 4,
4x1 + 7x2 ≤ 14, x1, x2 0.
Z=5x1+3x2 min, 2x1 + 2x2 ≥ 6,
2x1 – 2x2 ≥ -6,
17 x1 +2x2 4,
4x1 +3 x2 ≤ 12, x1, x2 0.
Z=2x1- 3x2 min,
3x1 + 2x2 ≥ 6,
18 x1 – 0,5x2 ≤ 2, x1 +2,5x2 5,
x1, x2 0.
Z=2x1 – 4x2 max, 8x1 – 5x2 ≤ 16,
19 x1 +3x2 ≥ 3,
2x1 + 5x2 ≤ 10, x1, x2 0.
|
|
17 |
|
|
|
||
|
Z=x1+3x2 max, |
||
|
-3x1 + 4x2 ≤ 12, |
||
20 |
3x1 |
+ 3x2 ≤ 9, |
|
3x1 |
- 4x2 ≤ 3, |
||
|
|||
|
2x1 |
+ 3x2 ≤ 6, |
|
|
x1, x2 0. |
||
|
|
||
|
Z=2x1+3x2 max, |
||
|
2x1 |
– 4x2 8, |
|
23 |
x1 + x2 4, |
||
|
3x1 |
+ 6x2 ≤ 12, |
|
|
x1, x2 0. |
||
|
|
||
|
Z=4x1+2x2 min, |
||
|
x1 + 4x2 8, |
||
24 |
5x1 |
+ 3x2 15, |
|
7x1 |
+ x2 7, |
||
|
3x1 |
+ 5x2 15, |
|
|
x1, x2 0. |
||
|
|
||
|
Z=2x1 – 4x2 min, |
||
|
4x1 |
+ 3x2 ≤ 12, |
|
25 |
x1 + 3x2 6, |
||
2x1 |
+ 5x2 10, |
||
|
|||
|
x1, x2 0. |
||
|
|
||
|
Z=x1+4x2 max, |
||
|
-x1 + x2 ≤ 5, |
||
26 |
x1 + x2 ≤ 8, |
||
3x1 |
+2 x2 ≤ 18, |
||
|
|||
|
x1, x2 0. |
||
|
|
||
|
Z=2x1+x2 max, |
||
|
-x1 +2x2 14, |
||
|
7x1+4x2 28, |
||
27 |
4x1 |
- 3x2 12, |
|
|
5x1+2x2 10, |
||
|
10x1 - 8x2 2, |
||
|
x1, x2 0. |
||
|
|
||
|
Z=x1 +2x2 min, |
||
|
-3x1 + 4x2 ≤ 12, |
||
28 |
x1 + 4x2 4, |
||
3x1 |
- 4x2 10, |
||
|
|||
|
x1, x2 0. |
||
|
|
|
|
18
Методические указания к выполнению контрольной работы
1. Общая характеристика задачи линейного программирования
Математическое программирование («планирование») – это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ограничения. Методы математического программирования используются в экономических, организационных, военных и др. системах для решения так называемых распределительных задач.
Распределительные задачи возникают в случае, когда имеющихся в наличии ресурсов не хватает для выполнения каждой из намеченных работ эффективным образом и необходимо наилучшим образом распределить ресурсы по работам в соответствии с выбранным критерием оптимальности.
Линейное программирование является наиболее простым и лучше всего изученным разделом математического программирования. Характерные черты задач линейного программирования следующие:
1)показатель оптимальности L(X) представляет собой линейную функцию от элементов решения X x1, x2,..., xn ;
2)ограничительные условия, налагаемые на возможные решения, имеют вид линейных равенств или неравенств.
Общая форма записи модели задачи линейного программирования:
Целевая функция
L X c1x1 c2 x2 ... cn xn max min ,
при ограничениях
a11x1 |
a12 x2 |
... a1n xn |
( , )b1 , |
||||||||||
|
|
|
|
a22 x2 |
|
... a2n xn |
( , )b2 , |
||||||
a21x1 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
... |
|
|
|
(1.1) |
|
|
|
|
|
|
|
|
|
|
|
|
||
a |
m1 |
x |
a |
m2 |
x |
2 |
... a |
mn |
x |
n |
( , )b , |
||
|
|
1 |
|
|
|
|
m |
||||||
x , x |
,...x |
k |
0 k n . |
|
|
|
|||||||
|
1 |
2 |
|
|
|
|
|
|
|
|
|
||
При описании реальной ситуации с помощью линейной модели следует проверять наличие у модели таких свойств, как пропорциональность и аддитивность.
Пропорциональность означает, что вклад каждой переменной в целевой функции и общий объем потребления соответствующих ресурсов должен быть прямо пропорционален величине этой переменной. Например, если, продавая j-й товар в общем случае по цене 100 рублей, фирма будет делать скидку при определенном уровне закупки до уровня цены 95 рублей, то будет отсутствовать прямая пропорциональность между доходом фирмы и величиной переменной x j . Т.е. в разных ситуациях одна единица j-го товара будет
приносить разный доход.
Аддитивность означает, что целевая функция и ограничения должны представлять собой сумму вкладов от различных переменных. Примером нарушения аддитивности служит ситуация, когда увеличение сбыта одного из конкурирующих видов продукции, производимых одной фирмой, влияет на объем реализации другого.
Допустимое решение – это совокупность чисел (план) X x1 , x2 ,..., xn , удовлетворяющих ограничениям задачи (1.1).
19
Оптимальное решение – это план, при котором целевая функция принимает свое максимальное (минимальное) значение.
Модели и методы линейного программирования успешно применяются при решении задач в таких сферах, как промышленное производство, военное дело, сельское хозяйство, экономические исследования, транспорт, здравоохранение, психология, социальные науки.
Наибольшее применение для задач линейного программирования получили алгоритмические способы решения соответствующих задач, которые учитывают специфические особенности целевой функции и множества допустимых решений. Из алгоритмических способов следует отметить симплекс-метод для решения задач линейного программирования и метод потенциалов для решения транспортной задачи.
2. Решение задач линейного программирования с использованием Microsoft Excel
Для решения задач линейного программирования в программе Microsoft Excel реализованы приближенные методы их решения с достаточно высокой степенью точности.
Для того чтобы решить задачу линейного программирования в табличном редакторе MS Excel, необходимо выполнить следующие действия:
1)Ввести условие задачи:
a)создать экранную форму для ввода условия задачи:
переменных,
целевой функции,
ограничений,
граничных условий;
b)ввести исходные данные в экранную форму:
коэффициенты целевой функции,
коэффициенты при переменных в ограничениях,
правые части ограничений;
c)ввести зависимости из математической модели в экранную форму:
формулу для расчета целевой функции,
формулы для расчета значений левых частей ограничений;
d)задать целевую функцию (в окне «Поиск решения»):
целевую ячейку,
направление оптимизации целевой функции;
e)ввести ограничения и граничные условия (в окне «Поиск решения»):
ячейки со значениями переменных,
граничные условия для допустимых значений переменных,
соотношения между правыми и левыми частями ограничений.
2)Решить задачу:
a)установить параметры решения задачи (в окне «Поиск решения»);
b)запустить задачу на решение (в окне «Поиск решения»);
c)выбрать формат вывода решения (в окне «Результаты поиска решения»).
Пример. Одноиндексные задачи линейного программирования. Рассмотрим пример нахождения решения для следующей одноиндексной задачи ЛП:
|
|
|
|
20 |
|
|
|
||
L X 130,5x1 20x2 |
56x3 87,8x4 |
max; |
|||||||
1,8x1 2x2 x3 4x4 |
756, |
|
|||||||
6x 2x |
|
4x x 450, |
(2.1) |
||||||
|
|
1 |
2 |
3 |
4 |
|
|||
4x |
1,5x |
10,4x |
13x 89, |
|
|||||
|
|
1 |
2 |
3 |
|
4 |
|
||
|
|
|
|
||||||
x |
|
|
|
|
|
|
|
|
|
j |
0; |
j 1,4. |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
1. Ввод исходных данных.
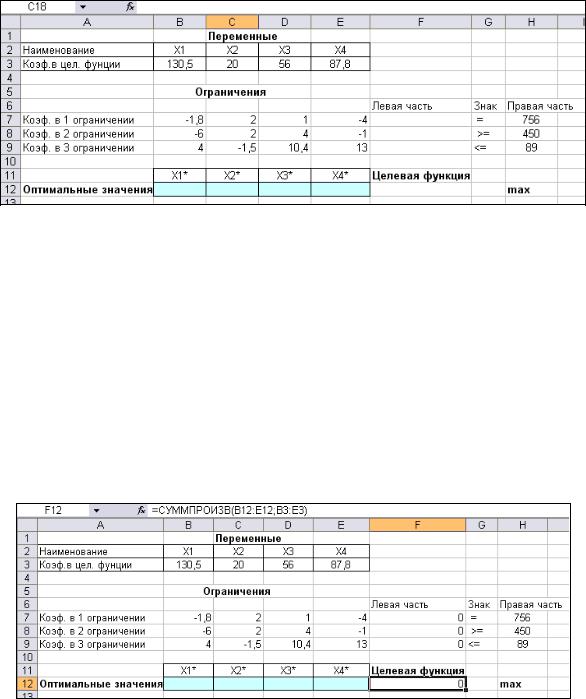
Создание экранной формы и ввод в нее условия задачи. Экранная форма для ввода условий задачи (2.1) вместе с введенными в нее исходными данными представлена на рисунке 2.1.
Рис. 2.1. Экранная форма задачи (2.1)
Ввод зависимостей из математической модели в экранную форму.
Зависимость для целевой функции. В ячейку F12, в которой будет отображаться значение целевой функции, необходимо ввести формулу, по которой это значение будет рассчитано. Согласно (2.1) значение целевой функции определяется выражением
130,5x1 20x2 56x3 87,8x4 . |
(2.2) |
Используя обозначения соответствующих ячеек в Excel (рис.1.1), формулу для расчета целевой функции (2.2) можно записать как сумму произведений каждой из ячеек, отведенных для значений переменных задачи (B12:E12), на соответствующую ячейку, отведенную для коэффициентов целевой функции (B3:E3), то есть
=СУММПРОИЗВ(B12:E12;B3:E3). |
(2.3) |
После этого в целевой ячейке появится 0 (нулевое значение) (рис.2.2).
Рис. 2.2. Экранная форма задачи (2.1) после ввода всех необходимых формул
