
Лаб_работа_4
.pdfЛАБОРАТОРНАЯ РАБОТА 4. ЗАДАЧА О НАЗНАЧЕНИЯХ
Общая постановка задачи: требуется распределить n работ между n рабочими так, чтобы затраты на выполнение работ были минимальными или эффективность использования рабочей силы была максимальной.
Модель задачи в случае минимизации затрат о назначениях выглядит
так:
n n |
|
cij xij min |
|
j 1i 1 |
|
n |
|
xij |
1, j 1,..., n |
i 1 |
(1) |
n |
|
xij |
1,i 1,..., n |
j 1 |
|
xij 0,i 1,..., n, j 1,..., n,
где: сij – затраты на выполнение i-м рабочим j-й работы;
xij – переменная модели: xij=1, если i-й рабочий назначен на работу j, xij=0, если i-й рабочий не назначен на работу j.
В случае максимизации эффективности использования рабочей силы за сij обозначают коэффициент, показывающий эффективность выполнения i-м рабочим j-й работы, и задача решается на максимизацию целевой функции.
Если количество рабочих не равно количеству работ, задача является открытой или несбалансированной и требует приведения к замкнутому виду путем введения недостающих рабочих или работ в необходимом количестве, для которых все сij = 0.
Пример:
Фирма получила заказ на разработку пяти программных продуктов.
Для выполнения заказа решено привлечь пятерых наиболее опытных программистов. Каждый из них должен написать одну программу. В таблице приведены оценки времени в днях, необходимого программистам для выполнения каждой из этих работ:
|
Программа |
Программа |
Программа |
Программа |
Программа |
|
1 |
2 |
3 |
4 |
5 |
Галкин |
46 |
59 |
24 |
62 |
67 |
Палкин |
47 |
56 |
32 |
55 |
70 |
Малкин |
44 |
52 |
19 |
61 |
60 |
|
|
|
|
|
|
Чалкин |
47 |
59 |
17 |
64 |
73 |
Залкин |
43 |
|
65 |
|
20 |
60 |
|
75 |
д |
|
|
|
|
|
|
|
|
Как |
распределить |
работы |
между программистами, |
чтобы общее |
||||
количество человеко-дней, затраченное на выполнение заказа, было минимальным?
Составим модель линейного программирования, отражающую условие:
46x11 59x12 24x13 62x14 67x15 47x21 56x22
32x23 55x24 70x25 44x31 52x32 19x33 61x34
60x35 47x41 59x42 17x43 64x44 73x45
43x51 65x52 20x53 60x54 75x55 min
5
xij 1, j 1,...,5 (2)
i 1 5
xij 1, i 1,...,5
j 1
|
|
1 |
|
xij |
, i 1,...5; j 1,...,5 |
0 |
|
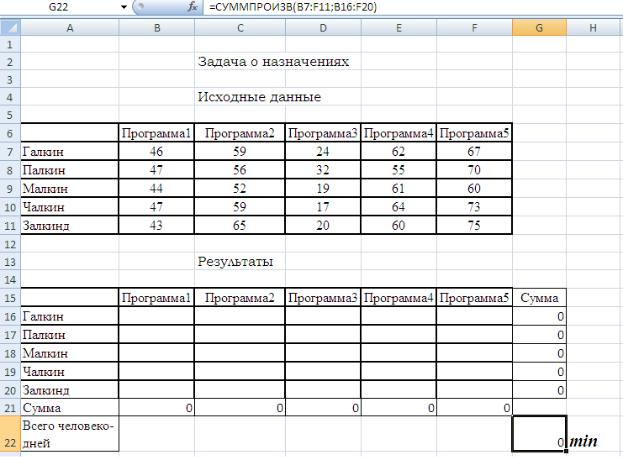
Решим задачу при помощи Microsoft Excel:
Рис. 1
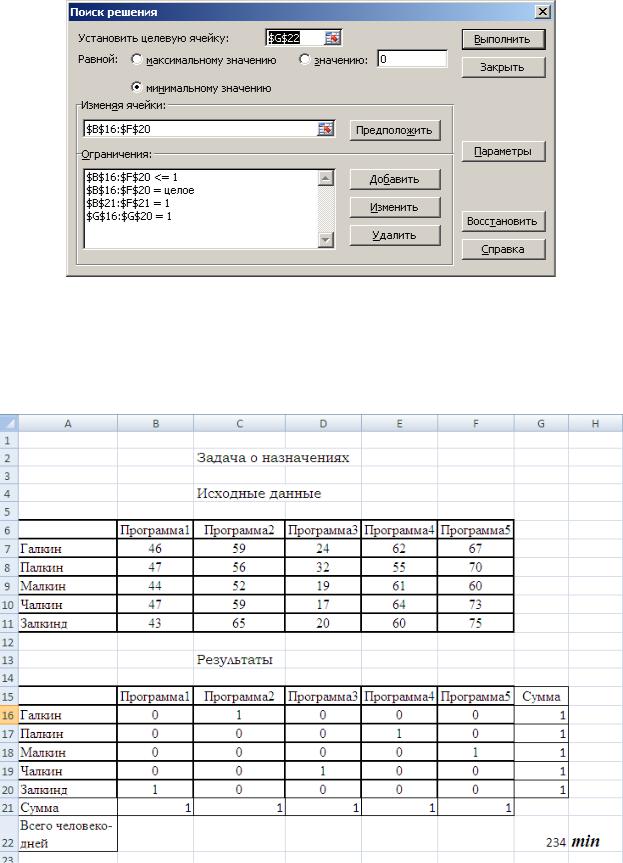
При решении задач о назначении особый интерес вызывает способ ввода ограничений при заполнении формы модуля Поиск решения:
Рис. 2
Проведенные расчеты показывают, что минимальное количество человеко-дней для выполнения заказа составляет 234. Назначение программиста для создания программы определяется наличием на пересечении строки и столбца значения 1.
Рис. 3

Результатом вычислений являются следующие значения переменных:
x12 1 x24 1 x35 1 x43 1
x51 1
Значения остальных переменных равны нулю.
Полученное решение означает, что Галкину будет поручено выполнение программы 2, Палкину – программы 4, Малкину – программы 5, Чалкину – программы 3, Залкинду – программы 1.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Задача 1
В Центральном административном округе города Москвы открываются 4 магазина торговли по предварительным заказам - в районах Басманный, Замоскворечье, Мещанский и Таганский. Идея проекта состоит в том, что товары хранятся на четырех централизованных складах, находящихся в Северном, Северо-Восточном, Южном и Западном административных округах, и несколько раз в день по мере поступления заказов доставляются в магазины небольшими партиями.
Время, затрачиваемое на доставку продукции со складов в магазины, приведено в таблице (в минутах):
|
Басманный |
Замоскворечье |
Мещанский |
Таганский |
Северный |
20 |
30 |
15 |
30 |
Северо-Восточный |
15 |
25 |
20 |
20 |
Южный |
35 |
15 |
30 |
20 |
Западный |
30 |
20 |
20 |
30 |
Руководство сети магазинов должно решить вопрос прикрепления магазинов к складам так, чтобы каждый склад обслуживал только один магазин, а время доставки товаров было минимальным.
Задача 2
Фирма получила заказ на срочный перевод четырех книг с итальянского языка. Фирма может располагать услугами 5 переводчиков, способных выполнить работу такого уровня. Время в днях, за которое каждый переводчик справится с работой, приведено в таблице:
|
Книга 1 |
Книга 2 |
Книга 3 |
Книга 4 |
Иванов |
10 |
25 |
14 |
25 |
Петров |
8 |
12 |
16 |
28 |
Сидоров |
12 |
18 |
17 |
33 |
Андреев |
14 |
23 |
15 |
30 |
Васильев |
11 |
20 |
18 |
28 |

Фирма использует повременную оплату труда. Переводчики имеют разную квалификацию, поэтому за день работы фирма платит Иванову 700 рублей в день, Петрову - 800 рублей в день, Сидорову - 600, Андрееву - 500, Васильеву - 550.
Поскольку по оценке фирмы качество переводов в итоге будет примерно одинаковым, руководство фирмы просит Вас составить такое распределение работ, которое позволит минимизировать затраты на переводы.
Задача 3
Компания "Евростройтур" организует экскурсионные автобусные туры по странам Европы. Компания получила 4 новых автобуса и предполагает направить их на маршруты во Францию, Италию, Чехию и Испанию.
Каждый автобус обслуживают 2 водителя. Компанией приглашены 8 водителей, в различной степени знакомых с дорогами европейских стран (в % от экскурсионного маршрута):
|
Франция |
Италия |
Чехия |
Испания |
Александр |
56 |
43 |
85 |
68 |
Алексей |
56 |
38 |
99 |
70 |
Валентин |
63 |
94 |
54 |
84 |
Василий |
96 |
89 |
65 |
24 |
Николай |
44 |
62 |
63 |
72 |
Виктор |
74 |
85 |
42 |
68 |
Андрей |
23 |
59 |
37 |
92 |
Юрий |
89 |
45 |
53 |
78 |
Необходимо распределить водителей так, чтобы общий показатель освоения маршрутов был максимальным.
