Алгоритм Форда-Фалкерсона:

1. Перенумеровать все вершины сети произвольным образом, кроме истока и стока.

2. Задать некоторый начальный поток в сети (например, нулевой).

3. Вершинам сети присвоить целочисленные метки, а дугам – знаки “+” и “–” по следующим правилам:

а) вершине-истоку присвоить метку ;

б) находим непомеченную вершину , смежную помеченной вершине. Если поток по соединяющей вершиныдуге меньше пропускной способности этой дуги, то происходит помечивание, иначе переходим к рассмотрению следующей вершины. Если вершинаявляется образом помеченной вершины, то происходит прямое помечивание: вершинаполучает метку, равную номеру вершины, соединяющая вершиныдуга получает метку “ + ” и мы переходим к рассмотрению следующей вершины. Если вершина W не имеет ни одного помеченного прообраза, то происходит обратное помечивание: вершинаполучает метку, равную номеру вершины(являющейся в данном случае её образом), соединяющая вершиныдуга получает метку “ – ” и мы переходим к рассмотрению следующей вершины. Процесс помечивания продолжается до тех пор, пока все удовлетворяющие этим условиям вершины не получат метку.

4. Если в результате процедуры помечивания вершина-сток метки не получила, то текущий поток – максимальный, задача решена. В противном случае, перейти к пункту 5.

5. Рассмотреть последовательность вершин , метка каждой из которых равна номеру следующей за ней вершины, и множество дуг, соединяющих соседние вершины из.

Построить новый поток по схеме: если дуга принадлежит множеству и имеет знак “ + ”, то новый поток по этой дуге = старый поток по этой дуге +.

Если дуга принадлежит множеству и имеет знак “–”, то новый поток по этой дуге = старый поток по этой дуге –.

Если дуга не принадлежит множеству , то новый поток по дуге = старый поток по этой дуге.

Схема нахождения К: :

• для нахождения рассматриваются все дуги, принадлежащие множествуи имеющие знак “ + ” и для каждой такой дуги вычисляется разность между пропускной способностью дуги и потоком по этой дуге. Затем из этих значений разностей выбирается минимальное значение и присваивается.

• для нахождения 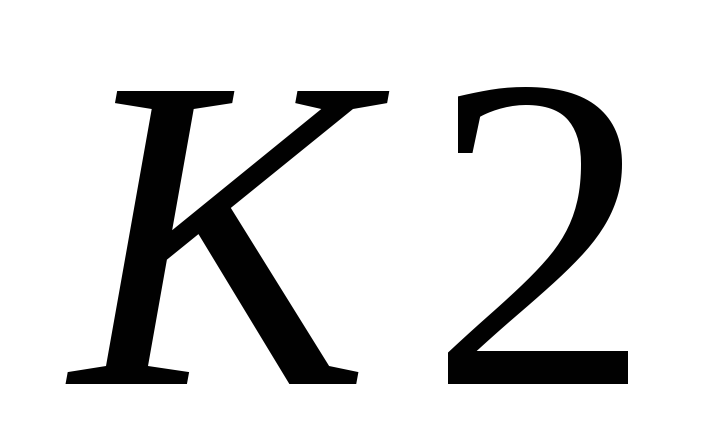рассматриваются все дуги, принадлежащие множествуи имеющие знак “ – ”. Затем из этих дуг выбирается дуга с минимальным потоком и значение потока по этой дуге присваивается.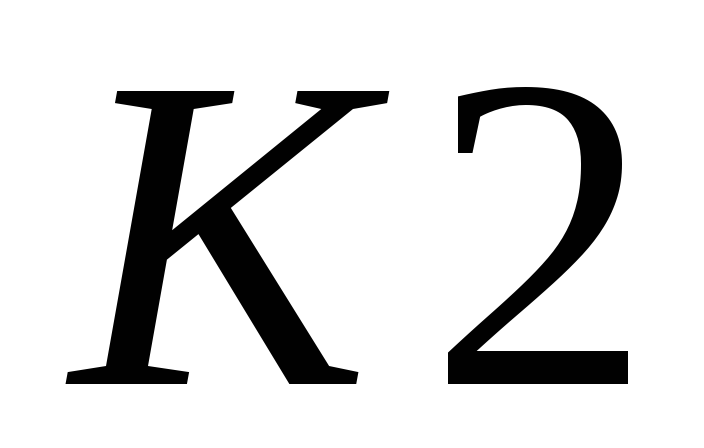

Далее следует перейти к пункту 3.

Алгоритм Форда-Фалкерсона используется при решении многих практических задач. Одна из них – Задача об источниках и потребителях.

Пример. Найти максимальный поток для транспортной сети :

Рисунок 23.11

Пункт 1. Пронумеровать произвольным образом вершины сети:

Рисунок 23.12

Пункт 2. Задать произвольный начальный поток в сети (например нулевой):

Рисунок 23.13

Пункт 3.1. Истоку (вершине №1) присвоить метку «0»

Рисунок 23.14

Пункт 3.2. Прямое помечивание: Пусть – непомеченная, а– помеченная вершины. Тогда вершине, такой чтоприсвоить метку, равную номеру вершины, а дуге– знак «+».

Рисунок 23.15

Обратное помечивание вершине , такой что, присвоить метку равную номеру вершины, а другие– знак «-». Таких вершин на этом шаге не найдено:

Рисунок 23.16

Пункт 4. Вершина №6 (сток) получила метку. Значит, максимальный поток еще не найден. Продолжаем решение.

Рисунок 23.17

Пункт 5. Рассмотрим последовательность вершин , каждая из которых имеет метку, ревную номеру следующей вершины и последовательность дуг, соединяющих соседние вершины из.

Рисунок 23.18

Зададим новый поток по правилу:

Если ;

Если (имеет знак «+»);

Если (имеет знак «-»);

,, имеет знак «+»

,, имеет знак «-»

В нашем случае , новый поток показан на рисунке.

Переход к пункту 3.1:

Пункт 3.1 (вторая итерация). Вершине №1 (истоку) присваиваем метку «0»:

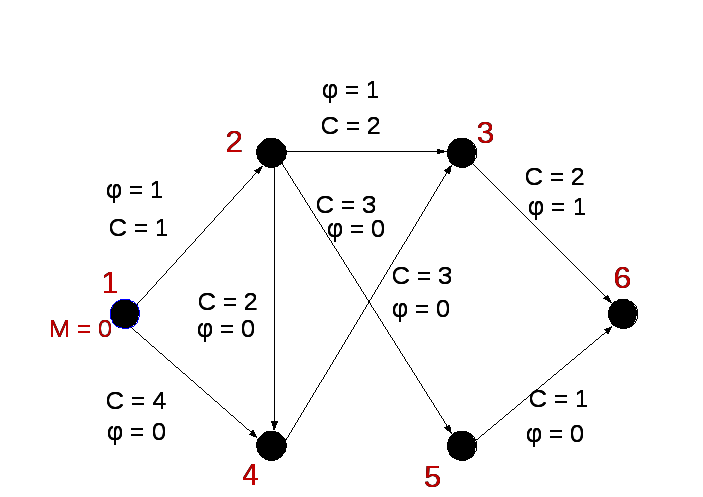
Рисунок 23.19

Пункт 3.2 (вторая итерация). Прямое помечивание:

Рисунок 23.20

Обратное помечивание: соответствующих вершин не найдено.

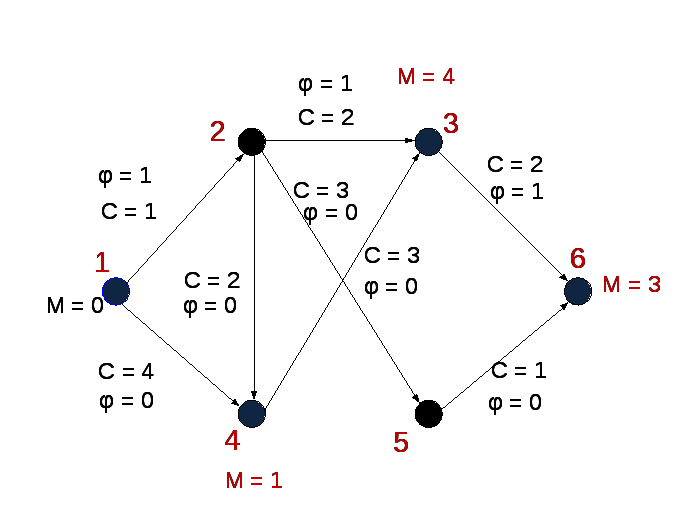
Рисунок 23.21

Пункт 4 (вторая итерация). Вершина №6 (сток) получила метку. Значит, максимальный поток еще не найден. Продолжаем решение:

Рисунок 23.22

Пункт 5 (вторая итерация). ;. Задаем новый поток:

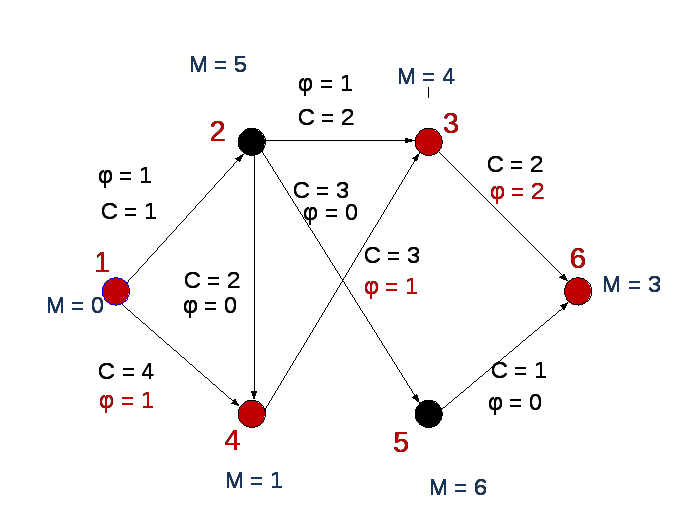
Рисунок 23.23

Пункт 3.1 (третья итерация). Истоку (вершине №1) присвоить метку «0».

Рисунок 23.24

Пункт 3.2 (третья итерация). Прямое и обратное помечивание:

Рисунок 23.25

Пункт 4 (третья итерация). Вершина №6 получила метку. Значит, максимальный поток еще не найден. Продолжаем решение.

Рисунок 23.26

Пункт 5 (третья итерация). ;; Задаем новый поток:

Рисунок 23.27

Пункт 3.1 (четвертая итерация). Исток (вершина №1) получает метку «0».

Рисунок 23.28

Пункт 3.2 (четвертая итерация). Прямое помечивание:

Рисунок 23.29

Обратное помечивание: соответствующих вершин не найдено.

Рисунок 23.30

Пункт 4 (четвертая итерация). Вершин №6 (сток) не получила метку. Значит, задача решена. Максимальный поток найден .

Рисунок 23.40

23.5 Контрольные вопросы и задания

1. Что такое транспортная сеть.

2. Поясните понятие пропускной способности дуг.

3. Приведите и поясните особенности использования алгоритма Дейкстры поиска кратчайших путей.

4. Приведите и поясните особенности использования алгоритма Форда-Фалкерсона.

УЧЕБНО-МЕТОДИЧЕСКИЕ МАТЕРИАЛЫ ПО ДИСЦИПЛИНЕ

Основная литература

1. Бондаренко, М. Ф. Комп’ютерна дискретна математика [Текст] : підручник / М. Ф. Бондаренко, Н. В. Білоус, А. Г. Руткас. – Харків: «Компанія СМІТ», 2004. – 480 с. (існує електронний варіант).

2. Капітонова, Ю. В. Основи дискретної математики [Текст] / Ю. В. Капітонова, С. Л. Кривий, О. А. Летичевський, Г. М. Луцький, М. К. Печорін – Київ: Наукова думка, 2002. – 578 с.

3. Тевяшев, А. Д. Основы дискретной математики в примерах и задачах [Текст] : учеб. пособие для вузов / А. Д. Тевяшев, И. Г. Гусарова. – Харьков: ХНУРЭ, 2003. – 272 с.

4. Бардачев, Ю. Н. Основы дискретной математики [Текст] : учебное пособие / Ю. Н. Бардачев, Н. А. Соколова, В. Е. Ходаков; под редакцией В. Е. Ходакова. – Херсон: ХГТУ, 2000. – 356 с. (існує електронний варіант).

5. Шапорев, С. Д. Дискретная математика. Курс лекций и практических занятий [Текст] / С. Д. Шапорев – СПб.: БХВ-Петербург, 2006. – 400 с. (існує електронний варіант).

6. Кузнецов, О. П. Дискретная математика для инженера [Текст] / О. П. Кузнецов, Г. М. Адельсон-Вельский. – М.: Энергоатомиздат, 1988. – 480 с.

7. Сигорский, В. П. Математический аппарат инженера [Текст] / В. П. Сигорский. – Киев: Техніка, 1977. – 768 с. (існує електронний варіант).

8. Яблонский, С. В. Введение в дискретную математику [Текст] / С. В. Яблонский. – М.: Наука, 1986. – 384 с.

9. Горбатов, В.А. Основы дискретной математики [Текст] / В. А. Горбатов – М.: Высшая школа, 1986. – 312с.

10. Харари, Ф. Теория графов [Текст] / Ф. Харари. – М.: Мир, 1973. – 304 с.

11. Глускин, Л.М. Задачи и алгоритмы комбинаторики и теории графов [Текст] / Л. М. Глускин, В. Я. Шварц, Л. А. Шор. – Донецк: Изд-во ДПИ, 1982. – 110с.

12. Білоус, Н.В. Основи комбінаторного аналізу. [Текст] : навч. посібник / Н. В. Білоус, З. В. Дудар, Н. С. Лєсна, І. Ю. Шубін. – Харків: ХТУРЕ, 1999. – 96 с.

13. Бондаренко, М. Ф. Збірник тестових завдань з дискретної математики [Текст] / М. Ф. Бондаренко, Н. В. Білоус, І. Ю. Шубін. – Харків: ХТУРЕ, 2000. – 156 с. (існує електронний варіант).

Дополнительная литература

14. Новиков, Ф. А. Дискретная математика для программистов [Текст] / Ф. А. Новиков. – СПб: Питер, 2001. – 304 с. (існує електронний варіант).

15. Донской, В.И. Дискретная математика [Текст] / В. И. Донской. – Симферополь: СОНАТ, 2000. – 360 с.

16. Андерсон, Дж. А. Дискретная математика и комбинаторика [Текст] / Джеймс А. Андерсон. – М.: Издательский дом «Вильямс», 2003. – 960 с.

17. Виленкин, Н.Я. Комбинаторика [Текст] / Н. Я. Виленкин. – М.: Наука, 1969. – 328 с.

18. Белоус, Н.В. Тесты. Физика. Математическая логика [Текст] : Навч. посібник / Н. В. Белоус, Е. Е. Гетьманова, З. В. Дударь, В. Ф. Захарченко, М. А. Красноголовец, Н. С. Лесная, В. В. Семенец, В. А. Стороженко, А. А. Харьковская. – Харків: ХТУРЕ, 1998. – 152 с.

19. Капитонова, Ю. В. Лекции по дискретной математике [Текст] / Ю. В. Капитонова, С. Л. Кривой, А. А. Летичевский, Г. М. Луцкий. – СПб.: БХВ-Петербург, 2004. – 624 с.

Методические указания

20. Методичні вказівки до практичних робіт з дисципліни «Дискретна математика» (Частина 1) для студентів усіх форм навчання напряму 6.050101 – комп’ютерні науки / Упоряд. Н. В. Васильцова, Л.Е. Чала – Харків: ХНУРЕ, 2012. – 68 с.

21. Методичні вказівки до самостійної роботи з дисципліни «Дискретна математика» для студентів усіх форм навчання напряму 6.050101 – комп’ютерні науки / Упоряд. Н. В. Васильцова, Л.Е. Чала – Харків: ХНУРЕ, 2014. (навчальне електронне видання).

Глоссарий терминов дисциплины