МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

ХАРЬКОВСКИЙ НАЦИОНАЛЬНЫЙ

УНИВЕРСИТЕТ РАДИОЭЛЕКТРОНИКИ

Конспект лекций по дисциплине «дискретная математика»

для студентов всех форм обучения

направления 6.050101 – «Компьютерные науки»

Электронное издание

УтвержДено

кафедрой «ИУС»

Протокол № 1 от 29.08.2013 г.

кафедрой «ИИ»

Протокол № 1 от 31.08.2013 г.

Харьков 2013

Конспект лекций по дисциплине «Дискретная математика» для студентов всех форм обучения направления 6.050101 – «Компьютерные науки» [Электронное издание] / Состав. Н.В. Васильцова, Л.Э. Чалая. – Харьков: ХНУРЭ, 2013. – 293 с.

Составители Н.В. Васильцова

Л.Э. Чалая

СОДЕРЖАНИЕ

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ 1

ХАРЬКОВСКИЙ НАЦИОНАЛЬНЫЙ 1

УНИВЕРСИТЕТ РАДИОЭЛЕКТРОНИКИ 1

СОДЕРЖАНИЕ 3

Лекция 1. Основы теории множеств. Основные понятия и обозначения теории множеств 10

1.1 Интуитивное понятие множества 10

1.2 Элементы множества 10

1.3 Конечные, бесконечные, счетные множества 12

1.4 Пустое и универсальное множества 13

1.5 Мощность множества 14

1.6 Способы задания множеств 14

1.7 Множество и подмножество 18

1.8. Контрольные вопросы и задания 19

Лекция 2 Алгебра множеств 20

2.1 Геометрическая интерпретация множеств. Круги Эйлера и диаграммы Венна 20

2.2 Операции на множествах 22

2.3 Общее определение алгебры 25

2.4 Понятие алгебры множеств. Аксиомы алгебры множеств 26

2.5 Принцип двойственности 28

2.6 Тождественные преобразования формул алгебры множеств 28

2.7 Контрольные вопросы и задания 29

Лекция 3 Отношения и их свойства. Отношения и операции над ними. 29

3.1 Декартово произведение множеств 30

3.2 Понятие отношений. Бинарные и n-арные отношения 31

3.3 Область определения и область значений отношений 32

3.4 Способы задания отношений 33

3.5 Операции над отношениями 37

3.6 Контрольные вопросы и задания 39

Лекция 4 Свойства бинарных отношений 40

4.1 Основные свойства бинарных отношений 40

4.2 Классы бинарных отношений 42

4.3 Контрольные вопросы и задания 48

Лекция 5 Функциональные отношения. Элементы реляционной алгебры 48

5.1 Функциональные отношения 49

5.2 Элементы реляционной алгебры 52

5.3 Контрольные вопросы и задания 60

Лекция 6. Двузначная логика. Булевы функции. Основные понятия 60

6.1 Двузначная логика 60

6.2 Булевы переменные и функции 61

6.3 Область определения и область значений булевой функции 62

6.4 Способы задания булевых функций 64

6.5 Реализация булевых функций формулами 68

6.6 Принцип двойственности 69

6.7 Булевы алгебры. Законы и тождества булевой алгебры 71

6.8 Контрольные вопросы и задания 75

Лекция 7. Нормальные формы булевых функций 76

7.1 Нормальные формы булевых функций, основные понятия 76

7.3 Теоремы о разложениях булевой функции по переменным 81

7.4 Переход от табличного представления функции к алгебраическому представлению функции 83

7.5 Правила преобразования произвольной формулы алгебры логики в нормальную форму с использованием законов булевой алгебры 84

Лекция 8. Минимизация булевых функций 86

8.1 Основные понятия минимизации булевых функций. Критерии минимизации. 86

8.3 Основные методы минимизации булевых функций. Метод минимизирующих карт (диаграммы Карно-Вейча) 90

8.4 Контрольные вопросы и задания 96

Лекция 9. Алгебра Жегалкина и линейные функции. Функциональная полнота наборов булевых функций 96

9.1 Алгебра Жегалкина и линейные функции 96

9.2 Функциональная полнота булевых функций 99

9.3 Контрольные вопросы и задания 106

Лекция 10. Логика высказываний. Алгебра высказываний. 106

10.1 Высказывания (основные понятия) 106

10.3 Алгебра логики и логика высказываний 111

10.4 Интерпретация формул логики высказываний. Правильные рассуждения 112

10.5 Логическая эквивалентность и логическое следствие 114

10.6 Контрольные вопросы и задания 115

Лекция 11. Исчисление высказываний 115

11.1 Основные понятия исчисления высказываний 115

11.2 Аксиомы и полнота исчисления логики высказываний 116

11.3 Выводимость в исчислении высказываний 117

11.4 Непротиворечивость, независимость 119

11.5 Различные аксиоматизации исчисления высказываний 119

11.6 Некоторые приемы доказательств в исчислении высказываний 121

11.7 Контрольные вопросы и задания 121

Лекция 12. Логика предикатов (логика первого порядка). Предикаты. Алгебра предикатов 122

12.1 Основные понятия логики предикатов 122

12.2 Операции логики предикатов. Кванторные операции 124

12.3 Формулы и их интерпретация в логике предикатов 126

12.4 Законы и тождества логики предикатов 128

12.5 Предваренные нормальные формы 130

12.6 Выводимость в логике предикатов 130

12.7 Контрольные вопросы и задания 131

Лекция 13. Исчисление предикатов 131

13.1 Основные понятия исчисления предикатов 131

13.2 Аксиомы исчисления предикатов 132

13.3 Правила вывода в исчислении предикатов 132

13.4 Контрольные вопросы и задания 133

Лекция 14. Общие определения комбинаторики. Основные правила комбинаторики. Модели типовых комбинаторных конфигураций. 133

14.1 Общие определения комбинаторики. Понятие -выборки. Общие задачи комбинаторики 133

14.2 Основные правила комбинаторики 135

14.3 Модели комбинаторных конфигураций 136

14.4 Контрольные вопросы и задания 141

Лекция 15. Принцип включения и исключения 142

15.1 Теорема и формула включений и исключений 142

15.2 Решето Эратосфена 143

15.3 Частный случай теоремы о включениях и исключениях 143

15.3 Контрольные вопросы и задания 144

Лекция 16. Задачи о распределении предметов по урнам (урновые схемы решения комбинаторных задач) 144

16.1 Задачи о размещении предметов 144

16.3 Распределение n одинаковых предметов по k урнам 145

16.4 Распределение разных предметов без учета порядка предметов по урнам 145

16.5 Распределение разных предметов с учетом их порядка в урнах 145

16.6 Распределение разных предметов между одинаковыми урнами при условии, что урны не пусты 146

16.7 Композиции 152

16.8 Комбинаторика разбиений 152

16.9 Контрольные вопросы и задания 153

Лекция 17. Подходы к изучению комбинаторных объектов и чисел 153

17.1 Понятие продуктивной функции 153

17.2 Рекуррентные соотношения в комбинаторике 155

17.3 Контрольные вопросы и задания 157

Лекция 18. Происхождение графов. Определение графов 157

18.1 Разновидности графов. Неориентированный граф. Определения 157

18.2 Ориентированный граф. Определения 159

18.3 Основные термины для ориентированных и неориентированных графов 159

18.4 Способы задания графов 165

18.5 Контрольные вопросы и задания 171

Лекция 19. Операции над графами. Изоморфизм графов. Плоские и планарные графы 172

19.1 Операции над графами 172

19.2 Гомеоморфные графы 178

19.3 Плоские и планарные графы 178

9.4 Контрольные вопросы и задания 184

Лекция 20. Связность графов. Эйлеровы и гамильтоновы графы 185

20.1 Связность графов, компонента связности. n-связный граф 185

20.2 Свойства связных графов 186

20.3 Компоненты сильной связности ориентированного графа 187

20.4 Алгоритм выделения компонент сильной связности 187

20.5 Метрические характеристики связных графов 190

20.6 Эйлеровы графы 193

20.7 Алгоритм нахождения эйлерова цикла (алгоритм Флери) 195

20.8 Гамильтоновы графы 195

20.9 Алгоритм Робертса-Флореса (метод перебора Робертса-Флореса) нахождения гамильтоновых циклов в графе 196

20.10 Признаки существования гамильтоновых циклов, путей и контуров 199

20. 11 Контрольные вопросы и задания 200

Лекция 21 Деревья 201

21.1 Определение и свойства деревьев 201

21.2 Свойства деревьев 202

21.3 Перечисление графов 202

21.4 Перечисление деревьев 203

21.5 Остовы графа 205

21.6 Алгоритмы построения остовов графа 206

21.7 Ориентированные и бинарные деревья. Определения 209

21.8 Правила прохождения бинарных деревьев 211

21.9 Эквивалентные бинарные деревья 212

21.10 Контрольные вопросы и задания 212

Лекция 22. Цикломатика графов. Раскраска графов 213

22.1 Цикломатика графов 213

22.2 Раскраска графов 219

22.3 Контрольные вопросы и задания 225

Лекция 23. Транспортные сети и потоки. Их свойства 226

23.1 Кратчайшие расстояния и пути в графах 226

23.2 Алгоритм Дейкстры поиска кратчайших путей 226

23.3 Алгоритмы поиска кратчайших путей между всеми парами вершин графа 231

23.4 Транспортные сети и потоки 234

УЧЕБНО-МЕТОДИЧЕСКИЕ МАТЕРИАЛЫ ПО ДИСЦИПЛИНЕ 245

Основная литература 245

Дополнительная литература 246

Глоссарий терминов дисциплины 247

Лекция 1. Основы теории множеств. Основные понятия и обозначения теории множеств

1.1 Интуитивное понятие множества

Понятие множества является одним из наиболее общих математических понятий и как любое другое исходное понятие математической теории оно не определяется точно. Поэтому вместо строгого определения понятия «множество» обычно принимается некоторое основное положение о множестве и его элементах, дается описательное определение, содержание и смысл которого раскрываются при изучении теории множеств. Рассматривая основное положение о множестве и его элементах, чаще всего пользуются определением, предложенным основателем теории множеств немецким математиком Георгом Кантором, который определил множество как «объединение в одно целое объектов, хорошо различимых нашей интуицией и мыслью».

Математическое понятие «множество» связано с абстракцией. Сущность этой абстракции множества заключается в том, что действительно существующие связи объединяемых объектов между собой и с другими объектами игнорируются, а вместо них объединяемым объектам приписываются новые связи друг с другом, выражающие их принадлежность множеству. При этом считается, что два объекта, ничем не отличающиеся друг от друга, являются одним и тем же объектом.

1.2 Элементы множества

Определение. Рассмотрим множество как совокупность объектов произвольной природы, которые удовлетворяют двум свойствам:

• все объекты этой совокупности попарно различимы;

• существует некий признак принадлежности объекта этой совокупности.

Определение. Объекты, которые образуют множество, называются элементами (членами) этого множества.

Пример.

–множество натуральных чисел с нулем;

–множество натуральных чисел;

–множество всех действительных чисел;

–множество всех решений уравнения , то есть;

A  множество прямых, проходящих через заданную точку.

Пример. В качестве признака принадлежности объекта некоторой совокупности (множеству) могут быть следующие свойства (признаки): «быть цифрой», «быть буквой», «быть числом», «быть словом», «быть служебным символом», «быть идентификатором данного», «быть кодом операции» и т.п.

Для обозначения конкретных множеств в общем виде используются различные заглавные буквы или заглавные буквы с индексами, например,. Для обозначения элементов множеств в общем виде используются различные строчные буквыили строчные буквы с индексами.

Утверждение, что множество состоит из различных элементов(и только из этих элементов), условно записывается, т.е. множество обозначается скобками {…}, внутри которых либо просто перечисляются элементы, либо описываются их свойства.

Пример. ;.

Элементами множеств могут быть другие множества, тогда эти элементы обозначаются заглавными буквами.

Пример. , где , , .

. Множество состоит из трех элементов: .

Определение. Множество, элементами которого являются множества, обычно называются классом или семейством.

Семейства множеств обычно обозначают прописными «рукописными» буквами латинского алфавита, чтобы отличить их от множеств, не содержащих множеств в качестве элементов.

Если есть один из объектов множества , то говорим, что есть элемент , или принадлежит . Принадлежность элемента множеству записывается как . Если не является элементом , это записывается как. Символ называется символом принадлежности.

Пример. , но.

Поскольку множество однозначно определяется только элементами, которые оно содержит, порядок перечисления элементов между фигурными скобками произвольный, т.е. , но многократная запись одного и того же элемента – не желательна, т. е..

Определение. При многократной записи одного и того же элемента множество называют мультимножеством и применяют особые методы анализа.

С точки зрения теории множеств, множество и его мультимножество – это один и тот же объект, и они могут между собой не различаться. Однако часто, особенно когда речь идет о представлении множества в памяти вычислительной машины, возникает потребность отличать мультимножество от множества.

Определение. Множество, в котором важны не только его элементы, но и порядок их следования во множестве, называется упорядоченным.

Определение. Конечное множество называется упорядоченным, если его элементы пронумерованы.

Упорядоченное множество обозначают, как правило, либо круглыми, либо треугольными скобками.

Определение. Кортеж (вектор)  это упорядоченный набор элементов . Элементы, образующие кортеж, называютсякоординатами или компонентами. Координаты нумеруются слева направо.

Определение. Число координат кортежа (вектора) называется длиной или размерностью кортежа (вектора).

Пример.

упорядоченное множество, состоящее из 4-х элементов (кортеж длины 4);

, где

Пример. Пусть  множество географических координат долготы и широты. Если поменять местами долготу и широту, то в результате можно попасть в другую точку света.

1.3 Конечные, бесконечные, счетные множества

Множество может содержать любое число элементов – конечное или бесконечное.

Определение. Если множество содержит конечное число элементов, его называют конечным, в противном случае множество называется бесконечным.

Пример. Множество действительных решений квадратичного неравенства конечно, если , и бесконечно, если .

Примеры конечных множеств:

• множество цифр ;

• множество страниц в книге.

Примеры бесконечных множеств:

• множество натуральных чисел;

• множество окружностей на плоскости.

Определение. Множество называетсясчетным, если его объекты можно пересчитывать (каждому объекту множества присвоить натуральное число, которое было бы номером лишь одного элемента множества).

Пример. Множество цифр счетно и конечно, а множество целых чисел – счетно, но не конечно.

1.4 Пустое и универсальное множества

В теории множеств используются понятия «пустого множества» и «универсального множества».

Определение. Множество, не содержащее ни одного элемента, называется пустым и обозначается специальным символом .

Пример. Пусть – множество действительных решений квадратного уравнения . Множество конечно,Если дискриминант отрицателен, множество пусто.

Пример. Множество выигрышей в следующем тираже спортлото на купленные билеты может оказаться пустым.

Пример. Неизвестно, является ли пустым или нет множество всех решений в целых числах уравнения .

Пустое множество введено в математике для удобства и единообразия языка. Роль пустого множества аналогична роли числа нуль. Если исследуется множество объектов, обладающих каким-либо свойством, и впоследствии выясняется, что таких объектов не существует, то гораздо удобнее сказать, что исследуемое множество пусто, чем объявлять его несуществующим. Понятие пустого множества может быть использовано для определения заведомо несуществующей совокупности элементов. Пустое множество будем условно относить к конечным счетным множествам.

Пример. Множество действительных корней уравнения является пустым множеством.

Введем понятие универсального множества.

Определение. Универсальное множество (или универсум), которое обозначают символом , есть множество, содержащее все элементы, принимающие участие в решении определенного класса задач.

Обычно уже в самом определении конкретного множества явно или неявно ограничивается совокупность допустимых объектов, однако данную совокупность удобнее зафиксировать явным образом, определив её в качестве универсума в рамках решаемой задачи.

Примеры. Так, множество слонов следует искать среди млекопитающихся, а не среди рыб.

Если речь идет о множестве чисел, делящихся на 3, то ясно, что оно является множеством целых чисел.

В теории чисел универсум обычно совпадает с множеством всех целых или натуральных чисел.

В математическом анализе универсум может быть множеством всех действительных чисел или множеством всех точек -мерного пространства.

Универсумом зоологии является мир животных; универсумом лингвистики – слова и т.д.

1.5 Мощность множества

При сравнении множеств по числу содержащихся в них элементов возникает понятие мощности множества.

Определение. Мощность конечного счётного множества есть число его элементов, которое обозначают как.

Пример. Мощность множества цифр десятичной системы счисления равна 10.

Мощность множества строчных букв латинского алфавита – 26.

Мощность пустого множества равна нулю (), а мощность множества равна 1, т.е. .

Определение. Если , то множестваиназываютсяравномощными.

1.6 Способы задания множеств

Чтобы задать множество, нужно указать, какие элементы ему принадлежат.

Существует несколько основных способов задания (описания) множеств:

• словесное (вербальное) описание элементов множеств и их основных характеристик;

• простое перечисление элементов множества;

• описание множества с использованием схемы свертывания (указанием характерных свойств элементов множества или характеристической функции множества, заданием порождающей процедуры).

Рассмотрим каждый из перечисленных способов.

Словесное (вербальное) описание элементов множеств и их характеристик используется чаще всего для пояснения и осуществления доказательств основных положений данной теории при решении конкретных задач (применяется в разговорной речи, оформлении различного рода научной и технической документации и т.п.).

Пример. Спецификация задает множество деталей изделия.

Каталог – множество книг в библиотеке.

Простое перечисление элементов множества (неупорядоченного) между фигурными скобками используется, в основном, для описания конечных множеств.

Пример.

есть множество, содержащее натуральные числа 1, 2, 3 и 4.

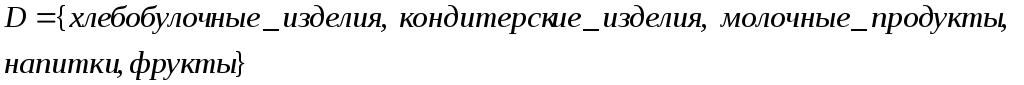есть множество продуктов питания.

Множество гласных букв можно представить как .

–множество решений уравнения .

–множество остатков при делении целых чисел на 7.

Иногда перечислением элементов задают и бесконечное множество. Это делают в тех случаях, когда ясен алгоритм последовательного порождения элементов.

Пример. Множество положительных целых чисел можно обозначить как .

Множество первых n положительных целых чисел обозначается , где точками показано продолжение перечисления элементов.

описывает множество квадратов всех положительных чисел, которые меньше или равны .

описывает множество кубов всех положительных чисел.

Очевидно, что перечисление элементов удобно (целесообразно) только в том случае, когда множество элементов имеет их ограниченное количество или произвольный элемент характеризуется свойством, которое легко описать.

Если же множество имеет, хотя и конечное, однако, большое количество элементов, такое задание множества достаточно громоздко, а в случае бесконечного множества его применение вообще невозможно.

Пример. Используя способы перечисления не так легко описать, например, множество граждан Украины и совершенно немыслимо описать множество действительных чисел.

В общем случае множества можно задавать (описывать) по так называемой схеме свертывания. Схема свертывания может быть реализована при помощи:

• указания характерных свойств элементов множества или характеристической функции множества (характеристическим предикатом);

• заданием порождающей процедуры.

При заданном характеристическом (определяющем) свойстве и заданном классе элементов (универсальном множестве для решаемой задачи) множество определяется как множество, которое содержит все элементы из , обладающие свойством. Для определения по схеме свертывания используется следующая запись.

Пример. Множество четных чисел можно определить какили как, где через обозначено множество целых чисел.

– множество граждан Украины.

–множество слонов.

Свойства, которыми должны обладать элементы формируемого множества , можно описать характеристической функцией (характеристическим предикатом) . Обычно – это высказывание, в котором что-то утверждается об , или некоторая функция переменной.Тогда множество можно представить как . Если класс указан явно, то в этом случае используется запись . Если при замене навысказывание становится истинным или функция в заданной области определения удовлетворяется, то есть элемент данного множества. Таким образом, если истинно.

Пример.

а) – множество чисел, квадрат которых равен двум;

б) – множество чисел, квадрат которых плюс единица больше нуля.

Множество может быть также задано при помощи порождающей процедуры (рекурсивно) .

Определение.

Порождающая процедура – это процедура, которая, будучи запущенной, порождает некоторые объекты, являющиеся элементами определенного множества.

Пример. Множество нечетных чисел можно задать порождающей процедурой .

Множество можно задать рекурсивной процедурой .

При задании множеств могут возникать ошибки и противоречия, поэтому к описанию свойств множеств и их элементов естественно предъявлять требование точности и недвусмысленности. Множество задано корректно, если для любого элемента можно определить, принадлежит он множеству или нет.

Пример. Определение множества как множества, содержащего любые пять натуральных чисел, не является корректным, поскольку невозможно определить точно элементы.

Множество всех простых чисел определено корректно. Для любого натурального числа можно проверить, является ли оно простым, хотя практически на это может потребоваться очень много времени.

Пример. Множество всех хороших фильмов 2011 года разные люди зададут разными списками (может быть пустыми). Сами критерии, по которым производится отбор, при этом будут различны. Такое множество нельзя считать строго заданным.

Неограниченное применение схемы свертывания, некорректность задания множества, свободное использование понятий интуитивного теоретико-множественного универсума иногда ведет к противоречиям, которые называются логическими парадоксами (парадокс Рассела, парадокс Кантора, парадокс Банаха-Тарского) и изучаются в математической логике.

Пример.

Можно получить «множество всех множеств» .Если считать множеством, то получаем .

1.7 Множество и подмножество

Определение. Множество , все элементы которого принадлежат и множеству, называетсяподмножеством (частью) множества . При этом говорят, чтосодержит или покрывает.

Это отношение между множествами называют включением и обозначают символом , т.е. (включено в) или(включает).

Если не является подмножеством, это записывается как. Таким образом,, если существует элемент, не принадлежащий.

Пример:

а) множество конденсаторов электронной цепи является подмножеством всех её компонентов;

б) множество положительных чисел – это подмножество множества действительных чисел.

в) ;

г) .

Пример. Книга из множества книг в шкафу может рассматриваться как множество страниц. Следует обратить внимание на то, что речь идет об элементах множества, а не о подмножествах, т.к. никакая совокупность страниц не может рассматриваться как подмножество множества книг.

Множества иравны, если их элементы совпадают. Иначе говоря,тогда и только тогда, когдаи.

Пример. Если есть множество, аесть множество, тогдаи– равные множества.

Определение.

Если и, точасто называетсясобственным, строгим или истинным подмножеством .Записывается данное отношение как , гдезнак строгого включения.

Пример. Пусть ;, тогда ясно, чтои– собственное (истинное) подмножество.

В частности, каждое множество есть подмножество самого себя. Принято также считать, что пустое множество является подмножеством любого множества. Поэтому, любое непустое множествоимеет, по крайней мере, два различных подмножества: самои пустое множество.

Эти подмножества называются несобственными, а все другие подмножества называютсясобственными. Если требуется различать собственные и несобственные подмножества, то для обозначения включения собственных подмножеств используется знак (), а для несобственных –().

Конечно, собственные подмножества образуются всевозможными сочетаниями по одному, два, три и т.д. элементов данного множества.

Пример: ;;;;;;., где.

Определение. Множество всех подмножеств множества , илибулеан множества , обозначаемый (или), есть множество, состоящее из всех подмножеств множества. Множествоназывается такжемножеством-степенью.

Пример. Так, для трёхэлементного множества булеан имеет вид.

В случае конечного множества , состоящего изn элементов, множество подмножеств содержитэлементов, т.е..

Пустое множество имеет только одно подмножество – само пустое множество, поэтому .

1.8. Контрольные вопросы и задания

1. Что такое множество? Приведите примеры различных множеств.

2. Какие способы задания множеств Вы знаете?

3. Что такое пустое множество? Обоснуйте необходимость использования пустого множества.

4. Что такое универсальное множество? Приведите примеры универсального множества.

5. Дайте определение конечного и бесконечного множества.

6. Дайте определение счетного множества.

7. Что такое мощность множества?

8. Дайте определение подмножества. Приведите примеры подмножеств.

9. Какое отношение между множествами называют строгим включением?

10. Чем отличается понятие включения (или) от понятия принадлежности ()?

11. В каких случаях можно говорить, что множества ,иравны?

12. Поясните понятие «булеан множества ». Приведите примеры булеана.

Лекция 2Алгебра множеств

2.1 Геометрическая интерпретация множеств. Круги Эйлера и диаграммы Венна

Для наглядного представления отношений между подмножествами универсального множества используются диаграммы Венна и круги Эйлера.

Построение диаграммы Венна заключается в разбиении плоскости на ячеек с помощьюфигур, каждая из которых представляет на диаграмме отдельное множество, а– число изображаемых множеств.

Плоскость, на которой изображаются фигуры, представляет универсальное множество. Чаще всего универсальное множество при этом изображают в виде прямоугольника, а его подмножества изображают в виде кругов (кругов Эйлера), находящихся внутри прямоугольника.

С помощью диаграмм Эйлера-Венна можно графически показать, принадлежит ли некоторый элемент рассматриваемым множествам или нет, однако реальные отношения включения, установленные между множествами, отразить нельзя. Можно рассматривать отношения включения только в общем случае.

Пример. На рис. 1.1 элемент принадлежити не принадлежит;принадлежити;принадлежити не принадлежит;не принадлежит ни, ни. Любой элемент принадлежит универсальному множеству.

Рисунок 1.1 – Диаграмма Венна для двух множеств и

Индивидуальные отношения между заданными множествами изображают с помощью кругов Эйлера. В этом случае множества, не имеющие общих элементов, изображают фигурами (чаще кругами), которые не пересекаются (рис. 1.2).

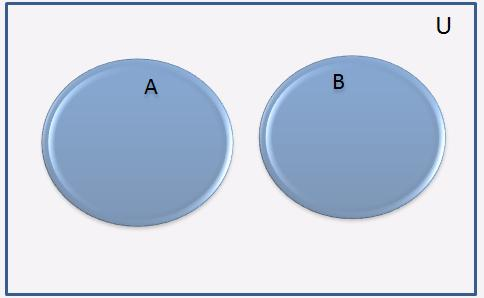
Рисунок 1.2 – Изображение множеств, не имеющих общих элементов, с помощью кругов Эйлера

Множества, имеющие общие элементы, изображают пересекающимися фигурами (рис. 1.3).

Рисунок 1.3 – Изображение множеств, имеющих общие элементы, с помощью кругов Эйлера

Отношение включения на множествах изображают, располагая одну фигуру вложенной в другую (рис. 1.4).

Рисунок 1.4 – Изображение отношения включения на множествах с помощью кругов Эйлера

2.2 Операции на множествах

В теории множеств определяются способы конструирования новых множеств из уже имеющихся при помощи операций над множествами. К таким основным (базовым) операциям на множествах относятся следующие операции: объединение, пересечение, разность, дополнение.

Рассмотрим операции на множествах.

Пусть имеются два множества и.

Определение. Объединением (суммой) множеств иназывается множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множествили. Объединение множествиобозначается. Данное определение можно записать.

Пример:

а) если , а, тогда. Объединениеобразовано изипутем соединения вместе элементови.

б) если ,, то.

Аналогично определяется объединение произвольной (в том числе бесконечной) совокупности множеств. Если совокупность содержит небольшое количество множеств, то объединение данных множеств описывается явно, т.е. и т.д.

В общем случае используется обозначение , которое читается так: «объединение всех множеств, принадлежащих совокупности».

Если же все множества совокупности занумерованы индексами, то используются другие варианты обозначений:

а)  для случая, когда;

б)  для случая, когда– бесконечная совокупность и её множества занумерованы подряд натуральными числами;

в)  для случая, когда набор индексов множеств задан множеством.

Определение. Пересечением множеств иназывается множество, состоящее из всех тех и только тех элементов, которые принадлежат и, и. Пересечение множествиобозначается.

Сформулированное определение можно записать как . Если, тои– непересекающиеся множества.

Пример:

1. Если и, тогда.

2. Если и

, тогда

.

Аналогично определяется пересечение произвольной (в том числе бесконечной) совокупности множеств. Обозначение для пересечения системы множеств аналогичны приведенным выше обозначениям для объединения.

Определение. Система множеств, в которой все попарные пересечения множеств пусты, называется разбиением множества всех элементов этих множеств, а множества такой системы называютсяклассами или блоками разбиения. Всякий элемент множества входит только в один класс разбиения.

Пример:

Множество всех групп направления (потока) «Компьютерные науки» является разбиением множества всех студентов, поступивших в университет на направление «Компьютерные науки». Классы этого направления – группы. Всякий студент может входить только в одну группу.

Определение. Разность и(обозначаетсяили)  это множество, состоящее из тех и только тех элементов, которые принадлежати не принадлежат, т.е..

Пример: ;; тогда , .

Определение. Если , то множествоназываетсядополнением (абсолютным дополнением, отрицанием) множества .

Дополнение множества , обозначаемое(читается «не»), – это множество элементов универсума, которые не принадлежат, следовательно,. Дополнениеопределяется отрицанием свойства, с помощью которого определяется.

Пример:

Если – множество положительных целых чисел, а– множество всех положительных четных чисел, то– множество всех положительных нечетных чисел.

Определение. Дизъюнктивная сумма (симметрическая разность) – это множество, состоящее из всех элементов , не принадлежащих, и всех элементов, не принадлежащих, и не содержащее никаких других элементов, т.е..

Симметрическая разность, обозначаемая как , либо, либо, получается объединением элементов множеств за исключением тех, которые встречаются дважды.

Пример: ;;.

Еще одной часто используемой операцией над множествами является декартово произведение. Обозначение и суть данной операции будут рассмотрены в разделе, связанном с описанием отношений.

Введенные операции называются теоретико-множественными операциями.

Все данные операции на множествах можно проиллюстрировать с помощью диаграмм Эйлера-Венна (рис. 1.5), в которых круги представляют соответствующие множества, участвующие в операциях (например, множество ), а заштрихованная часть плоскости является результатом выполнения операций (например,,,,,).

а) б)

в) г)

д) е)

Рисунок 1.5  Применение диаграмм Эйлера-Венна для иллюстрации операций на множествах

2.3 Общее определение алгебры

Алгебра в широком понимании может быть определена как наука (учение) о системах объектов той или иной природы, в которых установлены алгебраические операции. Для современной алгебры характерно то, что в центре внимания оказываются свойства операций, а не объектов, над которыми производятся эти операции. Алгебра классифицирует системы с заданными на них алгебраическими операциями по их свойствам и изучает различные задачи, естественно возникающие в этих системах.

Введем формализованное понятие алгебры.

Определение. Множество вместе с заданной на нем совокупностью операций, т.е. система, называетсяалгеброй. Множество – этоосновное, или несущее, множество (или просто носитель) алгебры. называетсясигнатурой и представляет собой множество операций с элементами множества . Функция типа:называется-арной операцией. Вектор арностей операций алгебры называется её типом.

Определение. Операция, заданная на некотором множестве, называется бинарной, если она действует на два элемента этого множества и её результатом является элемент этого же множества.

Определение. Операция, заданная на некотором множестве, называется унарной, если она действует на один элемент множества и её результатом является элемент этого же множества.

Нульарные операции – это фиксированные элементы множества , называются такжевыделенными элементами, иногда нулями.

Определение. Множество называетсязамкнутым относительно -арной операции на , если , т.е. если значенияна аргументах изпринадлежат. Еслизамкнуто относительно всех операцийалгебры, то системаназываетсяподалгеброй (при этомрассматриваются как операции на).

Примеры алгебр:

1. Алгебра называется полем действительных чисел. Несущее множество– множество действительных чисел. Операции + и– бинарные операции, поэтому тип этой алгебры. Подалгеброй этой алгебры является, например, поле рациональных чисел.

2. Пусть задано множество . Множество всех его подмножеств является булеаноми обозначается. Алгебраназывается булевой алгеброй множеств над, её тип. Элементами несущего множества этой алгебры являются множества (подмножества). Для любогоявляется подалгеброй. Например, если, то основное множество алгебрысодержит 16 элементов; алгебра– подалгебра; её основное множество содержит четыре элемента. Операцииявляются бинарными, а операция отрицанияявляется унарной.

2.4 Понятие алгебры множеств. Аксиомы алгебры множеств

Алгебра множеств представляет собой теоретико-множественный аналог обычной алгебры действительных чисел и основана на свойствах операций над множествами.

Определение. Алгебра множеств – непустая совокупность подмножеств некоторого множества , замкнутая относительно теоретико-множественных операций (объединения, пересечения, разности, дополнения).

Для того чтобы некоторый класс подмножеств множества был алгеброй множеств, достаточно (и необходимо), чтобы он был замкнут относительно образования объединений и дополнений.

Операции над множествами, как и операции над числами, обладают некоторыми свойствами. Эти свойства выражаются совокупностью формул и тождеств, справедливых независимо от конкретного содержания входящих в них множеств. Данные тождества основаны на следующих аксиомах (законах) алгебры множеств, где рассматриваются как произвольные подмножества универсального множества:

1. Коммутативные законы

,

.

2. Ассоциативные законы

,

.

3. Дистрибутивные законы

,

.

4. Свойства пустого и универсального множеств

, ,

, .

, .

5. Законы идемпотентности (самопоглощения)

,

.

6. Закон инволюции

.

7. Закон противоречия

.

8. Закон исключенного третьего

.

9. Законы элиминации (поглощения)

.

.

10.Законы де Моргана

,

.

Свойствами дополнения, разности и равенства также являются:

11. Если .

12. .

13. .

В справедливости перечисленных выше свойств можно убедиться различными способами:

• нарисовать диаграммы Эйлера-Венна для левой и правой частей равенства и убедиться, что они совпадают;

• провести формальные рассуждения для каждого равенства.

2.5 Принцип двойственности

Практически все рассмотренные тождества (законы алгебры множеств) представлены парами двойственных (дуальных) соотношений, одно из которых получается заменой в другом следующих символов: наина, а такженаина.

Определение. Соответствующие пары символов ,и,называютсядвойственными (дуальными) символами.

При замене в любом законе входящих в него символов дуальными получим новое предложение, которое также является законом. Данное утверждение представляет собой принцип двойственности или дуальности. Законы 11 и 12 не изменяются при замене символов дуальными, поэтому их называют самодвойственными.

Расширяя принцип дуальности на выражения, в которые входит символ включения, необходимо при переходе к дуальному выражению все знаки заменить наи обратно.

2.6 Тождественные преобразования формул алгебры множеств

Пользуясь основными тождествами (законами) можно упрощать или преобразовывать к удобному виду различные сложные выражения, содержащие множества, аналогично тому, как проводится упрощение выражений в элементарной алгебре. Для выполнения подобных преобразований применяется следующая приоритетность операций относительно друг друга: ,,,.

Такие преобразования осуществляются последовательным применением соответствующих свойств операций над множествами.

Пример. Соотношение доказывается следующими преобразованиями с использованием рассмотренных законов

.

Пример. Упростить выражение .

Для упрощения используем законы алгебры множеств.

=.

Важно отметить, что любое тождество алгебры множеств выводимо из первых четырех свойств, которые в свою очередь доказываются только в терминах отношения принадлежности. Это можно рассматривать как иллюстрацию аксиоматического подхода к алгебре множеств.

2.7 Контрольные вопросы и задания

1. Какие операции над множествами позволяют строить новые множества, используя уже существующие?

2. Какова приоритетность выполнения операций над множествами.

3. Какие способы графической иллюстрации операций над множествами Вы знаете?

4. Поясните обобщенное понятие алгебры. Приведите примеры алгебр.

5. Что такое алгебра множеств?

6. Какая операция над множествами называется бинарной?

7. Какая операция над множествами называется унарной?

8. Назовите основные аксиомы алгебры множеств.

9. Какими свойствами обладает пустое множество и универсальное множество?

10. Опишите принцип двойственности в алгебре множеств, приведите примеры двойственных символов.

11. Поясните способы преобразования формул алгебры множеств.

Лекция 3 Отношения и их свойства. Отношения и операции над ними.

3.1 Декартово произведение множеств

Для формального определения понятия отношения используем понятие декартова (прямого) произведения множеств.

Определение. Декартовым (прямым) произведением множеств иназывается множество, которое обозначаетсяи состоит из всех тех и только тех упорядоченных пар, первая компонента (координата) которых принадлежит множеству, а вторая компонента (координата) принадлежит множеству, т.е..

Пример.

Пусть , . Тогда .

Порядок следования пар может быть произвольным, но размещение элементов в каждой паре определяется порядком следования перемножаемых множеств. Следовательно, декартово произведение изменяется при смене порядка сомножителей, и , если.

Пример. Пусть ,.

.

.

Следовательно, .

Операция декартова произведения легко расширяется и на большее число множеств.

Определение.

Декартовым произведением множеств называется множество всех возможных упорядоченных наборовизэлементов (кортежей), в которых первый элемент (первая координата) принадлежит множеству, второй (вторая координата) множеству ,-й (-ая координата) множеству , т.е..

Пример.

Пусть ,,.

Тогда

Если или, то, так как не существует упорядоченных пар с отсутствующей первой или второй координатой. Аналогичнотогда и только тогда, когда хотя бы одно из множествявляется пустым множеством.

Отдельным случаем операции декартова произведения является понятие степени множества.

Определение.

Декартово произведение , в котором одно и то же множествоумножаетсяраз само на себя, называетсядекартовой степенью множества и обозначается . При этом. Множествоназываетсядекартовым квадратом множества , множество декартовым кубом множества .

Пример. Пусть , тогда,,.

Пример.

Пусть  множество действительных чисел, тогда множество  множество точек на плоскости.

Определим мощность декартова произведения, используя теорему 3.1.

Теорема 3.1.

Пусть  конечные множества и ,, …,. Тогда мощность декартова произведенияравна произведению мощностей.

Доказательство теоремы можно провести методом математической индукции.

Следствие теоремы 1. Мощность декартовой степени множества равна.

Пример. Пусть ,,.

Мощность множества равна, где,,.

Мощность множества равнаили

3.2 Понятие отношений. Бинарные иn-арные отношения

Введем формальные понятия отношений.

Говорят, что находятся в отношении(является множеством), если.

Определение. -арное (-местное) отношение на множествах это подмножество декартова произведения этих множеств, т.е..

Определение. Унарное (одноместное) отношение – это подмножество множества. Такие отношения называются признаками:обладает признаком, еслии.

Свойства унарных (одноместных) отношений – это свойства подмножеств множества . Поэтому для случаятермин «отношение» употребляется редко.

Пример.

Тернарным (трехместным) отношением являются: арифметические операции над числами; отношение между родителями и детьми (отец, мать, ребенок); множество троек нападающих в хоккейной команде.

Пропорция иллюстрирует четырехместное отношение.

Наиболее часто встречающимися и хорошо изученными являются бинарные, или двухместные, отношения. Эти отношения возникают между парами объектов.

Определение.

Бинарным отношением на паре множеств ибудем называть подмножество декартового произведения.

Пример. Отношение принадлежности (определяет связь между множеством и его элементами, обозначается ); отношение включения (определяет связь между двумя множествами); отношение равенства (=); отношение неравенства (или).

Примеры бинарных отношений.

1. Выражения: «быть братом», «делиться на какое-либо число»; «входить в состав (чего-либо)».

2. Всё множество есть отношение множестви.

3. Если  множество действительных чисел, то {}.

4. Пусть  множество товаров в магазине, а  множество действительных чисел. Тогда  отношение множеств и.

5. Отношение «» выполняется для пар (7,9) и (7,7), но не выполняется для пары (9,7).

6. Если  множество людей, то .

Для любого бинарного отношения можно записать соответствующее ему соотношение. В общем виде соотношение можно записать как , где отношение, устанавливающее связь между элементом из множестваи элементомиз множества.

Определение. Пусть ,,. На паре множествиможно построитьбинарных отношений.

Определение. На множестве , состоящем изэлементов, может быть заданобинарных отношений.

В дальнейшем будем рассматривать бинарные отношения, поэтому вместо термина «бинарное отношение» будем употреблять термин «отношение».

3.3 Область определения и область значений отношений

Определение.

Область определения отношения наи(обозначим) есть множество всехтаких, что для некоторыхимеем, т.е. область определенияесть множество первых координат упорядоченных пар из.Область значений отношения наи(обозначим) есть множество всехтаких, чтодля некоторого, т.е. область значений есть множество всех вторых координат упорядоченных пар из.

Пример.

В примерах отношений, приведенных выше, в частности, в (2), область определения есть все множество , а область значений все множество . В (3) как область определения, так и область значений совпадают с множеством. В (4) область определения есть множество, а область значений есть множество всех действительных чисел, каждое из которых совпадает с ценой некоторого товара в магазине. В (6) область определения и область значений есть множество всех людей, имеющих родственников.

Пример. и. Декартово произведение этих множеств.

Отношение «быть делителем» есть множество . Отношение «равенство (=)» есть множество. Отношение «» есть пустое множество.

Области определения и значений отношения  это соответственно множества и .

Области определения и значений отношения  это соответственно множества , и .

Определение. Если и, тои . В таких случаях есть отношение отк, называетсясоответствием и обозначается . Если, то любоеявляется подмножеством множестваи называетсяотношением в .Если область определения отношения совпадает с некоторым множеством , то говорят, что отношениеопределено на .

Существует три частных случая отношений в :

• полное (универсальное отношение) 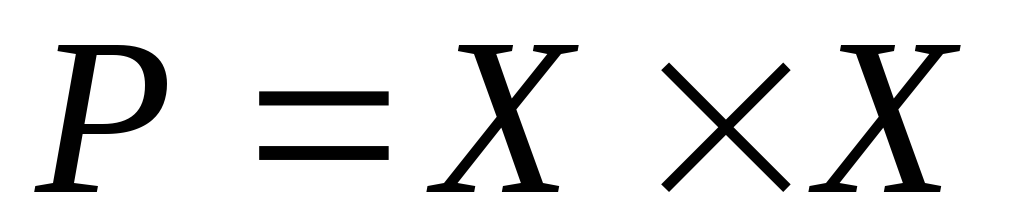, которое имеет место для каждой парыэлементов из(например, отношение «работать в одном отделе» на множестве сотрудников данного отдела);

• тождественное (диагональное) отношение, равносильное (например, равенство на множестве действительных чисел);

• пустое отношение, которому не удовлетворяет ни одна пара элементов из (например, отношение «быть братом» на множестве женщин).

3.4 Способы задания отношений

Существует несколько способов задания отношений:

• способ перечисления элементов (в виде списка);

• способ задания характеристического свойства или (порождающей процедуры), выраженного в словесной или символической форме;

• матричный способ;

• графический способ (с помощью ориентированного графа);

• с помощью фактор-множества.

Отношение полностью определяется множеством всех пар элементов , для которых оно имеет место. Поэтому любое бинарное отношениеможно рассматривать как множество упорядоченных пари задавать его в виде списка этих пар.

Пример. На множествах чисел ипостроим отношение «делитель» (), которое состоит из упорядоченных пар вида, где делитель ,,:

.

Часто отношение задается при помощи характеристического свойства, выраженного в словесной или символической форме.

Пример. Пусть  множество женщин,  множество мужчин. Тогда отношение , заданное при помощи характеристического свойства, выраженного в словесной форме, будет иметь вид.

Пример. Если  множество действительных чисел, то .

Матричный способ задания отношений основан на представлении отношения соответствующей ему прямоугольной таблицей (матрицей). Её строки соответствуют первым координатам, а столбцы – вторым координатам. На пересечении -ой строки и-ого столбца ставится единица, если выполнено соотношение, и нуль, если это соотношение не выполняется (нулевые клетки можно оставлять пустыми).

Эта матрица содержит всю информацию об отношении .

Полному отношению соответствует квадратная матрица, все клетки которой заполнены единицами, тождественному – квадратная матрица, состоящая из нулей, с главной диагональю из единиц, а пустому – квадратная нулевая матрица.

Пример. Пусть заданы ,. Отношениеможет быть представлено следующей матрицей

	1		1
	1		1	1
	1	1		1
			1
		1		1

Отношения можно задавать (или изображать) с помощью ориентированного графа. Вершины графа соответствуют элементам множеств и(элементы изображаются точками на плоскости), а дуга, направленная из вершинык(направленная линия, соединяющая пары точек) означает, что.

Пример. Отношение из предыдущего примера представлено в виде следующего ориентированного графа (рис.3.1).

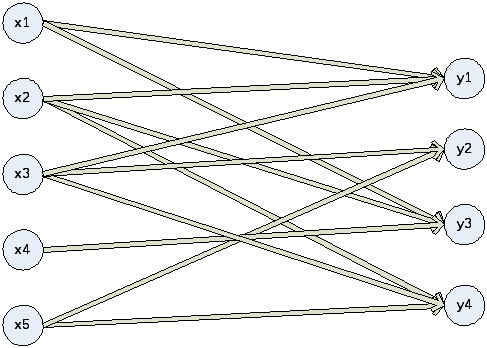
Рисунок 3.1 – Граф отношения

Отношение в отображается графом с вершинами, соответствующими элементам этого множества. При этом если имеют место соотношенияи, то вершины связываются двумя противоположно направленными дугами, которые можно условно заменять одной ненаправленной дугой. Соотношениюсоответствует петля, выходящая изи входящая в эту же вершину.

Пример. Пусть . Отношениеможет быть представлено в виде графа на рис. 3.2.

Рисунок 3.2 – Граф отношения

Пример.

Граф полного отношения для представлен в следующем виде (рис. 3.3).

Рисунок 3.3 – Граф полного отношения для

Пример.

Граф тождественного отношения для представлен в следующем виде (рис. 3.4).

Рисунок 3.4 – Граф тождественного отношения для

Пример.

Граф пустого отношения для представлен в следующем виде (рис. 3.5).

Рисунок 3.5 – Граф пустого отношения для

При рассмотрении способа задания отношения с помощью фактор-множества введем понятие сечения отношения.

Определение

Пусть  отношение на множествах и. Если, тосечение отношения по элементу, обозначаемое, есть множество, состоящее из элементовтаких, что, т.е.. Множество всех сечений отношенияназываетсяфактор-множеством множества по отношениюи обозначают. Объединение сечений по элементам некоторого подмножестваназываетсясечением R(Z) относительно подмножества Z.

Фактор-множество полностью определяет отношение .

Пример. Пусть заданы множества ,и отношение. Получим сечения:,,,,,. Определим фактор-множество. Рассмотрим множество. Сечение отношенияпо множествувыглядит следующим образом:.

3.5 Операции над отношениями

Так как отношения – это множества, то над ними могут выполняться все теоретико-множественные операции: объединение, пересечение, дополнение и разность.

Кроме того, определяются специфические для отношений операции: сечение, обращение (симметризация) и композиция.

Рассмотрим два отношения и, определенные на множествахи,,. В результате выполнения операций,,получаем множество упорядоченных пар, являющихся соответственно объединением, пересечением и разностью множестви. Результаты выполнения этих операций также являются отношениями на множествахи. Дополнение отношения(обозначается) содержит все упорядоченные пары множества, кроме тех пар, которые принадлежат, т.е..

Пример. Пусть заданы множества ,и отношения на них,.

Тогда ;;;;

;

.

Пример операции сечения отношений приведен выше.

Рассмотрим операцию обращения (симметризации) отношений.

Определение

Отношение, симметричное (обратное) некоторому отношению , обозначаетсяи представляет собой подмножество множества, образованное теми парами, для которых.

Если , то, если, то.

Переход от косуществляется взаимной перестановкой координат каждой упорядоченной пары.

Пример. Отношение  «делитель», а обратное к нему «кратно».

Пусть ,иотношение «быть делителем» отк. Тогдаи.

При переходе от кобласть определения становится областью значений и наоборот. Матрица транспонированная матрица отношения . Граф обратного отношения находится из исходного графа заменой направлений всех дуг на противоположные.

Рассмотрим операцию композиции отношений, которая позволяет получить отношение из двух других отношений.

Пусть даны три множества и два отношенияи.

Определение

Композиция отношений иесть отношение, состоящее из всех тех пар, для которых существует такое, чтои.

Композиция отношенийиобычно обозначается как(или).

Пример. Пусть заданы два отношения:

и .

Очевидно, что композиция будет представлена следующим образом

Композиция отношений имеет следующие свойства:

• , т.е. закон коммутативности не выполняется;

• , т.е. закон ассоциативности выполняется;

• ;

• .

Композиция отношений и, где множества, наглядно представляется с помощью графов. Прежде всего, необходимо к графу отношения достроить граф отношения. Граф отношенияможет быть получен при исключении вершин, соответствующих элементам множества. При исключении вершиныкаждый проходящий через неё путь от вершинк вершинамзаменяется одной дугой с тем же направлением. Параллельные ветви с одинаковыми направлениями соответствуют одинаковым парам ви рассматриваются как одна ветвь.

Пример. Пусть заданы множества ,и, а также отношенияи. Построим отношение.

Построим граф отношения и достроим к нему граф отношения(рис. 3.6).

Рисунок 3.6  Граф отношения и отношения

Исключим вершины и каждый проходящий через неё путь от вершинк вершинамзаменим одной дугой с тем же направлением, получим граф отношения(рис. 3.7).

Рисунок 3.7  Граф отношения

Аналогично можно получить матрицу композиции как произведение матриц отношенийи(в порядке их следования), которое выполняется по обычному правилу умножения прямоугольных матриц с последующей заменой отличного от нуля элемента результирующей матрицы единицей.

3.6 Контрольные вопросы и задания

1. Как связаны между собой теория множеств и теория отношений?

2. Поясните понятие кортежа. Приведите примеры кортежей.

3. Что такое прямое (декартово) произведение множеств?

4. Как определяется мощность декартового произведения?

5. Что такое отношение множеств?

6. Какое отношение называется -арным, унарным, бинарным?

7. Что такое тождественное отношение, полное отношение, нулевое отношение?

8. Пусть  некоторое множество. Что означает запись ,,,?

9. Что является областью определения и областью значения отношения ?

10. Назовите способы задания отношений.

11. Какие из способов задания отношений применимы для -арных отношений при?

12. Перечислите операции, производимые над отношениями.

13. Дайте определение сечения отношения по элементу.

14. Что такое фактор-множество множества по отношению?

15. Назовите специфические операции над отношениями.

16. Что такое композиция отношений?

17. Что такое симметризация отношений?

18. Какое отношение называется обратным?

Лекция 4 Свойства бинарных отношений

4.1 Основные свойства бинарных отношений

Отношения могут обладать некоторыми общими свойствами (например, отношение включения и отношение равенства транзитивны). Определяя эти свойства и комбинируя их, можно выделить важные типы отношений, изучение которых в общем виде заменяет рассмотрение огромного множества частных отношений.

Пусть  бинарное отношение в множестве . Определим общие свойства таких отношений, которые должны выполняться для всех:

• рефлексивность;

• антирефлексивность;

• симметричность;

• асимметричность;

• антисимметричность;

• транзитивность;

• антитранзитивность.

Определение. Отношение называетсярефлексивным, если принадлежитдля всехиз, т.е. оно всегда выполняется между объектом и им самим ().

Для рефлексивного отношения все элементы матрицы на главной диагонали равны 1. Граф рефлексивного отношения содержит петли у всех вершин.

Определение. Отношение называетсяантирефлексивным, если ( тождественное отношение), т.е. может выполняться только для несовпадающих объектов: из следует.

Для антирефлексивного отношения все элементы матрицы на главной диагонали равны 0. Граф антирефлексивного отношения не содержит петель у вершин, нет дуг вида .

Примеры.

Отношение равенства («=»), отношение «» на множестве вещественных чисел, отношение «иметь общий делитель» на множестве целых чисел рефлексивны.

Отношение «» на множестве вещественных чисел, отношения «быть сыном», «быть старше» на множестве людей антирефлексивны.

Отношение «быть симметричным относительно оси на множестве точек координатной плоскости» не является ни рефлексивным, ни антирефлексивным: точка плоскости симметрична сама себе, если она лежит на оси, и несимметрична сама себе в противном случае.

Определение. Отношение называетсясимметричным, если , т.е. при выполнении соотношениявыполняется и соотношение(выполняется либо в обе стороны, либо не выполняется вообще).

Симметричность отношения влечет и симметричность матрицы.

Для симметричного отношения вершины графа могут быть связаны только парами противоположно направленных дуг (ненаправленными ребрами).

Определение. Отношение называетсяасимметричным, если , т.е. из двух соотношенийипо меньшей мере одно не выполняется. Если отношение асимметрично, то оно и антирефлексивно.

Матрица асимметричного отношения характеризуется тем, что у неё нулевые элементы на главной диагонали и нет ни одной пары единиц, стоящих на симметричных относительно главной диагонали местах (несимметричность матрицы).

В графе асимметричного отношения петли отсутствуют, а вершины могут быть связаны только одной направленной дугой.

Определение. Отношение называетсяантисимметричным, если ( тождественное отношение), т.е. оба соотношения ивыполняются одновременно только тогда, когда

Матрица антисимметричного отношения является несимметричной, но на главной диагонали могут находиться как 0, так и 1.

В случае антисимметричного отношения в графе могут быть петли, но связь между вершинами, если она имеется, отображается только одной направленной дугой.

Пример. Расстояние между двумя точками на плоскости, отношение «быть братом» в множестве людей являются примерами симметричного отношения.

Отношение строгого включения в множестве всех подмножеств некоторого универсума и отношение «быть отцом» в множестве людей являются асимметричными.

Отношение нестрогого включения в множестве всех подмножеств некоторого универсума, отношения нестрогого неравенства «» и «» на множестве целых, действительных чисел являются антисимметричными.

Определение. Отношение называетсятранзитивным, если , т.е. изиследует.

В матрице транзитивного отношения для каждой пары единичных элементов, один из которых расположен в -й строке и-м столбце, а другой в-й строке и-м столбце, обязательно существует единичный элемент, расположенный в клетке на пересечении-й строки и-ого столбца (наличие единичных элементов на главной диагонали не нарушает транзитивности).

Наглядно проявляется на графе свойства транзитивности: если через некоторую совокупность вершин графа проходит путь, то существуют дуги, соединяющие любую пару вершин из этой совокупности. Обычно в графе транзитивного отношения изображают только этот путь, а обусловленные транзитивностью дуги опускают. Такой упрощенный граф называют графом редукции.

Определение. Отношение называетсяантитранзитивным, если из иследует, что не выполняется.

Примеры. Отношения «равенство», «быть делителем», заданные на множестве целых чисел, и отношение «жить в одном городе», заданное на множестве людей являются транзитивными.

Отношение «быть сыном» на множестве людей является антитранзитивным.

4.2 Классы бинарных отношений

4.2.1 Отношение эквивалентности

Отношение эквивалентности представляет собой экспликацию (перевод интуитивных представлений в ранг строгих математических понятий) таких обыденных слов как «одинаковость», «неразличимость», «взаимозаменяемость».

Определение. Бинарное отношение в множестве называется отношением эквивалентности (обозначается ~), если для него выполняются следующие свойства:

• рефлексивность ();

• симметричность (если , то);

• транзитивность (из ) иследует.

Примеры отношений эквивалентности:

• «проживать в одном доме » в множестве людей;

• «подобие треугольников» в множестве всех треугольников на плоскости;

• «параллельность прямых» в множестве всех прямых на плоскости.

Важнейшее значение эквивалентности состоит в том, что это отношение определяет признак, который допускает разбиение множества на непересекающиеся подмножества, называемыеклассами эквивалентности. Наоборот, всякое разбиение множества на непересекающиеся подмножества определяет между элементами этого множества некоторое отношение эквивалентности.

Теорема 4.1

Если на множестве задано отношение эквивалентности, то это отношение задает разбиение множества и это разбиение единственно.

Все элементы, принадлежащие некоторому классу разбиениямножества, связаны между собой отношением эквивалентности. Они взаимозаменяемы в том смысле, что любой из этих элементов определяет данный класс, т.е. может служить его представителем (эталоном). Каждый класс отождествляется с некоторым общим свойством или совокупностью свойств (параметров) входящих в него элементов.

Подмножество из , содержащее по одному и только одному элементу из каждого класса некоторого разбиения, называютсистемой представителей соответствующего отношения эквивалентности. Множество всех классов разбиения множества , определяемого отношением эквивалентности, образует фактор-множество.

Предельным случаем отношения эквивалентности является тождественное равенство. Единственный элемент, равный какому-либо данному элементу, есть этот самый элемент. Следовательно, имеем самое полное разбиение, при котором классы эквивалентности содержат только по одному элементу исходного множества.

Пример. Отношение «проживать» в множестве жителей города является эквивалентностью и разбивает это множество на непересекающиеся подмножества людей, являющихся соседями по дому.

Пример. Отношение параллельности определяет разбиение множества прямых на плоскости на классы, каждый из которых образован множеством параллельных между собой прямых и характеризуется некоторым направлением (следует также считать, что прямая параллельна самой себе). Любая из параллельных прямых может служить представителем данного класса, а само направление есть класс эквивалентности. Множество всех направлений составляет фактор-множество множества всех прямых по отношению параллельности.

Элементы, принадлежащие одному классу эквивалентности, попарно эквивалентны между собой, следовательно, столбцы матрицы отношения эквивалентности для элементов одного класса эквивалентности одинаковы и содержат единицы во всех строках, которые соответствуют этим элементам. Так как классы эквивалентности не пересекаются, то в столбцах, соответствующих элементам различных классов, не будет единиц в одних и тех же строках.

При построении матрицы отношения расположим элементы множества так, чтобы элементы, принадлежащие одному классу эквивалентности, стояли рядом. Тогда единичные элементы матрицы отношения эквивалентности образуют непересекающиеся квадраты, диагонали которых располагаются на главной диагонали матрицы.

Пример Для отношения эквивалентности, заданного классами эквивалентности ;;, матрица будет иметь вид

	1	1	1
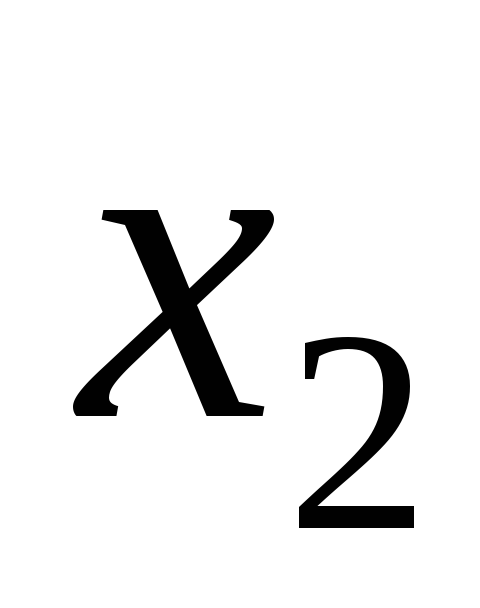
	1	1	1
	1	1	1
				1	1
				1	1
						1	1	1	1
						1	1	1	1
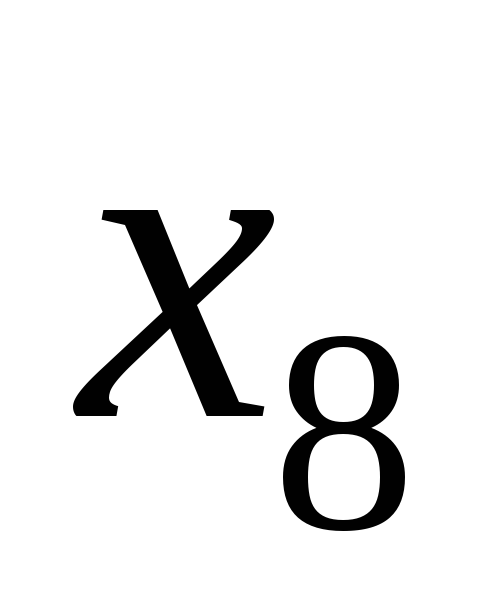
						1	1	1	1
						1	1	1	1

Граф отношения эквивалентности тоже имеет характерный вид. Он представляет собой граф, каждая компонента связности которого, соответствующая классу эквивалентности, является полным графом с петлями на каждой вершине. Для данного примера граф имеет вид, представленный на рис. 4.1.

Рисунок 4.1  Граф отношения эквивалентности

4.2.2 Отношение порядка

Определим различные варианты (типы) отношений порядка (отношение частичного, нестрого, строгого, полного, линейного порядка). Отношение порядка позволяет сравнивать между собой различные элементы одного множества.

Отношение порядка в общем случае обозначается .

Определение

Множество, в котором определено отношение порядка, называется упорядоченным (порядок введен этим отношением).

Определение

Отношение в множественазываетсяотношением частичного (нестрогого) порядка, если для любых извыполняются свойства:

• рефлексивности ();

• антисимметричности (из иследует);

• транзитивности (если и, то).

Частичный порядок принято обозначать символом , а обратное ему отношениепринято обозначать символом.

Определение

Если на множестве задано отношение частичного порядка, то это множество называется частично упорядоченным.

Пример. Отношением частичного порядка в множестве людей можно назвать отношение «быть не старше» или «быть не моложе».

Отношением частичного порядка в множестве целых чисел является отношение «быть делителем» (очевидно, что не все пары элементов из множества целых чисел находятся в данном отношении)

Булеан , т.е. множество всех подмножеств некоторого множества, является частично упорядоченным множеством с отношением теоретико-множественного включения, как отношения частичного порядка.

Определение

Элементы иназываютсясравнимыми в отношении частичного порядка , если выполняется хотя бы одно из соотношенийили. Если для некоторых парни одно из соотношенийилине имеет места, то такие элементы называютнесравнимыми.

Пример. Пусть  множество положительных делителей числа 30, а есть отношение частичного порядка (), еслиделитнацело. Целые числа 5 и 15 сравнимы, поскольку 5 делит 15 нацело, а 5 и 6 несравнимы.

Определение

Частичный порядок называется линейным (полным) порядком, если любые два элемента ииз множествасравнимы, т.е.и.

Определение

Множество , на котором задано отношение частичного порядкаи для которого любые два элемента этого множества сравнимы, называетсялинейно упорядоченным, полностью упорядоченным или цепью.

Пример. Множество натуральных или действительных чисел с естественным отношением порядка , множество точек числовой оси (прямой), множество значений длин волн на шкале радиоприемника являются линейно упорядоченными.

Линейно упорядоченное (полностью упорядоченное) множество отличается от частично упорядоченного тем, что в частично упорядоченном множестве могут присутствовать элементы, из которых можно составить несравнимые пары.

Любое частично упорядоченное множество наглядно можно представить в виде схемы, которая называется диаграммой Хассе. Каждый элемент на плоскости изображается точкой, и любую пару точек, соответствующих элементами, соединяют стрелкой, идущей из точкив точку, тогда и только тогда, когда,, и не существуеттакого, что, и элементотличается и от, и от.

Пример. Пусть  линейно упорядоченное множество с обычным отношением порядка на множестве натуральных чисел, не превосходящих пяти. Элементы этого отношения упорядочены обычным отношением частичного порядка .

Его диаграмма Хассе изображена на рис. 4.2.

Рисунок 4.2  Диаграмма Хассе

Рассмотрим отношения нестрогого и строгого порядка.

Определение

Отношение частичного порядка, являющееся рефлексивным, антисимметричным и транзитивным, называется также отношением нестрогого порядка.

Определение

Отношение в множественазываетсяотношением строгого порядка (его принято обозначать символом < ), если оно:

• антирефлексивно (если , то);

• асимметрично (если , то не верно)

• транзитивно (если и, то).

Это отношение не является частичным порядком, т.к. не удовлетворяет условию рефлексивности .

Пример. В качестве примера отношения строгого порядка можно привести отношение «» или «» в множестве(множество натуральных чисел) или(множество действительных чисел), а также отношения «быть старше» или «быть моложе» в множестве людей.

Отношение строгого порядка характерно для различного рода иерархий с подчинением одного объекта другому (или другим)

Матрица отношения нестрогого порядка представлена следующим образом:

• главная диагональ матрицы этого отношения заполнена единицами (свойство рефлексивности);

• ни один единичный элемент не имеет симметричного себе элемента относительно главной диагонали (свойство антисимметричности);

• наличие единиц на пересечении -го столбца и-й строки, и единицы на пересечении-го столбца и-й строки, влечет за собой наличие единицы на пересечении-го столбца и-й строки (свойство транзитивности).

Матрица отношения строгого порядка отличается тем, что все элементы главной диагонали нулевые (свойство антирефлексивности).

Граф нестрогого порядка не содержит параллельных и противоположно направленных дуг, с каждой вершиной связана петля, а также все вершины любого пути попарно связаны между собой дугами в направлении этого пути.

Граф строгого порядка отличается тем, что в нем отсутствуют петли.

4.2.3 Отношение толерантности

Определение

Отношение толерантности на множествеудовлетворяет свойствам:

• рефлексивности ();

• симметричности (из следует);

• антитранзитивности .

Для этого отношения, в отличие от эквивалентности, транзитивность не обязательна, и значит, эквивалентность есть частный случай толерантности.

Отношение толерантности представляет собой формальное представление интуитивных понятий о сходстве и неразличимости. Каждый объект неразличим сам с собой (рефлексивность), а сходство двух объектов не зависит от того, в каком порядке они сравниваются (симметричность). В то же время, если один объект сходен с другим, а другой сходен с третьим, то это не означает, что все они обязательно сходны между собой, т.е. свойство транзитивности может не выполняться.

Пример.

Отношение «расстояние между двумя точками не превышает некоторого заданного числа » является отношением толерантности. Это значит, что толерантны любые две точки, расстояния между которыми не превышает.

На множестве кортежей (векторов) толерантность можно задать различными способами, например, обусловить наличие в паре кортежей хотя бы одной общей компоненты. Компонентами кортежа могут быть любые объекты. Если они принимают целочисленное значение от 0 до, то кортеж можно рассматривать как-разрядное число, записанное в позиционной системе счисления с основанием

Пример. Кортеж соответствует десятичному числу 70492. количество всех таких кортежей, очевидно, равно.

При имеем двоичный кортеж, его компоненты принимают значения 0 или 1. Для каждогосуществует только один не толерантный ему кортеж.

Пример. Двоичный кортеж можно трактовать также как содержимое -разрядного регистра вычислительной машины. Состояние машины определяется содержимым всех его регистров, т.е. множеством двоичных кортежей. Если два состояния машины различаются содержимым некоторого ограниченного числа регистров, то говорят, что эти состояния толерантны, а машину называют толерантным автоматом.

4.3 Контрольные вопросы и задания

1. Перечислите основные свойства отношений.

2. Что такое рефлексивность отношения?

3. Какое отношение является антирефлексивным?

4. Какое отношение является симметричным?

5. Какое отношение является асимметричным?

6. Какое отношение является антисимметричным?

7. Какое отношение является транзитивным?

8. Какое отношение в множестве называется отношением эквивалентности?

9. Какое отношение в множестве называется отношением нестрогого порядка?

10. Какое отношение в множестве называется отношением строгого порядка?

11. Какое отношение называется функциональным?

Лекция 5 Функциональные отношения. Элементы реляционной алгебры

5.1 Функциональные отношения

Определение

Отношение называетсяфункциональным, если его элементы (упорядоченные пары ) имеют различные первые координаты, т.е. каждомулибо соответствует только один элемент, такой, что, либо такого элементавообще не существует.

Матрица функционального отношения содержит в каждой строке не более одного единичного элемента, а его граф характеризуется тем, что из каждой вершины может выходить только одна дуга (считая и петли). Элементам , не входящим в область определения функционального отношения, соответствует нулевой столбец в матрице и изолированная вершина в графе функционального отношения.

Пример. Пусть заданы множества и. Отношениеявляется функциональным. В матрице данного отношения четвертый столбец нулевой, а его граф содержит изолированную вершину.

Для множеств иотношение, имея различные первые координаты, также является функциональным.

Всякое функциональное отношение можно рассматривать как функцию.

Определение

Бинарное отношение называетсяфункцией, или отображением, из множества в множество, если область определения функции, область значений функциии из,следует, что. Функцияиз множествав множествообозначаетсяили.

Если вместо выполняется, тоназываетсячастичной функцией.

Определение

Если множество , то черезобозначается образ множества. Множествоназываетсяобразом или областью значений отображения и обозначается. Если множество, то множествоназываетсяпрообразом множества относительно отображения .

Однако следует различать функцию как множество упорядоченных пар (отношение) и значение функциикак вторую координату одной из таких пар.

Для всякого функционального отношения можно определить связанную с этим отношением функцию, но симметричное к нему отношениеможет не быть функцией.

Пример. Пусть задано функциональное отношение .

Так, отношение , обратное рассмотренному отношению, не является функцией, так как имеют одинаковые первые координаты.

Существуют следующие основные типы отображений (функций):

• сюръекция (функция, сюръективное отображение на);

• инъекция (инъективная функция, инъективное отображение на);

• биекция (биективная функция, биективное отображение на, взаимнооднозначное соответствие).

Определение

Функция называетсясюръективной функцией (сюръективным отображением), если . Для сюръективной функции для любогосуществуеттакой, что.

На графе, представляющем сюръективное отображение , из любой вершинывыходит в точности одна дуга, а в любую вершину, представляющую элемент множества, входит не менее одной дуги.

Пример.

Сюръективное отображение на, заданное в виде графа, представлено на рис. 5.1.

Рисунок 5.1  Сюръективное отображение на, представленное в виде графа

Определение

Функция называетсяинъективной функцией (инъективным отображением), если для любых элементов изследует(отношениеявляетсячастичной функцией).

На графе, представляющем инъективное отображение , из любой вершинывыходит в точности одна дуга, а в любую вершину, представляющую элемент множества, входит не более одной дуги.

Пример.

Инъективное отображение, заданное в виде графа, представлено на рис. 5.2.

Рисунок 5.2  Инъективное отображение на, представленное в виде графа

Определение

Функция называетсябиективной функцией (биективным отображением), если она одновременно сюръективна и инъективна.

Биективное отображение осуществляетвзаимнооднозначное отображение между множествами и, поэтому,.

Свойство биективности обеспечивает существование обратного отображения. Это означает, что если биективно, то существует обратное отображение, причем.

На графе, представляющем биективное отображение конечных множеств, их любой вершинывыходит в точности одна дуга, а в любую вершину, представляющую элемент множества, входит одна и только одна дуга.

Пример. Биективное отображение на, заданное в виде графа, представлено на рис. 5.3.

Рисунок 5.3  Биективное отображение на, представленное в виде графа

Пример. Дадим характеристику свойств соответствий, представленных на рис. 5.4:

Рисунок 5.4  Соответствия

а  соответствие всюду определено, не сюръективно, не инъективно, функционально, не является биективным,является отображением, так как оно всюду определено и функционально;

б  соответствие всюду определено, сюръективно, не функционально;

в  соответствие является биективным, а значит функцией и отображением;

г  частичное соответствие, сюръективно, инъективно, функционально (однозначно), но не является отображением.

Пример.

Различные виды кодирования (кодирование букв азбукой Морзе, представления чисел в различных системах счисления, секретные шифры, входящие и исходящие номера в деловой переписке и т.д.) являются соответствиями между кодируемыми объектами и присваиваемыми им кодами. Эти соответствия, как правило, обладают всеми свойствами взаимно-однозначного соответствия, кроме, возможно, одного  сюръективности. Единственность образа и прообраза в кодировании гарантирует однозначность шифровки и дешифровки. Отсутствие сюръективности означает, что не каждый код имеет смысл. Например, кодирование телефонов шестизначными номерами не сюръективно, поскольку некоторые номера не соответствуют никаким телефонам. Для кодирующей функции, которая каждому объекту из своей области значений ставит в соответствие некоторый код, обратной будет декодирующая функция, которая каждому коду ставит в соответствие закодированный этим кодом объект. Если кодирующая функция не сюръективна, то декодирующая функция не всюду определена.

5.2 Элементы реляционной алгебры

Алгебра отношений находит широкое применение при формализации реальных объектов. Рассмотрим специфику её использования при создании элементов внутримашинного информационного обеспечения  разработке информационной базы данных. Алгебра отношений в данном случае носит название реляционной алгебры (relation  отношение) и применяется для работы с реляционной моделью данных. Реляционная модель данных с математической точки зрения является табличным представлением данных, которое легко формулируется в терминах отношений.

Рассмотрим отношение , заданное на множествах, которое при работе с реляционными базами данных задается на конечных множествах и поэтому является конечным. Основой построения реляционной базы данных (реляционной модели данных) является отношение, представленное в виде двумерной таблицы (с именем) размером, где мощность отношения, а  его арность. Каждый столбец данной таблицы соответствует домену (или атрибуту, соответствующему части домена), строка  кортежу значений атрибутов, находящихся в отношении (или записи отношения ).

Пример. Пусть имеется информация о студентах университета, представленная в следующей таблице.

Фамилия	Инициалы	Группа
Алексеев	И.А.	ПО-01
Андреева	О.П.	ПМ-01
Баранов	Н.П.	ПМ-01
Быкова	Н.А.	ПО-01
Волков	В.В	ПМ-01

Эта информация представляет собой некоторое отношение , заданное на трех множествах: множестве фамилий, множестве инициалов и множестве групп. Отношениеможно записать списком его элементов, т.е. {(Алексеев, И.А., ПО-01), (Андреева, О.П., ПМ-01), (Баранов, Н.П., ПМ-01), (Быкова, Н.А., ПО-01), (Волков, В.В, ПМ-01)}. Отношению присваивают имя, например, СТУДЕНТ_1.

Рассмотрим терминологию, применяемую при построении реляционной модели данных.

Определение.

Если , то элемент, соответствующий строке таблицы, называетсякортежем (записью).

Пример.

Кортежами являются такие элементы отношения , как (Алексеев, И.А., ПО-01), (Андреева, О.П., ПМ-01), (Баранов, Н.П., ПМ-01) и т.п.

Определение.

Множества или области данных , которые входят в произведение, т.е. на которых определено отношение, называютсядоменами.

Пример.

Доменами отношения , представленными на рис. 5.5, являются: множество фамилий, множество инициалов и множество групп, соответствующие столбцам таблицы.

Рисунок 5.5  Домены отношения

Определение.

Наименования столбцов таблицы называют атрибутами.

Пример.

Атрибутами отношения СТУДЕНТ_1 являются: фамилия, инициалы, группа.

Представим это отношение на рис. 5.6.

Рисунок 5.6 Отношение СТУДЕНТ_1

Определение. Схемой отношения является список атрибутов.

Пример.

Схемой отношения СТУДЕНТ_1 является список (Фамилия, Инициалы, Группа).

Для изменения содержимого таких таблиц (реляционных таблиц) в базах данных используются простые следующие операции по заполнению таблицы: добавление, удаление кортежей, изменение значения атрибутов.

Основная идея реляционной алгебры заключается в следующем. Поскольку отношения являются множествами, то средства манипулирования отношениями могут базироваться на таких традиционных теоретико-множественных операциях, как объединение, пересечение, разность, декартово произведение, дополненных некоторыми специальными операциями. Следовательно, носитель реляционной алгебры представляет собой множество отношений , сигнатуракроме операцийобъединения, пересечения, разности, декартова произведения включает специальные операции над отношениями: ограничение отношений (выбор), проекцию отношений, соединение отношений, деление отношений.

В соответствии с потребностями практики вводятся и некоторые другие операции.

Рассмотрим теоретико-множественные операции, применяемые для преобразования отношений в базе данных, используя термины реляционной алгебры.

Определение. Отношения, к которым применяется операция, будем называть отношениями-операндами.

К теоретико-множественным операциям реляционной алгебры относятся:

• объединение отношений;

• пересечение отношений;

• разность отношений;

• прямое (декартово) произведение отношений.

Эти операции имеют смысл для отношений, определенных на одинаковых доменах.

Определение. Объединение отношений (). При выполнении операции объединения двух отношений получаем отношение, включающее все кортежи, входящие хотя бы в одно из отношений-операндов.

Пример. Рассмотрим отношения СТУДЕНТ_1 и СТУДЕНТ_2.

СТУДЕНТ_1

Фамилия	Инициалы	Группа
Алексеев	И.А.	КН-01
Андреева	О.П.	ПМ-01
Баранов	Н.П.	ПМ-01
Быкова	Н.А.	КН-01
Волков	В.В	ПМ-01

СТУДЕНТ_2

Фамилия	Инициалы	Группа
Алексеев	И.А.	КН-01
Быкова	Н.А.	КН-01
Дроздов	И.К.	КН-01
Зайцев	О.Н.	ПМ-01
Кузнецова	Е.В	КН-01

Применим операцию объединения к отношениям СТУДЕНТ_1 и СТУДЕНТ_2.

В результате получим следующее отношение (ВСЕ_СТУДЕНТЫ).

ВСЕ_СТУДЕНТЫ=СТУДЕНТ_1СТУДЕНТ_2

Фамилия	Инициалы	Группа
Алексеев	И.А.	КН-01
Андреева	О.П.	ПМ-01
Баранов	Н.П.	ПМ-01
Быкова	Н.А.	КН-01
Волков	В.В	ПМ-01
Дроздов	И.К.	КН-01
Зайцев	О.Н.	ПМ-01
Кузнецова	Е.В	КН-01

Определение.

Пересечение отношений (). При выполнении операции пересечения двух отношений получаем отношение, включающее только те кортежи, которые входят в оба отношения-операнда.

Пример.

Рассмотрим отношения СТУДЕНТ_1 и СТУДЕНТ_2 (из предыдущего примера). Применим операцию пересечения к отношениям СТУДЕНТ_1 и СТУДЕНТ_2.

В результате получим следующее отношение (СТУДЕНТ_1СТУДЕНТ_2).

СТУДЕНТ_1СТУДЕНТ_2

Фамилия	Инициалы	Группа
Алексеев	И.А.	КН-01
Быкова	Н.А.	КН-01

Определение.

Разность отношений (\). Отношение, являющееся разностью двух отношений, включает все кортежи, входящие в отношение-первый операнд, такие, что ни один из них не входит в отношение, являющееся вторым операндом.

Пример.

Рассмотрим отношения СТУДЕНТ_1 и СТУДЕНТ_2 (из предыдущего примера). Применим операцию (\) к отношениям СТУДЕНТ_1 и СТУДЕНТ_2.

В результате получим следующее отношение (СТУДЕНТ_1\СТУДЕНТ_2).

СТУДЕНТ_1\СТУДЕНТ_2

Фамилия	Инициалы	Группа
Андреева	О.П.	ПМ-01
Баранов	Н.П.	ПМ-01
Волков	В.В	ПМ-01

Определение.

Прямое (декартово) произведение отношений (). При выполнении прямого произведения двух отношений получаем отношение, множество кортежей которого является декартовым произведением множеств кортежей первого и второго операндов.

Пример.

Рассмотрим отношение СТУДЕНТ_1 (из предыдущих примеров) и КУРС.

КУРС

Уч. год	Курс
2009-2010	1
2010-2011	2

Выполним прямое произведение отношения СТУДЕНТ_1 и КУРС.

В результате получим следующее отношение (СТУДЕНТ_1КУРС).

СТУДЕНТ_1КУРС

Фамилия	Инициалы	Группа	Уч. год	Курс
Алексеев	И.А.	КН-01	2009-2010	1
Алексеев	И.А.	КН-01	2010-2011	2
Андреева	О.П.	ПМ-01	2009-2010	1
Андреева	О.П.	ПМ-01	2010-2011	2
Баранов	Н.П.	ПМ-01	2009-2010	1
Баранов	Н.П.	ПМ-01	2010-2011	2
Быкова	Н.А.	КН-01	2009-2010	1
Быкова	Н.А.	КН-01	2010-2011	2
Волков	В.В	ПМ-01	2009-2010	1
Волков	В.В	ПМ-01	2010-2011	2

Далее рассмотрим специальные операции реляционной алгебры, применяемые в базах данных. К таким операциям следует отнести:

• ограничение отношений;

• проекция отношений;

• естественное соединение отношений;

• деление отношений.

Определение.

Ограничение отношений (). Результатом ограничения отношения по некоторому атрибуту или атрибутамявляется отношение, состоящее в точности из тех кортежей, которые удовлетворяют условию.

Пример.

Выполним ограничение отношения ВСЕ СТУДЕНТЫ по атрибуту Группа=КН-01. Результат назовем СТУДЕНТ_КН-01. В результате получим отношение (ВСЕ СТУДЕНТЫ)=СТУДЕНТ_КН-01, содержащее только кортежи, в которых значение атрибута Группа равняется КН-01.

СТУДЕНТ_КН-01

Фамилия	Инициалы	Группа
Алексеев	И.А.	КН-01
Быкова	Н.А.	КН-01
Дроздов	И.К.	КН-01
Кузнецова	Е.В	КН-01

Определение.

Проекция отношения (). При выполнении проекции отношения на заданный набор его атрибутов отношение-результат получается путем удаления из отношения-операнда атрибутов, не указанных в заданном наборе.

Схематически выполнение операции представлено на рис. 5.7.

Рисунок 5.7  Схема выполнения операции проекции по

Пример. Выполним проекцию отношения СТУДЕНТ_1_КУРС по атрибутам Группа, Уч. год, Курс.

( СТУДЕНТ_1_КУРС)

Группа	Уч. год	Курс
КН-01	2009-2010	1
КН-01	2010-2011	2
ПМ-01	2009-2010	1
ПМ-01	2010-2011	2

Определение. Естественное соединение отношений (І><I). При естественном соединении двух отношений образуется результирующее отношение, кортежи которого являются соединением кортежей первого и второго отношений, если значение общих атрибутов совпадает.

Схематически выполнение операции І><I представлено на рис. 5.8.

Рисунок 5.8  Схема выполнения операции естественного соединения отношений

Пример. Пусть задано отношение НОМЕР

НОМЕР

Фамилия	Инициалы	Зачетка №	Студ. №
Алексеев	И.А.	11197	784567
Андреева	О.П.	11215	784565
Баранов	Н.П.	11213	784598
Быкова	Н.А.	11216	784588
Волков	В.В	11217	784599
Дроздов	И.К.	11193	784611
Зайцев	О.Н.	11191	784601
Кузнецова	Е.В	11195	785587

Выполним естественное соединение отношений СТУДЕНТ_КН-01 и НОМЕР.

СТУДЕНТ_КН-01 І><I НОМЕР

Фамилия	Инициалы	Группа	Зачетка №	Студ. №
Алексеев	И.А.	КН-01	11197	784567
Быкова	Н.А.	КН-01	11216	784588
Дроздов	И.К.	КН-01	11193	784611
Кузнецова	Е.В	КН-01	11195	785587

Определение.

Деление отношений (). Операция деления отношений осуществляется следующим образом. Отношение-делитель должно иметь набор атрибутов, включенный в набор атрибутов делимого. Результирующее отношение содержит те атрибуты делимого, которые не присутствуют в делителе. Значения этих атрибутов берутся из тех кортежей делимого, которые включают в себя кортежи делителя.

Схематически выполнение операции представлено на рис. 5.9.

Рисунок 5.9  Схема выполнения операции деления отношений ()

Пример.

Выполним проекцию отношения СТУДЕНТ_КН-01 по атрибутам Фамилия, Инициалы, т.е. ФАМИЛИЯ СТУДЕНТ_КН_01=(СТУДЕНТ_КН-01).

ФАМИЛИЯ СТУДЕНТ_КН_01

Фамилия	Инициалы
Алексеев	И.А.
Быкова	Н.А.
Дроздов	И.К.
Кузнецова	Е.В

Затем произведем деление отношения НОМЕР на отношение ФАМИЛИЯ СТУДЕНТ_КН_01.

В результате деления получим таблицу номеров студентов группы КН-01.

НОМЕРФАМИЛИЯ СТУДЕНТ_КН_01

Зачетка №	Студ. №
11197	784567
11216	784588
11193	784611
11195	785587

Кроме рассмотренных операций реляционной алгебры, в набор операций базы данных обычно включается операция присваивания, позволяющая сохранить результаты вычисления алгебраических выражений, операция переименования атрибутов, дающая возможность корректно сформировать заголовок (схему) результирующего отношения и другие полезные операции.

5.3 Контрольные вопросы и задания

1. Какое функциональное отношение называется всюду определенным?

2. Как выглядит матрица функционального отношения?

3. Какое функциональное отношение называют отображением множества в?

4. Что такое сюръекция?

5. Что такое инъекция?

6. Что такое биекция?

7. Какое отображение называется взаимно однозначным?

8. Что называется образом элемента?

9. Что такое прообраз элемента?

10. Перечислите основные свойства отображений.

11. Что представляет собой реляционный метод построения баз данных?

12. Что называется кортежем, атрибутом, доменом?

13. Перечислите теоретико-множественные операции, применяемые при работе с реляционными базами данных. Объясните принцип их выполнения.

14. Перечислите специальные реляционные операции. Объясните принцип выполнения каждой из них.

Лекция 6. Двузначная логика. Булевы функции. Основные понятия

6.1 Двузначная логика

В данном разделе курса «Дискретная математика» рассматриваются базовые элементы аппарата двузначной логики (который был разработан Д. Булем в середине ХІХ века) − булевы функции и преобразования над ними.

Данные функции являются наиболее простым и в то же время важнейшим классом функций, которые используются для описания работы ЭВМ, конечных автоматов, вычислительных систем.

Применение булевых функций легко распространяется на объекты самой общей природы, лишь бы только они характеризовались конечным числом состояний.

Двузначная логика (булева алгебра) имеет дело с такими объектами, которые принимают одно из двух возможных значений (высокое или низкое напряжение, наличие или отсутствие заданного признака у объекта, истинное или ложное высказывание и т.п.).

Понятия, методы и средства данного типа логики лежит в основе современных компьютерных технологий.

6.2 Булевы переменные и функции

Рассмотрим основные понятия и определения алгебры логики.

Пусть задано двухэлементное множество и двоичные переменные, принимающие значения из. Элементычасто обозначают 0 и 1, однако они не являются числами в обычном смысле. Наиболее распространенная интерпретация двоичных переменных – логическая: «нет» – «да», «истинно» (и) – «ложно» (или), «false» – «true». Будем считать, что , рассматривая 0 и 1 как формальные символы, не имеющие арифметического смысла.

Определение.

Переменные, которые могут принимать значения только из множества , называютсябулевыми или логическими переменными. Элемент 1 называется единичным элементом, или единицей; элемент 0 называется нулевым элементом, или нулем. Сами значения 0 и 1 называются булевыми константами.

Пример.

Булевыми переменными, которые способны принимать лишь два различных значения, характеризуются объекты с двумя возможными состояниями (наличие или отсутствие у объекта определенного признака, низкое или высокое напряжение, истинное или ложное высказывание).

Пример.

В языках программирования для работы с такими переменными, как правило, вводится специальный логический тип (например, в языках Pascal и Java  boolean, в  bool). Переменная этого типа принимает два значения «false» и «true».

Отношения между булевыми переменными представляются булевыми функциями, которые подобно числовым функциям могут зависеть от одной, двух и, вообще, переменных (аргументов).

Определение.

Функция вида , аргументыи значениякоторой принадлежат множеству, называется-местнойбулевой (переключательной, логической) функцией.

Важнейшая особенность булевых функций состоит в том, что они, как и их аргументы, принимают свои значения из двухэлементного множества , т.е. характеризуются одним из двух возможных состояний.

Пример.

В вычислительной технике булевы функции применяются для описания алгоритмов, средств вычислительной техники – дискретных устройств. Дискретные устройства предназначаются для преобразования дискретной информации, разлагающейся на элементарные единицы – биты. Биты в устройствах реализуются сигналами, которые описываются двоичными переменными – булевыми.

Определение.

Совокупность конкретных значений аргументов булевой функции называется кортежем, двоичным словом (-словом) или булевым набором длины и обозначается как . Для булевой функцииконкретное (индивидуальное) значение булевого набораназывается такжеинтерпретацией булевой функции f.

Пример. Для булевой функции кортежами являются следующие совокупности конкретных значений аргументов:,,,; для булевой функциикортежами являются:,,,и т.д.

6.3 Область определения и область значений булевой функции

Определение.

Множество всех двоичных слов, обозначаемое как , называетсяn-мерным булевым кубом и содержит элементов-слов, т.е..

Пример.

В множество двоичных слов для булевой функции входитслова: (0) и (1); в множество двоичных слов для булевой функциивходитслов:,,,,,,,.

Определение.

Областью определения булевой функции от -переменных служит множество слов длины, которые представляют собой всевозможные наборы издвоичных цифр и их общее количество равно.

Определение.

Функция, зависящая от аргументов, являетсяполностью определенной, если указаны её значения для всех наборов (кортежей, слов) значений элементов.

Пример.

Булева функция от двух элементов является полностью определенной, если указаны её значения для каждого из четырех возможных наборов (), функция трех аргументов – на 8 () наборах также будет полностью определенной.

Теорема 6.1

Число всех функций, зависящих от переменных, равно.

Действительно, булева функция аргументов определена нанаборах, на которых она может принимать «0» или «1» из общего количества. Поэтому в соответствие каждой булевой функции можно поставить-разрядное двоичное число. Но количество различных-разрядных чисел равно, а следовательно и количество различных булевых функций равно.

Пример. От двух аргументов существует 16 булевых функций, т.е.; от трех – 256 (), от четырех – 65536 функций ().

6.4 Способы задания булевых функций

Существует четыре способа задания булевой функции:

• вербальный (словесный);

• табличный (с помощью таблицы истинности);

• порядковым номером, который имеет функция;

• аналитический (в виде формулы).

Задание булевых функций при помощи таблиц. Булевы функции можно задавать с помощью таблиц, подобных таблицам сложения и умножения одноразрядных чисел. В левой части такой таблицы перечисляются все наборов значений переменных (булевых наборов длины), а в правой части − значения функций на этих наборах. Этот способ задания универсален, т.е. пригоден для любой функции, однако громоздок, поэтому применяется для задания функции небольшого числа переменных.

Определение.

Таблицы, в которых каждой интерпретации (то есть набору аргументов) функции поставлено в соответствие её значение, называются таблицами истинности (соответствия) булевой функции.

В таблице истинности каждой переменной и значению самой функциисоответствует по одному столбцу, а каждой интерпретации по одной строке. Интерпретации расположены в определенном порядке − лексикографическом, который совпадает с порядком возрастания наборов, рассматриваемых как двоичные числа.

Пример.

Таблица истинности функции может иметь следующий вид (табл. 6.1).

Таблица 6.1 – Пример таблицы истинности функции

0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	1
1	0	0	1
1	0	1	1
1	1	0	0
1	1	1	0

В столбцах 1, 2, 3 даны все возможные кортежи значений трех аргументов, т.е. сочетание нулевых и единичных значений трех аргументов. В столбце 4 – значения функции .

Рассмотрим булевы функции, которые зависят от одной и двух переменных.

Булевы функции, которые зависят от одной переменной, приведены в табл. 6.2 (их количество равно ).

Таблица 6.2  Таблица истинности для булевых функций одной переменной

0	0	0	1	1
1	0	1	0	1

Две функции ипредставляют собой функции-константы:

• является абсолютно ложной (константа нуля);

• является абсолютно истинной (константа единицы).

Функция (функция повторения аргумента) повторяет значения переменнойи поэтому просто совпадает с ней. Функция, называемаяотрицанием или инверсией (читается «не»), является единственной нетривиальной функцией. Она равна 1, когда аргумент принимает значение 0, и равна 0 при аргументе 1.

Всевозможные булевы функции двух переменных представлены в табл. 6.3 (их количество равно).

Таблица 6.3  Таблица истинности для булевых функций двух переменных

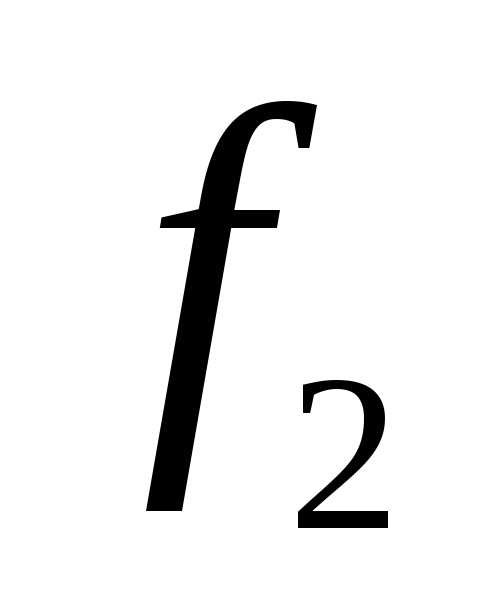
0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1

В табл. 6.4 приведена характеристика булевых функций двух переменных.

Таблица 6.4  Характеристика булевых функций двух переменных

Функ-ция	Обозначения (другие обозначения)	Названия	Чтение
	0	Константа 0 (тождественный нуль, всегда ложно)	Константа 0 (Любое 0)
	() (AND, И)	Конъюнкция (произведение, пересечение, логическое «и»)	и (и и). Истинна тогда, когда истинны обе переменные
	() (>)	Отрицание импликации (запрет)	, но не
		Повторение (утверждение) первого аргумента	Как
	()	Отрицание обратной импликации	Не , но
		Повторение второго аргумента	Как
	()	Сумма по модулю 2 (неравнозначность, антиэквивалетность)	не как (или или). Истинна, когда истинны или , илив отдельности
	() (OR, ИЛИ)	Дизъюнкция (логическая сумма, логическое «или»)	или (или хотя бы). Истинна тогда, когда истинны или , или, или обе переменные
	()	Стрелка Пирса (функция Вебба, отрицание дизъюнкции)	Не и не. Истинна только тогда, когда иложны
	() (Eqv)	Эквиваленция (равнозначность, эквивалентность)	как (, если, и только если)
	()	Отрицание (инверсия) второго аргумента	Не
	()	Обратная импликация (обратное разделение с запретом)	Если , то (или не)
	()	Отрицание (инверсия) первого аргумента	Не
	() (Imp)	Импликация (следование, селекция)	Если , то (не или). Ложна тогда и только тогда, когда истинна иложна
	()	Штрих Шеффера (отрицание конъюнкции, несовместимость, логическое «не-и»)	Не или не. Ложна только тогда, когда иистинны
	1	Константа 1 (тождественная единица, всегда истинно)	Константа 1 (Любое 1)

Шесть из приведенных функций не зависят от или(или от обоих вместе). Это две константы (и), повторения (,) и отрицания (и), являющиеся функциями одной переменной (или.) Из остальных десяти функций две (и) отличаются от соответствующих им (и) лишь порядком расположения элементов и поэтому не являются самостоятельными. Поэтому из 16 функций двух переменных только восемь являются оригинальными ().

В математической логике часто употребляются так называемые элементарные функции, которые играют такую же важную роль, как, например, илив математическом анализе. Элементарные логические функции –6это одноместные и двухместные логические функции.

Примеры элементарных функций одной переменной приведены в табл. 6.2.

Примеры элементарных функций двух переменных представлены в табл. 6.3 и 6.4, это: отрицание (); дизъюнкция; конъюнкция; импликация; эквивалентность; сумма по модулю 2; штрих Шеффера; стрелка Пирса.

Булевы функции можно рассматривать как логические операции над величинами, принимающими два значения – 0 и 1. Основными в двузначной логике являются три функции:

• отрицание (функция , принимающая значения 1, когда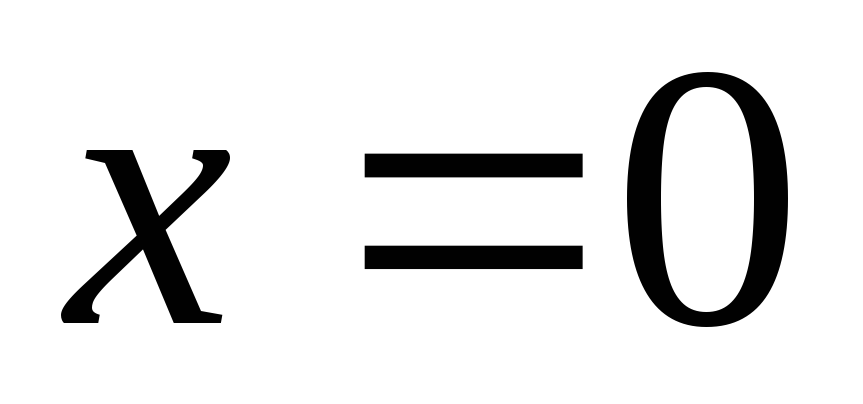, и значение 0, когда);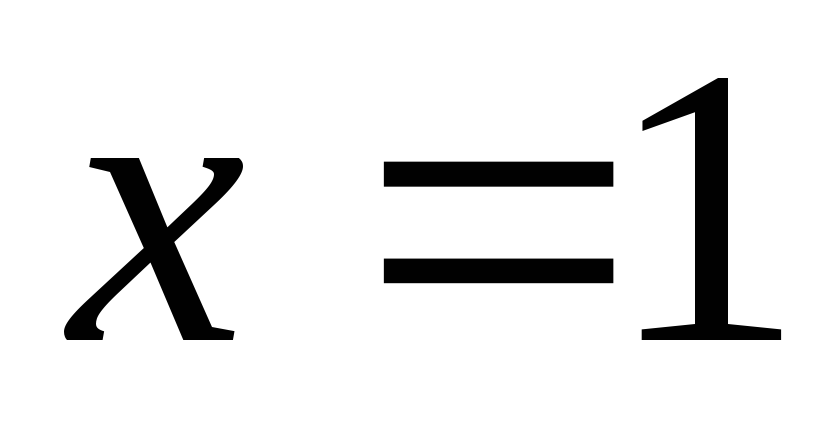

• дизъюнкция (функция , принимающая значение 0 тогда и только тогда, когда оба аргумента имеют значение 0);

• конъюнкция (функция 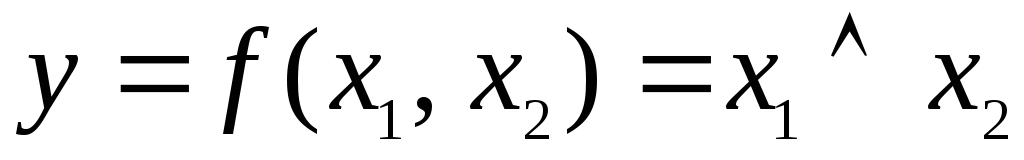, принимающая значение 1 тогда и только тогда, когда оба аргумента имеют значение 1).

Задание булевой функции порядковым номером. Каждой функции присваивается порядковый номер в виде натурального числа, двоичный код которого представляет собой столбец значений функции в таблице истинности. Младшим разрядом считается самая нижняя строка (значение функции на интерпретации , а старшим самая верхняя (значение функции на интерпретации ). Указанный порядковый номер функции, как двоичный, так и десятичный, полностью определяет булеву функцию.

Часто для упрощения записи булевой функции вместо полного перечисления интерпретаций используют только двоичные значения наборов, для которых функция принимает единичные значения. Такую форму записи называют числовой.

Пример.

Найдем порядковый номер функции , которая задана таблицей истинности (см. табл. 6.1). Для этого переведем двоичное числов десятичную систему счисления:

Кортеж значений аргументов (интерпретацию) также можно рассматривать как запись целого положительного числа в двоичной системе счисления. Первая интерпретация в таблице истинности называется нулевой, последняя – единичной (номер интерпретации , где– количество аргументов функции).

Определение.

Десятичный эквивалент двоичного представления интерпретации называется номером интерпретации (кортежа).

Пример.

Шестой интерпретацией является , т.е..

Пример.

Пусть функция принимает единичные значения на интерпретациях 1, 4, 7. Тогда, используя числовую форму записи, функция будет иметь вид:, что означает, что функция принимает единичные значения на наборах 1, 4 и 7.

6.5 Реализация булевых функций формулами

Булевы функции могут быть заданы аналитически, т.е. формулами (аналитическими выражениями).

Определение.

Формула – это выражение, содержащее булевы функции и их суперпозиции.

Пример.

Формулы булевой алгебры можно представить следующим образом:

; [], .

Определение.

Суперпозицией называется прием получения новых функций путем подстановки значений одних функций вместо значений аргументов других функций.

Пример.

Рассмотрим формулу, задающую функцию следующим образом. Эта формула содержит функции: отрицание,  конъюнкцию,  дизъюнкцию. Данную формулу можно представить в виде суперпозиции указанных функций следующим образом:

Как и в элементарной алгебре, в алгебре логики можно строить формулы, исходя из элементарных функций.

При образовании (построении) формул используются знаки (символы) трех категорий:

1. символы первой категории обозначают переменные: ;

2. символы логических операций и т.д.;

3. пары символов (), [], {}.

Если в формуле отсутствуют скобки, то операции выполняются в следующей последовательности: отрицание, конъюнкция, дизъюнкция, импликация, и эквивалентность: .

Определение.

Запись формул, при которой знаки функций стоят между аргументами, называют инфиксной (в дальнейшем будем пользоваться такой формой записи).

Формула каждому набору значений аргумента ставит в соответствие значение функции и, следовательно, может служить, наряду с таблицей, способом задания и вычисления функций. По формуле можно восстановить таблицу функций.

Определение.

О формуле, задающей функцию, говорят также, что она реализует или представляет эту функцию.

В отличие от табличного задания представление булевой функции формулой не единственно.

Определение.

Формулы, представляющие одну и ту же функцию, называются эквивалентными или равносильными.

Две функции (как и определяющие их формулы) считаются равносильными, если при любых значениях аргументов эти функции (формулы) принимают одинаковые значения. Равносильные функции соединяются знаком равенства.

Пример. Равносильные функции или.

Пример.

Важнейшие примеры равносильных функций: равносильно;равносильно;равносильно;равносильно;равносильно;равносильно;равносильно;равносильно.

Чтобы выяснить, являются ли данные формулы эквивалентными (равносильными), существует, по крайней мере, два метода:

• стандартный метод (построение таблицы функции);

• метод эквивалентных преобразований формул.

6.6 Принцип двойственности

Одним из способов получения тождеств в булевой алгебре является способ, основанный на принципе двойственности.

Определение.

Функция называетсядвойственной к функции , если.

Для любой функции двойственная ей функция определяется однозначно.

Отношение двойственности симметрично.

Определение.

Функция, двойственная сама себе, т.е. , называетсясамодвойственной.

Самодвойственные функции принимают противоположные значения на любых двух противоположных наборах. Если в таблице истинности функции наборы, как обычно, следуют в порядке их номеров, то противоположные друг другу наборы располагаются симметрично относительно середины их расположение. Это значит, что строка значений самодвойственной функции должна быть антисимметричной относительно своей середины.

Пример.

а) двойственна.

б) двойственна.

Таблица двойственности функции получается из таблицы для функции инвертированием (т.е. заменой 0 на 1 и 1 на 0) значений функции и заменой порядка следования инвертированных значений функции на противоположный (переворачиванием столбца инвертированных значений функции).

Пример.

Найдем функцию , двойственную заданной, при помощи таблицы истинности. Результат представим в табл. 6.5.

Таблица 6.5  Таблица истинности и двойственной функции

0	0
0	1
1	0
1	1

Рассмотрим таблицу истинности самодвойственной функции (табл. 6.6).

Таблица 6.6  Самодвойственная функция, представленная таблицей истинности

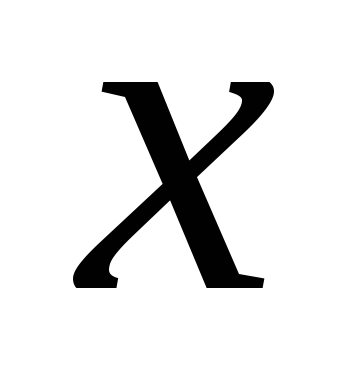
0	0
0	1
1	0
1	1

Определение.

Принцип двойственности указывает правило получения двойственных формул в булевой алгебре: «Для того чтобы получить двойственную формулу булевой алгебры, необходимо заменить в ней все конъюнкции на дизъюнкции, дизъюнкции на конъюнкции, 0 на 1, 1 на 0 и использовать скобки, где необходимо, чтобы порядок выполнения операций остался прежним».

Пример.

Найти функцию, двойственную функции .

Используя правило получения двойственных функций, получим двойственную функцию .

Определение.

Если функции равны, то и двойственные им функции также равны, т.е., если , то.

Принцип двойственности позволяет почти в два раза сократить усилия на вывод тождеств при рассмотрении свойств элементарных функций.

6.7 Булевы алгебры. Законы и тождества булевой алгебры

Определение.

Алгебраическая структура , гдеи операцияесть конъюнкция,есть дизъюнкция(таблица 3.4), «» есть отрицание(таблица 3.2), называетсядвухэлементной булевой алгеброй.

Определение.

Алгеброй логики называется двухэлементная булева алгебра , где носитель алгебры, и в которой множество операций дополнено двумя бинарными операциями: импликациейи эквивалентностью(см. таблицу 3.4).

На основе определения основных операций (отрицание, дизъюнкция, конъюнкция) нетрудно убедиться в справедливости следующих законов (свойств) булевой алгебры.

Рассмотрим основные законы (свойства) булевой алгебры.

Закон коммутативности (переместительный закон)

;

.

Пример.

Доказать коммутативность операции дизъюнкции можно, используя таблицы истинности (табл. 6.7).

Таблица 6.7  Таблица истинности для доказательства коммутативности операции дизъюнкции

0	0	0	0
0	1	1	1
1	0	1	1
1	1	1	1

Столбцы ив таблицах истинности содержат одинаковые значения, что доказывает коммутативность операции дизъюнкции.

Найдем тождество, двойственное данному тождеству, для чего заменим все функции на двойственные им ,.

Закон ассоциативности (сочетательный закон)

;

.

Пример.

Доказать ассоциативность операции конъюнкции можно, используя таблицы истинности (табл. 6.8).

Таблица 6.8  Таблица истинности для доказательства ассоциативности операции конъюнкции

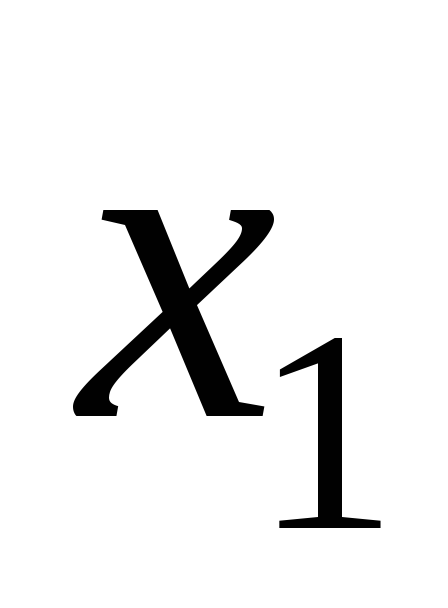
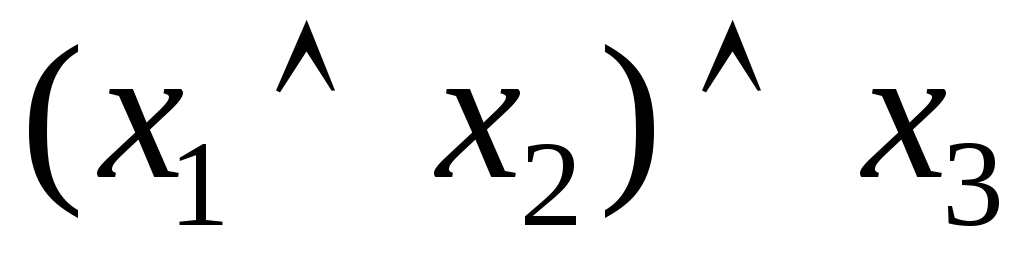
0	0	0	0	0	0	0
0	0	1	0	0	0	0
0	1	0	0	0	0	0
0	1	1	1	0	0	0
1	0	0	0	0	0	0
1	0	1	0	0	0	0
1	1	0	0	0	1	0
1	1	1	1	1	1	1

Столбцы, соответствующие левой и правой частям второго равенства, содержат одинаковые значения, что доказывает справедливость тождества .

Тождество, выражающее ассоциативность дизъюнкции, двойственно доказанному, так как может быть получено из него путем замены всех функций на двойственные им, и, следовательно, оно тоже верно.

Закон дистрибутивности (распределительный закон)

;

.

Пример.

Доказательство дистрибутивности конъюнкции относительно дизъюнкции можно провести, используя таблицы истинности (табл. 6.9).

Таблица 6.9  Дистрибутивность конъюнкции относительно дизъюнкции

0	0	0	0	0	0	0	0
0	0	1	1	0	0	0	0
0	1	0	1	0	0	0	0
0	1	1	1	0	0	0	0
1	0	0	0	0	0	0	0
1	0	1	1	1	0	1	1
1	1	0	1	1	1	0	1
1	1	1	1	1	1	1	1

Столбцы, соответствующие левой и правой частям первого равенства, содержат одинаковые значения, что и доказывает справедливость равенства . Двойственное тождество выражает дистрибутивность дизъюнкции относительно конъюнкции.

Закон идемпотентности

;

.

Пример.

Для доказательства закона идемпотентности используем таблицу истинности (табл. 6.10).

Таблица 6.10  Закон идемпотентности

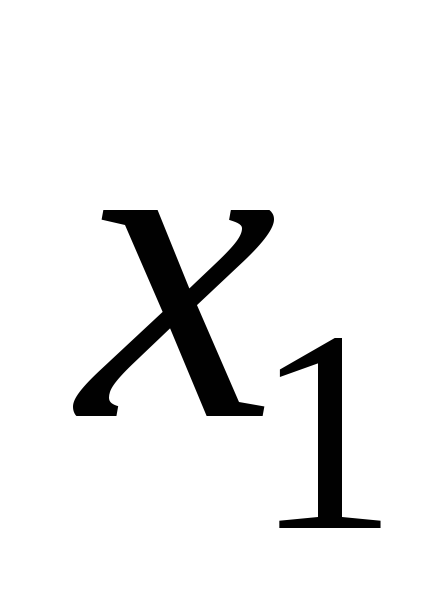
0	0	0
1	1	1

В таблице значения всех столбцов одинаковы и совпадают со значением переменной , что и доказывает оба тождества. Данные тождества являются двойственными друг другу.

Закон исключенного третьего

.

Пример.

Для доказательства закона исключенного третьего используем таблицу истинности (табл. 6.11).

Таблица 6.11  Закон исключенного третьего

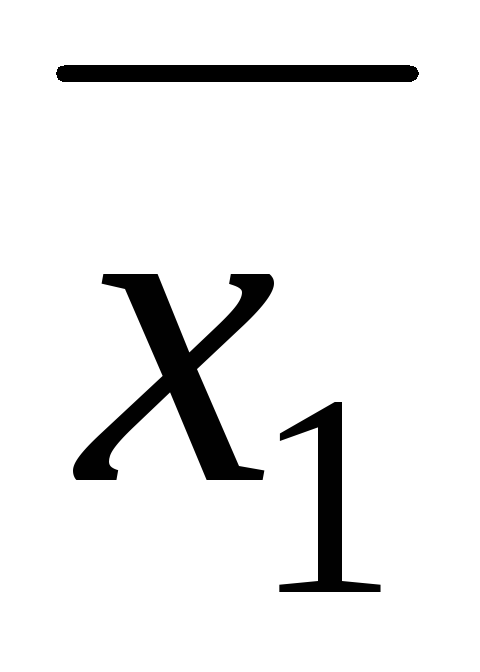
0	1	1
1	0	1

Столбец истинности, представляющий левую часть доказываемого тождества, равен константе единицы, что и требовалось доказать.

Закон противоречия

.

Пример.

Для доказательства закона противоречия используем таблицу истинности (табл. 6.12).

Таблица 6.12  Закон противоречия

0	1	0
1	0	0

Данный закон является двойственным к доказанному выше закону исключенного третьего.

Закон тождества (свойство констант)

; ;

; .

Пример. Для доказательства закона тождества (свойство констант) используем таблицу истинности (табл. 6.13).

Таблица 6.13  Таблицы истинности тождеств

0	0	0	1	0
1	1	1	1	0

Закон поглощения (элиминации)

;

.

Пример.

Докажем закон поглощения (элиминации) аналитически, используя тождества с константами и дистрибутивный закон:

;

.

Закон инволюции (двойного отрицания)

.

Пример.

Для доказательства закона инволюции (двойного отрицания) используем таблицу истинности (табл. 6.14).

Таблица 6.14  Закон двойного отрицания

0	1	0
1	0	1

Законы де Моргана

;

.

Пример.

Для доказательства закона де Моргана используем таблицу истинности (табл. 6.15).

Таблица 6.15  Доказательство закона де Моргана

0	0	0	1	1	1	1
0	1	1	0	1	0	0
1	0	1	0	0	1	0
1	1	1	0	0	0	0

Второй закон де Моргана является двойственным первому и, значит, также является верным.

6.8 Контрольные вопросы и задания

1. Какие переменные называются булевыми или логическими переменными?

2. Какая функция называется логической (булевой, переключательной)?

3. Приведите примеры задания (использования) булевых переменных в языках программирования.

4. Как называется совокупность конкретных значений аргументов булевой функции?

5. Сколько элементов-слов содержит -мерный булевый куб?

6. Что представляет собой область определения и область значений булевой функции?

7. Какая булева функция называется полностью определенной?

8. Как определить число всех булевых функций, зависящих от переменных.

9. Перечислите способы задания булевых функций.

10. Что представляет собой таблица истинности (соответствия) булевой функции. Назовите правила её построения.

11. Перечислите булевы функции от одной переменной.

12. Приведите примеры элементарных функций двух переменных.

13. Перечислите основные булевы функции от двух переменных.

14. Каким образом определяется номер булевой функции? Номер интерпретации?

15. Дайте определение формулы для задания булевой функции. Что такое суперпозиция булевых функций?

16. Какие знаки используются при образовании (построении) формул? Какой приоритет определен для операций алгебры логики?

17. Какая запись формул называется инфиксной? Приведите примеры.

18. Чем отличается табличный и формульный способ задания булевых функций? В каких случаях применяется каждый из них?

19. Какие формулы называются равносильными или эквивалентными?

20. Перечислите основные методы определения равносильности формул.

21. Дайте определение двойственной функции.

22. Дайте определение самодвойственной функции.

23. Каким образом формируется таблица истинности двойственной функции?

24. Сформулируйте принцип двойственности булевых функций.

25. Дайте определения двухэлементной булевой алгебры и алгебры логики.

26. Перечислите основные законы булевой алгебры.

27. Каким способом можно доказать законы булевой алгебры.

28. Сформулируйте и запишите тождества для законов булевой алгебры.

Лекция 7. Нормальные формы булевых функций

7.1 Нормальные формы булевых функций, основные понятия

При практическом применении теории булевых функций часто ставится задача поиска наиболее простой (в определенном смысле) формулы среди всех эквивалентных между собой формул, представляющих рассматриваемую булеву функцию.

На примере булевых функций обсудим важное понятие «нормальной формы», то есть синтаксически однозначного способа записи формулы, реализующей заданную функцию. Данный способ основан на рассмотрении представления логических функций в виде суперпозиций функций («и»),(«или»),(«не»).

Введем понятия, определяющие способ представления формул в виде дизъюнктивных и конъюнктивных нормальных форм.

Определение.

Элементарной конъюнкцией называется конъюнкция любого числа булевых переменных, взятых с отрицанием или без него, в которой каждая переменная встречается не более одного раза. Элементарной конъюнкцией, содержащей ноль переменных, будем считать константу 1.

Пример.

Элементарными конъюнкциями для функции от одной переменной могут быть ,; для функции от двух переменных ,; для функции от трех переменных ,,и т.д.

Определение.

Дизъюнктивной нормальной формой (ДНФ) называется формула, представленная в виде дизъюнкции элементарных конъюнкций.

Пример.

Если булева функция задана формулой в виде дизъюнкции элементарных конъюнкций, то функция представлена своей дизъюнктивной нормальной формой. ДНФ функции может иметь вид.

Определение.

Члены дизъюнктивной нормальной формы, представляющие собой элементарные конъюнкции букв, называютсяминтермами -го ранга.

Пример.

Элементарная конъюнкция является минтермом второго ранга; минтермом третьего ранга;  минтермом четвертого ранга и т.п.

Определение.

Конституентой единицы (минтермом -го ранга) называют булеву функцию аргументов, которая принимает значение, равное 1, только на одной интерпретации (наборе).

Пример. Конституента единицы обращается в единицу только при одном соответствующем ей наборе значений переменных, который получается, если все переменные принять равными единице, а их отрицания  нулю, например, конституенте единицы соответствует набор (0101), а конституенте единицы набор (110).

7.2 Совершенные нормальные формы булевых функций

Среди множества эквивалентных формул, представляющих выбранную булеву функцию , выделяется одна формула, которая называетсясовершенной нормальной формой функции . Она имеет регламентированную логическую структуру и однозначно определяется по функции.

Определение.

Совершенной дизъюнктивной нормальной формой (СДНФ) функции , содержащейразличных переменных, называется дизъюнктивная нормальная форма, обладающая следующими свойствами:

а) в ней нет одинаковых слагаемых;

б) ни одно слагаемое не содержит двух одинаковых множителей;

в) никакое слагаемое не содержит переменной вместе с её отрицанием;

г) в каждом слагаемом содержится в качестве множителя либо переменная , либо её отрицание, где.

Условия а), б), в), г) являются необходимыми и достаточными для того, чтобы ДНФ была СДНФ.

Определение.

Совершенной дизъюнктивной нормальной формой (СДНФ) булевой функции называется формула, представленная в виде дизъюнкции конституент единицы данной функции.

В каждом члене СДНФ представлены все переменные (либо в прямом, либо в инверсном виде).

Всякая булева функция , которая не является тождественным нулем, имеет:

• несколько ДНФ;

• одну и только одну СДНФ (количество её членов равно количеству единичных значений функции).

Определение.

Элементарной дизъюнкцией называется дизъюнкция любого числа булевых переменных, взятых с отрицанием или без него, в которой каждая переменная встречается не более одного раза. Элементарной дизъюнкцией, содержащей ноль переменных, будем считать константу 0.

Пример.

Элементарными дизъюнкциями для функции от одной переменной могут быть ,; для функции от двух переменных ,; для функции от трех переменных ,,и т.д.

Определение.

Конъюнктивной нормальной формой (КНФ) называется формула, представленная в виде конъюнкции элементарных дизъюнкций.

Пример.

Конъюнктивная нормальная форма функции может иметь вид.

Определение.

Члены конъюнктивной нормальной формы, представляющие собой элементарные конъюнкции букв, называютсямакстермами -го ранга.

Пример. Элементарная дизъюнкция является макстермом второго ранга; макстермом третьего ранга;  макстермом четвертого ранга.

Определение.

Конституентой нуля (макстермом -го ранга) называют булеву функцию аргументов, которая принимает значение, равное 0, только на одной интерпретации (наборе).

Пример.

Конституента нуля обращается в ноль только при одном соответствующем ей наборе значений переменных, который получается, если все переменные принять равными нулю, а их отрицания  единице, например, конституенте нуля соответствует набор (1010), конституенте нуля набор (001), конституенте нуля  набор (01).

Пример.

Представим в табл. 7.1 конституенты единицы и нуля, соответствующие интерпретациям функций трех переменных. Для каждой интерпретации функции имеются единственные соответствующие ей конституента единицы и конституента нуля.

Таблица 7.1  Конституенты единицы и нуля функций трех переменных

Номер интерпретации	Интерпретация			Конституента единицы	Конституента нуля
0	0	0	0
1	0	0	1
2	0	1	0
3	0	1	1
4	1	0	0
5	1	0	1
6	1	1	0
7	1	1	1

Различных конституент единицы и нуля для функции переменных имеется столько же, сколько и интерпретаций этой функции, т.е..

Определение.

Совершенной конъюнктивной нормальной формой (СКНФ) функции , содержащейразличных переменных, называется конъюнктивная нормальная форма, обладающая следующими свойствами:

а) в ней нет двух одинаковых множителей;

б) ни один множитель не содержит двух одинаковых слагаемых;

в) ни один множитель не содержит какой-нибудь переменной вместе с её отрицанием;

г) каждый множитель содержит в качестве слагаемого либо переменную , либо её отрицаниедля любого.

Условия а), б), в), г) являются необходимыми и достаточными для того, чтобы ДНФ была СДНФ.

Определение.

Совершенной конъюнктивной нормальной формой (СКНФ) булевой функции называется формула, представленная в виде конъюнкции конституент нуля данной функции.

В каждом члене СКНФ представлены все переменные (либо в прямом, либо в инверсном виде).

Всякая булева функция , которая не является тождественной единицей, имеет:

• несколько КНФ;

• одну и только одну СКНФ (количество её членов равно количеству единичных значений функции).

Различные нормальные формы (дизъюнктивные и конъюнктивные) можно получить, используя следующие основные подходы, в зависимости от того, каким способом представлена анализируемая булева функция:

• разложить булеву функцию по переменным;

• перейти от табличного представления функции к алгебраическому;

• преобразовать произвольную формулу алгебры логики в нормальную форму, проводя тождественные (эквивалентные) преобразования (используя законы (тождества) алгебры логики).

7.3 Теоремы о разложениях булевой функции по переменным

Рассмотрим теоремы о разложениях булевой функции по переменным. Для упрощения математических выкладок введем двоичный параметр и обозначениеследующим образом:;

и .

Бинарная функция представляется формулой.

Теорема о дизъюнктивном разложении булевой функции попеременным.

Любую булеву функцию можно представить в следующей форме .

Запись означает многократную дизъюнкцию, которая берется по всем возможным наборам значенийпри любом .

Следствие 1. Дизъюнктивное разложение булевой функции по одной переменной.

Любую булеву функцию можно представить в следующей форме .

Запись означает, что дизъюнкция берется по всем значениям, то есть по 0 и по 1. Записьобозначает значениефункции на наборе , где вместо значения переменнойподставлено.

Следствие 2. Дизъюнктивное разложение булевой функции по всемпеременным.

Любую булеву функцию можно представить в следующей форме:.

Запись означает, что дизъюнкция берется по всем наборам значений, на которых.

Пример.

Запишем дизъюнктивное разложение функции по всем переменным.

Определим значение функции на каждой интерпретации: ,,

, ,

, ,

, .

Запишем формулу, используя следствие 2 теоремы о разложении функций:

.

СДНФ функции является результатом дизъюнктивного разложения функции по всем переменным. СДНФ функции содержит только , следовательно, применив к СДКФ принцип двойственности, можно получить двойственное представление, которое называется конъюнктивным разложением.

Теорема о конъюнктивном разложении булевой функции попеременным.

Любую булеву функцию можно представить в следующей форме .

Запись означает многократную конъюнкцию, которая берется по всем возможным наборам значенийпри любом .

Следствие 3. Конъюнктивное разложение булевой функции по одной переменной.

Любую булеву функцию можно представить в следующей форме .

Запись означает, что конъюнкция берется по всем значениям, то есть по 0 и по 1. Записьобозначает значениефункции на наборе , где вместо значения переменнойподставлено.

Следствие 4. Конъюнктивное разложение булевой функции по всемпеременным.

Любую булеву функцию можно представить в следующей форме:.

Запись означает, что конъюнкция берется по всем наборам значений, на которых.

Пример.

Запишем конъюнктивное разложение функции по всем переменным. Определим значение функции на каждой интерпретации:

, ,

, ,

, ,

, .

Запишем формулу, используя следствие 4 теоремы о разложении функций

СКНФ функции является результатом конъюнктивного разложения функции по всем переменным.

7.4 Переход от табличного представления функции к алгебраическому представлению функции

Любая таблично заданная функция алгебры логики может быть представлена в виде или в виде,

где  элементарная конъюнкция ранга (конституента единицы);

 номера наборов, на которых функция равна 1, а функцияравна 0;

символ обобщенной дизъюнкции;

элементарная дизъюнкция ранга (конституента нуля);

символ обобщенной конъюнкции.

Для перехода от таблицы истинности булевой функции к СДНФ можно воспользоваться следующим алгоритмом:

а) выделить в таблице истинности все интерпретации, на которых значение функции равно единице;

б) записать конституенты единицы, соответствующие отмеченным интерпретациям;

в) получить СДНФ функции посредством соединения операцией дизъюнкции записанных конституент единицы.

Пример.

Получим СДНФ для функции .

Используем алгоритм перехода от таблицы истинности к алгебраическому представлению функции.

а) построим таблицу истинности функции и отметим интерпретации, на которых функция равна единице (табл. 7.2).

Таблица 7.2  Функция , заданная в табличном виде

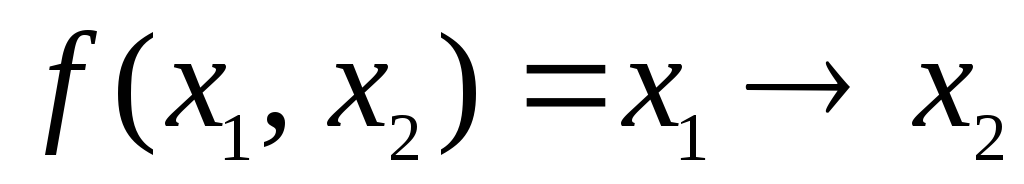
0	0	1
0	1	1
1	0	0
1	1	1

б) запишем конституенты единицы, соответствующие отмеченным интерпретациям: ,,.

в) получим СДНФ функции посредством соединения операцией дизъюнкции записанных конституент единицы

Для перехода от таблицы истинности булевой функции к СКНФ можно воспользоваться следующим алгоритмом:

а) выделить в таблице истинности все интерпретации, на которых значение функции равно нулю;

б) записать конституенты нуля, соответствующие отмеченным интерпретациям;

в) получить СКНФ функции посредством соединения операцией конъюнкции записанных конституент нуля.

Пример.

Получить СКНФ для функции .

Используем алгоритм перехода от таблицы истинности к алгебраическому представлению функции.

а) построим таблицу истинности функции и отметим интерпретации, на которых функция равна нулю (табл. 7.3).

Таблица 7.3  Функция , заданная в табличном виде

0	0	1
0	1	1
1	0	0
1	1	1

б) запишем конституенту нуля, соответствующую отмеченной интерпретации: .

в) получим СКНФ функции: .

Обратный переход от алгебраического к табличному представлению функции выполняется путем последовательной подстановки в данное алгебраическое выражение всех возможных наборов переменных, определения соответствующих значений для каждого-го набора и заполнения таблиц истинности.

7.5 Правила преобразования произвольной формулы алгебры логики в нормальную форму с использованием законов булевой алгебры

Для любой формулы алгебры логики путем равносильных (тождественных) преобразований можно получить её нормальную форму, причем не единственную.

Рассмотрим правила преобразования произвольной формулы алгебры логики к ДНФ (КНФ) и СДНФ (СКНФ), представленные в виде следующего алгоритма:

1. Исключить константы, используя законы действия с константами.

2. Опустить знаки отрицания непосредственно на переменные, используя законы де Моргана.

3. Используя дистрибутивный закон, раскрыть скобки (для получения КНФ  используя дистрибутивный закон привести функцию к виду конъюнкции элементарных дизъюнкций). К полученным элементарным конъюнкциям (дизъюнкциям) применить законы идемпотентности и противоречия (для получения КНФ  идемпотентности и исключенного третьего), упростить их и привести подобные. Результатом выполнения указанных действий является получение ДНФ (КНФ) булевой функции.

4. Построить конституенты единицы (нуля) введением в каждую элементарную конъюнкцию (дизъюнкцию) недостающих переменных, используя закон исключенного третьего (для получения СКНФ  закон противоречия).

5. С помощью дистрибутивного закона раскрыть скобки и привести подобные (для получения СКНФ  используя дистрибутивный закон привести функцию к виду конъюнкции конституент нуля и упростить формулу), используя закон идемпотентности. Полученная формула соответствует СДНФ (СКНФ) функции.

Пример.

Построим СДНФ функции .

Воспользуемся правилами преобразования произвольной формулы алгебры логики к СДНФ. Опускаем отрицания на переменные, используя закон де Моргана:

Построим ДНФ, используя дистрибутивный закон, законы идемпотентности и противоречия:

.

Так как функция зависит от трех переменных, то в элементарные конъюнкции необходимо ввести недостающие переменные, используя закон исключенного третьего: .

Используя дистрибутивный закон, раскроем скобки и приведем подобные для получения СДНФ:

.

Получена СДНФ заданной функции:

.

7.6 Контрольные вопросы и задания

1. На примере булевых функций опишите понятие «нормальной формы» функции.

2. Что представляет собой элементарная конъюнкция, элементарная дизъюнкция?

3. Какая формула называется дизъюнктивной нормальной формой, конъюнктивной нормальной формой?

4. Дайте определение понятиям минтерм, макстерм, конституанта единицы, конституанта нуля.

5. Что такое совершенная нормальная форма и какими свойствами она обладает?

6. Сколько имеется различных конституент единицы и нуля для функции переменных?

7. Сколько ДНФ и сколько СДНФ может иметь булева функция?

8. Запишите формулы дизъюнктивного разложения булевых функций от переменных попеременным, по всемпеременным, по одной переменной.

9. Запишите формулы конъюнктивного разложения булевых функций от переменных попеременным, по всемпеременным, по одной переменной.

10. Опишите алгоритмы перехода от таблицы истинности булевой функции к СДНФ и СКНФ.

11. Сформулируйте правила преобразования произвольной формулы алгебры логики в нормальную форму с использованием законов булевой алгебры.

Лекция 8. Минимизация булевых функций

8.1Основные понятия минимизации булевых функций. Критерии минимизации.

Функция алгебры логики может быть представлена различными формулами (в частности, различными ДНФ и КНФ), а, следовательно, практически может быть реализована различными эквивалентными функциональными схемами.

Пример.

Функция , заданная вектором, может быть представлена в виде СДНФи реализована при помощи соответствующих логических элементов. С другой стороны, эта функция может быть представлена другой ДНФс меньшим количеством букв и символов логических операций, а, следовательно, реализована другой логической схемой.

При решении практических задач из множества эквивалентных схем можно (и необходимо) выделить (синтезировать) наиболее экономичную или хотя бы достаточно простую схему, которая реализует рассматриваемую булеву функцию в некотором базисе. Данный базис обусловлен имеющимся в распоряжении проектировщика набором логических элементов или выбирается по соображениям наибольшей простоты реализации данного класса функций. Чаще всего задачу синтеза схем связывают с базисом, состоящим из отрицания, дизъюнкции и конъюнкции, который будем называть булевым базисом.

Пример.

Функция в булевом базисе преобразуется к виду:

.

Если в качестве базиса приняты отрицание и импликация, то функция будет иметь вид .

Для оценки формы булевой функции, которая наиболее предпочтительна для практической реализации, обычно вводится индекс (коэффициент) простоты , где  формула, реализующая функцию, характеризующий «сложность» ДНФ (КНФ). Наиболее часто встречаются следующие виды коэффициентов простоты:

а)  число символов (букв) переменных, встречающихся в записи ДНФ (КНФ);

б)  число элементарных конъюнкций (дизъюнкций), входящих в ;

в)  число символов инверсий, встречающихся в записи ДНФ (КНФ).

Пример.

Сравним две формулы и, реализующие одну функцию. Для них:и, следовательнопроще, чем;и, следовательно,проще, чем;и, следовательно,проще, чем.

8.2 Основные определения, используемые при минимизации булевых функций

Рассмотрим некоторые определения, используемые при минимизации булевых функций.

Определение.

Импликантой некоторой функции называется функция, такая, что на всех интерпретациях, на которыхравна единице,тоже равна единице.

Минтермы любого ранга, входящие в состав ДНФ функции, являются её импликантами.

Определение.

Множество , состоящее из импликант функции, называетсяпокрытием (или полной системой импликант) функции , если каждое единичное значение функциипокрывается единицей хотя бы одной импликанты из множества.

Пример.

Набор импликант, составляющих ДНФ функции, является её покрытием. Набор всех конституент единицы функции, входящих в её СДНФ, является покрытием данной функции.

Всякая элементарная конъюнкция , входящая в состав элементарной конъюнкциии содержащая меньше переменных, чем конъюнкция, называетсясобственной частью конъюнкции , и говорят, что конъюнкцияпокрывает конъюнкцию .

Определение.

Простой импликантой функции называется такая конъюнкция-импликанта, что никакая её собственная часть не является импликантой данной функции.

Множество всех простых импликант функции составляет покрытие данной функции.

Определение.

Дизъюнкция всех простых импликант функции называется её сокращенной ДНФ.

Определение.

Дизъюнктивным ядром булевой функции называется такое множество её простых импликант, которое образует покрытие, но после удаления импликанты теряет это свойство, то есть перестает быть полной системой импликант.

Определение.

Тупиковой ДНФ называется ДНФ данной булевой функции, состоящая только из простых импликант.

В отличие от сокращенной ДНФ, тупиковая ДНФ может не содержать некоторые из простых импликант функции. Каждая булева функция имеет единственную сокращенную ДНФ и может иметь несколько тупиковых ДНФ. В каждую из тупиковых ДНФ входят все импликанты дизъюнктивного ядра данной функции. |Тупиковые ДНФ могут иметь различную сложность и отличаться от минимальных. Среди тупиковых ДНФ всегда содержатся и минимальные ДНФ.

Определение.

Минимальной ДНФ (МДНФ) булевой функции называется одна из её тупиковых ДНФ, которой соответствует наименьшее значение критерия минимизации (индекса простоты) ДНФ.

Пример.

Пусть имеется функция , заданная в виде СДНФ:

.

Выполним операции полного склеивания следующим образом:

Операцию склеивания можно выполнить другим способом:

.

В обоих случаях получены тупиковые ДНФ функции . Вторая тупиковая ДКФ проще первой, поскольку содержит меньшее количество символов переменных и знаков операций.

Для анализа различных представлений булевой функции через КНФ и получения минимальных КНФ (МКНФ) необходимо использовать принцип двойственности. Двойственные понятия соответственно называются терминами: имплицента, простая имплицента, полная система имплицент, сокращенная КНФ, тупиковая КНФ, минимальная КНФ.

Проблема синтеза логических схем в булевом базисе связана с задачей минимизации булевых функций, которая в общем случае имеет две постановки:

• в аналитической форме;

• в геометрической форме (задача о покрытии).

Употребляются два языка: аналитический и геометрический.

Для решения данной задачи в современной теории и практике алгебры логики существуют следующие основные подходы:

• перебор (просмотр) всех возможных ДНФ и КНФ произвольной функции с целью поиска минимальной формы (первый подход);

• упрощение конкретной функции, достигаемое путем различных тождественных преобразований, с целью получения формулы, эквивалентной исходной, но реализуемой проще (второй подход).

Процесс перебора всех возможных ДНФ и КНФ функции является, хотя и наиболее понятным, но достаточно трудоемким процессом. Им нельзя воспользоваться практически уже с , а дляипроблема является тривиальной.

Процесс поиска минимальных форм становится более наглядным и целеустремленным, если использовать второй подход, т.е. некоторые аналитические и графические представления и специально разработанную для этой цели символику.

В общем случае минимальные формы булевых функций аналитически получают в такой последовательности:

• получают и анализируют конкретную функцию алгебры логики, определенную для всевозможных наборов значений аргументов;

• полученную функцию представляют через основные операции в любой из двух совершенных нормальных форм (СДНФ или СКНФ);

• находят сокращенную ДНФ (КНФ) (любая функция имеет одну такую форму);

• находят возможные тупиковые ДНФ (КНФ);

• из полученных тупиковых форм выбирают минимальные ДНФ (КНФ).

Для нахождения упрощенного аналитического выражения используются следующие очевидные преобразования формул булевой алгебры, которые традиционно называются «операциями».

Рассмотрим данные операции, принимая следующие обозначения:  некоторая элементарная конъюнкция переменных;  некоторая элементарная дизъюнкция переменных;  булева переменная.

Операция неполного дизъюнктивного склеивания:

.

Операция дизъюнктивного поглощения:

.

Выполнение двух указанных операций последовательно представляет собой выполнение операции полного дизъюнктивного склеивания:

.

Операция неполного конъюнктивного склеивания:

.

Операция конъюнктивного поглощения:

.

Операция полного конъюнктивного склеивания:

.

8.3 Основные методы минимизации булевых функций. Метод минимизирующих карт (диаграммы Карно-Вейча)

Существует несколько известных аналитических и геометрических методов получения минимальных ДНФ (КНФ): метод Квайна−Мак-Класки, метод Порецкого-Блейка, метод минимизирующих карт (диаграммы Карно-Вейча), метод многомерных кубов и др.

Целью минимизации является нахождение минимальной из тупиковых ДНФ (КНФ), т.е. нахождение минимального покрытия данной функции. Для этого необходимо построить все возможные тупиковые ДНФ (КНФ), используя операции склеивания и поглощения для данной функции. Методика использования минимизирующих карт (методика диаграмм Карно и Вейча) позволяет выполнить указанные операции графически. Диаграммы Карно-Вейча представляют собой развертки кубов на плоскости.

Карты Карно (диаграммы Вейча) представляют собой специально организованные таблицы соответствия (истинности). Значения не более двух переменных располагаются в заголовках строк и столбцов карты в таком порядке, что каждый последующий отличается от предыдущего значением только одной из переменных, например, (0, 0), (0, 1), (1, 1), (1, 0). Клетки, расположенные по краям таблицы, считаются соседними и обладают этим свойством.

Каждой конституенте соответствует одна ячейка таблицы. Нуль или единица в ячейке определяет значение функции на данной интерпретации.

При таком расположении минтермы (макстермы), к которым применима операция склеивания, располагаются в соседних ячейках карты, и склеивание производится графически посредством объединения ячеек в группы.

Пример.

Карты Карно для функций двух переменных имеют вид таблицы (табл. 8.1), где столбцы соответствуют значениям первой переменной, а строки − значениям второй переменной функции(в ячейках указаны соответствующие минтермы в виде формул с абстрактными переменными).

Таблица 8.1 − Структура карты Карно для двух переменных

	0	1
0
1

Пример.

Структура карты Карно для функции трех переменных имеет вид таблицы(в ячейках указаны соответствующие минтермы в виде формул с абстрактными переменными) (см. табл. 8.2).

Таблица 8.2 − Структура карты Карно для трех переменных

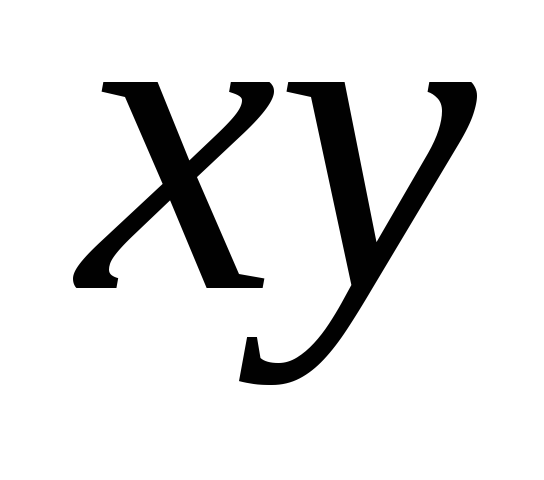
	00	01	11	10
0
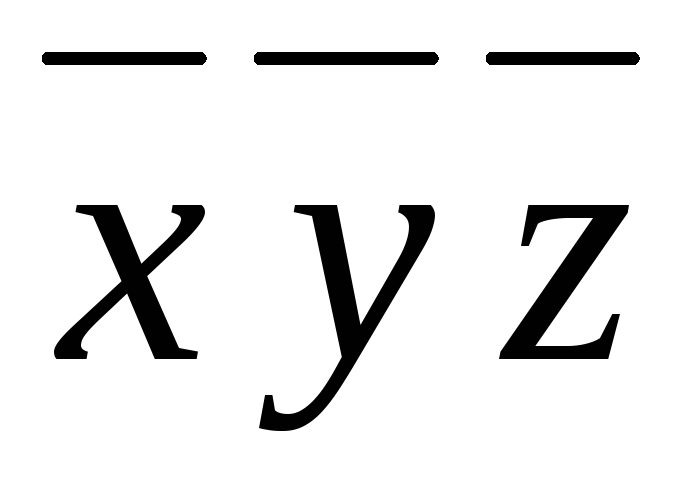
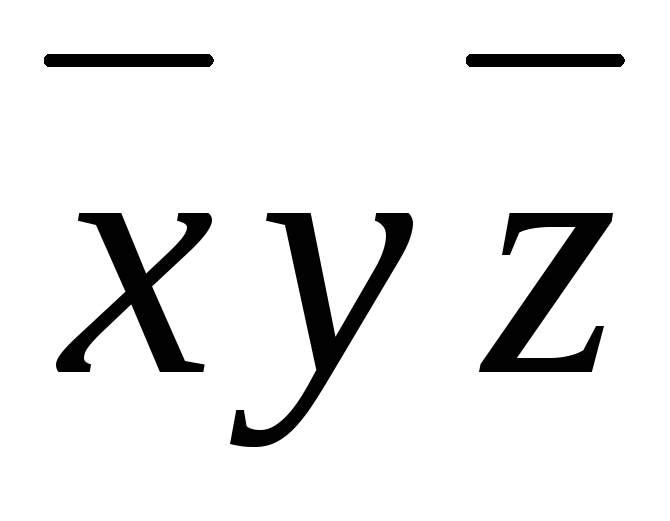
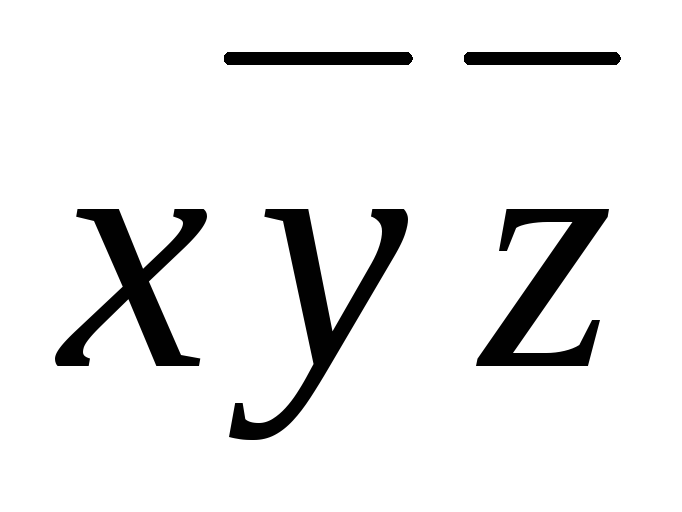
1

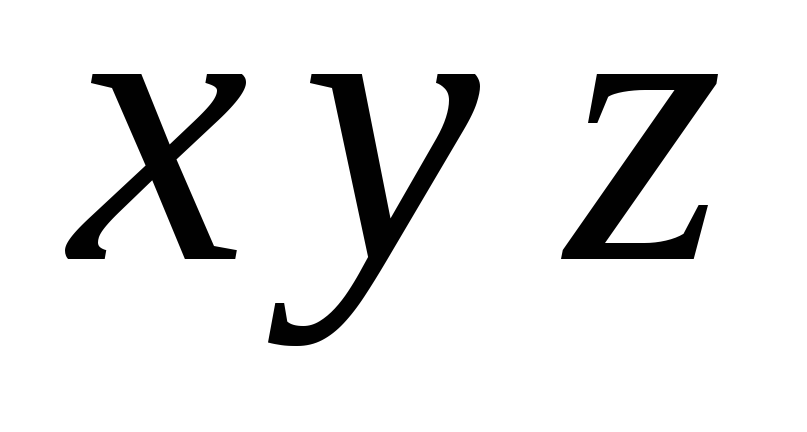
Для конкретной булевой функции карта Карно заполняется следующим образом. В ячейки, соответствующие интерпретациям, на которых функция равна единице, записывают единицы. Указанные ячейки соответствуют конституентам единицы, присутствующим в СДНФ функции. В остальные ячейки записывают нули.

Пример.

Построить карту Карно для функции .

В ячейки таблицы, соответствующие минтермам данной СДНФ, записываем единицы, в остальные ячейки − нули (см. табл. 8.3).

Таблица 8.3 − Карта Карно для функции

	00	01	11	10
0	1	0	0	0
1	1	1	1	0

К конституентам единицы, соответствующим любым двум соседним ячейкам, можно применить операцию склеивания, так как они отличаются только одной переменной. На карте Карно для функции трех переменных каждая ячейка имеет три соседние ячейки, на карте Карно для функции четырех переменных − четыре, на карте Карно для функции пяти переменных − пять и т.д.

При минимизации на множестве ДНФ в склеивании участвуют только ячейки, содержащие единицы. Как правило, в картах Карно нули в ячейках не указывают, оставляя данные ячейки пустыми.

Пример.

В таблицах 8.4 и 8.5 приведены карты Карно для трех переменных с отмеченными соседними ячейками для ячеек А и В.

Таблица 8.4 − Карта Карно для функции с отмеченными соседними ячейками для ячейки А

	00	01	11	10
0			А
1

Таблица 8.5 − Карта Карно для функции с отмеченными соседними ячейками для ячейки В

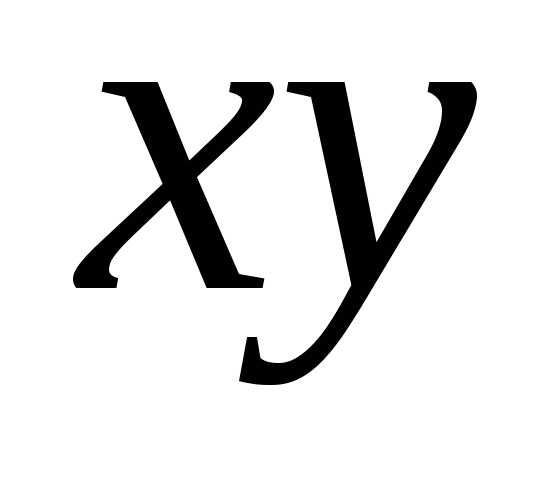
	00	01	11	10
0				В
1

Правило склеивания ячеек и записи минимальной ДНФ:

1. Строится карта Карно, соответствующая данной функции.

2. Ячейки объединяются в группы, обозначающие операции склеивания. В объединении участвуют только соседние ячейки, в которых находятся единицы. В группу объединяется только то количество ячеек, которое равно . При этом группа может иметь только прямоугольную или квадратную форму.

3. Решается задача склеивания, которая заключается в нахождении набора максимальных групп ячеек. Максимальная группа − это группа, которая не входит целиком ни в одну другую группу и соответствует простой импликанте функции. Количество групп в таком наборе должно быть минимальным, так как такая группа соответствует минимальной тупиковой ДНФ. Каждая единица карты Карно должна входить хотя бы в одну группу, что обеспечивает покрытие функции полученным набором импликант.

4. Каждая группа ячеек, полученная после склеивания, соответствует той импликанте функции, реальные переменные которой имеют одинаковое значение для всех ячеек группы. Переменные берутся без отрицания, если им соответствуют единичные значения, и с отрицанием − в противном случае.

5. Дизъюнкция всех полученных простых импликант представляет собой результат минимизации формулы и является минимальной ДНФ.

Пример.

Найти минимальную ДНФ функции .

Запишем исходную карту Карно для заданной функции (табл. 8.6).

Таблица 8.6 − Исходная карта Карно для заданной функции

	00	01	11	10
0	1	0	0	0
1	1	1	1	0

Используем графический способ склеивания, объединяя соседние единицы таблицы в группы (нули опускаем). Результатом являются две импликанты А и В (рис. 8.1).

Рисунок 8.1 − Определение импликант функции

Импликанта .

Импликанта .

Таким образом, получим минимальную ДНФ в виде .

Карта Карно для функции четырех переменных имеет размер . Правила склеивания ячеек и записи результирующей формулы остаются прежними.

Рассмотрим построение карты Карно для функции пяти переменных, которая представляет в пространстве двухслойный параллелепипед, где каждый слой соответствует карте Карно от первых четырех переменных функции. Первый слой представляет собой на плоскости всевозможные интерпретации, при которых пятая переменная равна нулю. Вторым слоем являются всевозможные интерпретации, при которых пятая переменная равна единице. Каждая ячейка на карте Карно для функции пяти переменных имеет пять соседних ячеек: четыре на своем слое карты и пятую − на соседней, т.е. ячейку, которая совпадает с данной, если разместить слои карты один поверх другого. Объединение ячеек в группы на каждом слое карты осуществляется, как и в случае четырех переменных. В данном случае можно склеивать две одинаковые группы, находящиеся на разных слоях карты, расположение которых совпадает, если поместить один слой карты поверх другого.

Пример. Построить минимальную ДНФ для функции

.

Построим карту Карно для данной функции (рис. 8.2).

Рисунок 8.2 − Карта Карно для функции

Простые импликанты, входящие в минимальную ДНФ, имеют вид: ,,,,.

Минимальная ДНФ записывается при объединении импликант знаками дизъюнкции:.

Минимизация на множестве КНФ. Для минимизации булевой функции на множестве КНФ используются диаграммы Вейча, построение которых аналогично построению карт Карно. Отличие заключается в том, что на карте помечаются ячейки, соответствующие интерпретациям, на которых функция равна нулю. После этого производится склеивание ячеек, содержащих нули и формирование минимальной КНФ. Для склеивания ячеек используются те же правила, что и при получении минимальной ДНФ. Каждая группа ячеек, полученная в результате склеивания, соответствует дизъюнкции только тех переменных, которые имеют одинаковое значение для всех ячеек группы. Переменные берутся без отрицания, если им соответствует нулевое значение, и с отрицанием − в противном случае. Конъюнкция полученных элементарных дизъюнкций является результатом минимизации формулы.

Пример.

Построить минимальную КНФ функции, заданной картой Карно (диаграммой Вейча), представленной в табл. 8.7.

Таблица 8.7 − Карта Карно (диаграмма Вейча) для функции

	00	01	11	10
00	1	1	0	1
01	0	0	0	0
11	0	0	0	1
10	1	1	0	1

Для получения МКНФ необходимо рассмотреть «нулевые» ячейки, максимизируя размеры их групп и минимизируя количество таких групп, и провести операцию склеивания (рис. 8.3).

Рисунок 8.3 − Карта Карно (диаграмма Вейча) для булевой функции

Запишем минимальную КНФ, объединив знаками конъюнкции элементарные дизъюнкции: .

Минимизация частично определенных функций с использованием карт Карно. Для решения некоторых задач могут использоваться не все наборы входных данных, поэтому допустимо любое значение функции на неиспользуемых интерпретациях. Такая функция называется частично определенной. При минимизации такие функции доопределяются так, чтобы получить наиболее экономичную минимальную ДНФ (КНФ).

8.4 Контрольные вопросы и задания

1. Что представляет собой булевый базис? Чем обусловлен выбор базиса при проектировании логических схем?

2. Что представляет собой индекс (коэффициент) простоты? Приведите примеры индексов простоты.

3. Какие существуют подходы для решения задачи минимизации булевых функций в аналитическом виде?

4. Запишите формулы операций дизъюнктивного склеивания и поглощения.

5. Запишите формулы операций конъюнктивного склеивания и поглощения.

6. Дайте определение терминам «импликанта», «имплицента», «простая импликанта», простая «имплицента».

7. Что представляет собой сокращенная ДНФ и сокращенная КНФ?

8. Дайте определение тупиковой ДНФ. Сколько тупиковых ДНФ может иметь булева функция?

9. Какая из ДНФ (КНФ) называется минимальной ДНФ (минимальной КНФ)?

10. Что представляют собой карты Карно (диаграммы Вейча)?

11. Назовите правило склеивания ячеек и записи минимальной ДНФ при использовании карт (диаграмм) Карно.

12. Как осуществляется построение карты Карно для функции пяти переменных?

13. Опишите особенности минимизации булевых функций на множестве КНФ с использованием минимизирующих карт.

14. Каким образом осуществляется минимизация частично определенных функций?

Лекция 9. Алгебра Жегалкина и линейные функции.Функциональная полнота наборов булевых функций

9.1 Алгебра Жегалкина и линейные функции

9.1.1 Основные определения алгебры Жегалкина

Алгебра Жегалкина, названная по имени предложившего её советского ученого, строится на основе операций сложения по модулю 2 и конъюнкции.

Определение.

Алгебра , образованная множествомвместе с операциями конъюнкции (), суммы по модулю 2 () и константами 0 и 1, называетсяалгеброй Жегалкина.

Пример.

Пусть  булевы переменные, тогда формула , содержащая только операции конъюнкции и суммы по модулю 2, является формулой алгебры Жегалкина.

Непосредственной проверкой по таблицам истинности можно установить следующие основные тождества (свойства этой алгебры):

1) , коммутативность;

2) , ассоциативность;

3)  дистрибутивность относительно;

4)  свойства констант.

Все эти свойства подобны обычной алгебре, но в отличие от булевой алгебры закон дистрибутивности суммы по модулю 2 относительно конъюнкции не имеет силы .

Справедливы также следующие тождества:

5)  закон идемпотентности для ;

6)  закон приведения подобных при выполнении операции суммы по модулю 2.

Таким образом, в алгебре Жегалкина, как и в булевой алгебре, не могут появляться коэффициенты при переменных и показатели степени.

В алгебре Жегалкина используются следующие соотношения, позволяющие перейти от любой формулы булевой алгебры к соответствующей ей формуле алгебры Жегалкина ,и наоборот.

Доказательство данных тождеств можно осуществить, используя таблицы истинности функций, либо аналитически, путем тождественных преобразований формул.

Пример. Докажем тождество , используя таблицы истинности функции (табл. 9.1).

Таблица 9.1  Таблица истинности функций и

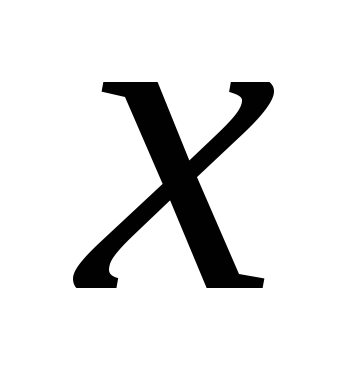
0	1	1
1	0	0

Пример.

Докажем формулу аналитически следующим образом:

.

Через операции алгебры Жегалкина можно выразить все другие булевы функции:

;

;

;

;

.

9.1.2 Полином Жегалкина

Среди всех эквивалентных представлений функции в алгебре Жегалкина выделяется особый вид формул, называемый полиномом Жегалкина.

Определение.

Полиномом Жегалкина называется конечная сумма по модулю 2 попарно различных элементарных конъюнкций над множеством переменных . Количество переменных, входящих в элементарную конъюнкцию, называетсярангом элементарной конъюнкции. Количество попарно различных элементарных конъюнкций в полиноме называется длиной полинома.

Представление в виде полинома существует и единственно для каждой булевой функции.

Теорема.

Всякая булева функция может быть представлена каноническим полиномом Жегалкина, причем это представление единственное с точностью до перестановки слагаемых и их сомножителей. Для любой булевой функции существует единственный полином Жегалкина.

Для определения полинома Жегалкина можно использовать следующие основные методы:

• метод тождественных преобразований;

• метод неопределенных коэффициентов.

При использовании метода тождественных преобразований для построения полинома Жегалкина функции, заданной некоторой формулой алгебры Жегалкина, необходимо: раскрыть все скобки в данной формуле по закону дистрибутивности и произвести все возможные упрощения с использованием законов действия с константами, идемпотентности и приведения подобных.

Пример.

Представить полиномом Жегалкина логическую функцию импликацию ().

Вначале запишем СДНФ данной функции, затем выразим операции дизъюнкции и отрицания через конъюнкцию и сумму по модулю 2. получив формулу алгебры Жегалкина, пользуясь методом тождественных преобразований, получим полином Жегалкина:

.

9.1.3 Метод неопределенных коэффициентов для нахождения полинома Жегалкина

Метод неопределенных коэффициентов, который можно использовать для нахождения полинома Жегалкина заданной функции, рассмотрим на примере.

Пример. Построить полином Жегалкина для функции импликации с использованием метода неопределенных коэффициентов.

Запишем полином для данной функции в виде суммы по модулю 2 всех возможных элементарных конъюнкций для с неопределенными коэффициентами, где коэффициентыпринимают значения из множестваи определяют присутствие или отсутствие элементарной конъюнкции в полиноме. Найдем последовательно значения коэффициентов, подставляя значения переменных и функции на различных интерпретациях:,, следовательно. Далее проводим вычисления,, следовательно,. Проводим преобразования на следующей интерпретации,, откуда следует. На последней интерпретации:,.

Подставив полученные значения коэффициентов , получим полином Жегалкина для функции

.

Полином Жегалкина, который может быть построен для каждой булевой функции, позволяет определить одно из её важных свойств  линейность.

Определение.

Булева функция называется линейной, если она представляется в алгебре Жегалкина каноническим многочленом (полиномом Жегалкина), не содержащем конъюнкций переменных:, где коэффициенты, принимающие значение 0 или 1.

Так как всего коэффициентов , то число различных линейных многочленов будет. В силу однозначности представления функции полиномом Жегалкина это число выражает и количество линейных функций.

Обозначим через класс линейных функций.

Пример.

Отрицание является линейной функцией, т.к. её полином Жегалкина () не содержит конъюнкций переменных. Дизъюнкция является нелинейной функцией, поскольку её полином Жегалкина () содержит конъюнкцию переменныхи. Импликация является нелинейной функцией, так как её полином Жегалкина () содержит конъюнкцию переменныхи. Эквивалентность является линейной функцией, поскольку её полином Жегалкина ()не содержит конъюнкций переменных.

9.2 Функциональная полнота булевых функций

9.2.1 Типы булевых функций

В алгебре логики из множества различных булевых функцийпеременныхвыделяются следующие пять типов булевых функций:

а) функции, сохраняющие константу 0;

б) функции, сохраняющие константу 1;

в) самодвойственные функции;

г) монотонные функции;

д) линейные функции.

Определение.

Булева функция называетсяфункцией, сохраняющей 0, если на нулевой наборе она равна 0, т.е. .

Так как на одном из наборовзначения таких функций фиксированы, то их число равно, то есть половина всех функцийпеременных сохраняет константу 0.

Обозначим через класс функций, сохраняющих 0.

Определение.

Булева функция называетсяфункцией, сохраняющей 1, если на единичном наборе она равна 1, т.е. .

Их число, как и в предыдущем случае, равно половине общего числа всех функций переменных. Обозначим черезкласс функций, сохраняющих 1.

Пример.

Функции исохраняют 0 и сохраняют 1, так как,и,. Функцияне сохраняет 0 и не сохраняет 1, так каки.

Самодвойственная функция (см. раздел «Принцип двойственности») полностью определяется заданием её значений на половине всех наборов (остальные значения определяются по условию антисимметричности), поэтому число независимых наборов равно и число всех таких функций. Обозначим черезкласс самодвойственных функций.

Рассмотрим важный класс булевых функций  монотонные булевы функции. Обозначим через класс монотонных функций.

Зададим два любых набора булевых констант (две интерпретации) в виде и, на которых введем отношение частичного порядка(отношение предшествования).

Определение.

Для двух наборов ивыполняется отношение предшествования, если.

Если хотя бы для одной пары , где, отношениене выполняется, то соответствующие им наборыив отношении порядка не участвуют, т.е. являются несравнимыми.

Пример. Два набора инаходятся в отношении предшествования, т.к., ().

Наборы же (0, 1) и (1, 0) не находятся в отношении предшествования.

Определение.

Функция называетсямонотонной, если для любых двух наборов и, находящихся в отношении предшествования, имеет место и неравенство.

Функция, эквивалентная монотонной, является также монотонной. Для проверки функции на монотонность необходимо исследовать выполнение неравенства для всех пар наборов.

Пример. Константы 0 и 1 и функция монотонны. Отрицаниенемонотонно. Дизъюнкция и конъюнкция любого числа переменных являются монотонными функциями.

Пример.

Проведем анализ на монотонность двух функций от трех переменных, заданных таблицей истинности (табл. 9.2).

Таблица 9.2  Таблица истинности функций трех переменных и

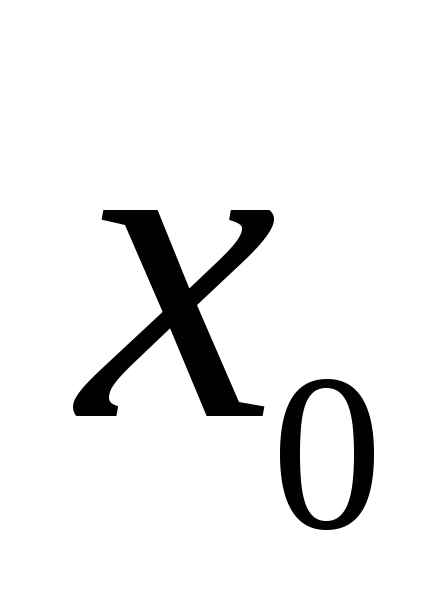
0	0	0	0	0
0	0	1	1	0
0	1	0	0	1
0	1	1	1	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

Функция немонотонная, так как, а. Функциямонотонна, т.к.для всех пар наборов.

Проверка монотонности функции непосредственно по определению требует анализа таблицы функции и может оказаться достаточно громоздкой. Поэтому воспользуемся следующей теоремой.

Теорема.

Всякая булева формула, не содержащая отрицаний, представляет монотонную функцию, отличную от 0 и 1, и наоборот, для любой монотонной функции, отличной от 0 и 1, найдется представляющая её булева формула без отрицаний.

Следствие.

Сокращенная ДНФ монотонной функции является её минимальной ДНФ.

Пример.

Определить, является ли функция монотонной.

Выразим через элементарные функции булевой алгебры:

.

Полученная формула булевой алгебры не содержит отрицаний, следовательно, функция является монотонной.

9.2.2 Замкнутые классы булевых функций

Рассмотрим понятия замыкания и замкнутого класса.

Определение.

Пусть  некоторое подмножество функций из .Замыканием множества булевых функций называется множество , состоящее из функций, представимых в виде формул через функции множества.

Пример.

а) , очевидно;

б) , замыканием этого множества будет классвсех линейных функций, то есть функций, имеющих вид:, где.

Определение.

Класс (множество) называется замкнутым классом, если .

Пример.

а) класс − замкнутый класс;

б) класс не замкнут;

Всякий класс будет замкнутым.

Определение.

Важнейшими замкнутыми классами булевых функций, которые называются классами Поста, являются:

−класс функций, сохраняющих 0;

−класс функций, сохраняющих 1;

−класс самодвойственных функций;

−класс монотонных функций;

−класс линейных функций.

Булева функция может принадлежать одному или нескольким классам Поста, а может не входить ни в один класс.

Пример.

Функция входит в класс линейных функцийи в класс функций, сохраняющий 1. Функцияпринадлежит всем классам. Функция штрих Шефферане входит ни в один из классов.

Теорема 9.1 Каждый из классов Поста замкнут.

Замкнутые классы Поста попарно различны.

В табл. 9.3 приведем результаты исследования на принадлежность классам Поста каждой булевой функции двух переменных.

Таблица 9.3 − Принадлежность булевых функций классам Поста

Булева функция	Формула	Классы Поста
Константа 0	0	*	-	-	*	*
Конъюнкция		*	*	-	*	-
Отрицание импликации		*	-	-	-	-
Повторение первого аргумента		*	*	*	*	*
Отрицание обратной импликации		*	-	-	-	-
Повторение второго аргумента		*	*	*	*	*
Сумма по модулю 2	)	*	-	-	-	*
Дизъюнкция		*	*	-	*	-
Стрелка Пирса		-	-	-	-	-
Эквиваленция		-	*	-	-	*
Отрицание второго аргумента		-	-	*	-	*
Обратная импликация		-	*	-	-	-
Отрицание первого аргумента		-	-	*	-	*
Импликация		-	*	-	-	-
Штрих Шеффера		-		-	-	-
Константа 1	1	-	*		*	*

9.2.3 Понятия функциональной полноты булевых функций

Понятие полноты булевых функций имеет существенное практическое значение прежде всего в синтезе логических схем, где системе логических функций соответствует набор (серия) типовых логических элементов, а полнота системы означает возможность реализовать с помощью элементов данной схемы любые логические функции.

Определение.

Система функций из, которое является множеством всех возможных булевых функций, зависящих от любого числа переменных, называетсяфункционально полной, если любая булева функция может быть записана в виде формулы через функции этой системы (в виде суперпозиции функций из этой системы).

Пример.

Рассмотрим примеры полных и неполных систем:

а) система  множество булевых функций, является полной системой;

б) система представляет полную систему;

в) система не является полной.

Теорема 9.1

Пусть даны две системы функций ииз, относительно которых известно, чтоявляется полной и каждая её функция выражается в виде формулы через функции системы. Тогда систематакже является полной.

Опираясь на эту теорему, можно установить полноту ряда систем следующим образом:

а) представить (задать) функции в виде формул;

б) все операции в заменить формулами над.

Пример.

а) системы функций иявляются полными. Доказать, что систематакже является полной.

Действительно, из законов де Моргана и двойного отрицания следует, что в каждой из этих двух систем недостающая до функция выражается через остальные две:,. Следовательно, булева формулав системеперейдет в формулу, а в системе в формулу .

Определение.

Система функций из, суперпозицией которых может быть представлена любая функция из некоторого множества булевых функций и в которой допускаются константы 0 и 1, называетсяослаблено функционально полной или функционально полной в слабом смысле.

В терминах замкнутого класса можно дать следующее определение полноты.

Определение.

Система булевых функций называетсяфункционально полной, если .

Исходя из рассмотренных определений можно предположить, что не каждая система является полной. Пост предложил и исследовал условия, называемые критерием полноты, выполнение которых позволяет определить, является ли произвольная система булевых функций полной в сильном смысле.

Рассмотрим теорему полноты Поста, которая является основной теоремой о функциональной полноте булевых функций.

9.2.4 Теорема Поста о функциональной полноте

Для того чтобы система функций была функционально полной, необходимо и достаточно, чтобы она содержала хотя бы одну функцию, не сохраняющую ноль, хотя бы одну функцию, не сохраняющую единицу, хотя бы одну несамодвойственную функцию, хотя бы одну немонотонную функцию, хотя бы одну нелинейную функцию.

Одна и та же функция может представлять в функционально полной системе одно или несколько требуемых свойств, а также может обладать всеми пятью требуемыми свойствами. Следовательно, минимальное число булевых функций в функционально полном наборе равно единице.

Если каждая из взятых функций обладает лишь одним свойством (но каждая другим), то для функциональной полноты необходима система из 5-ти функций.

Говорят, что функционально полная система функций образует базис в логическом пространстве.

Определение.

Система функций называется минимально полным базисом, если удаление из неё любой функции превращает эту систему в неполную.

Определение.

Полная система булевых функций называется несократимой, если из неё нельзя исключить ни одной булевой функции без потери свойств полноты.

В связи с тем, что каждая из функций может обладать несколькими свойствами, функционально полные системы могут быть построены с помощью одной, двух, трех и четырех функций.

Пример.

Наиболее распространенная система − система из трех функций: отрицание, конъюнкция и дизъюнкция. С помощью этих функций могут быть описаны процессы управления любыми производственными процессами; функция, описывающая работу любого устройства вычислительной системы и т.п.

Пример.

Определить с помощью теоремы Поста, является ли система функционально полной?

Операцию отрицания можно представить полиномом Жегалкина в виде , следовательно, функция отрицания линейна. Функция отрицания является самодвойственной, не сохраняет), не сохраняет 1(определяется с использованием таблицы истинности), немонотонна. Импликация является нелинейной функцией, т.к. её полином Жегалкина имеет вид, она несамодвойственная, не сохраняет 0 , сохраняет 1 (можно определить по таблице истинности), немонотонна. Следовательно, для каждого класса Поста в данной системе имеется хотя бы одна функция, которая этому классу Поста не принадлежит. По теоремеПоста такая система булевых функций является функционально полной.

Теорема 9.2

Для того чтобы система функций была функционально полной в слабом смысле, необходимо и достаточно, чтобы она содержала хотя бы одну немонотонную и хотя бы одну нелинейную функцию.

Пример.

Система функционально полна в слабом смысле, так как конъюкнция нелинейно, а сумма по модулю 2 немонотонна. Константа 0 получается из соотношения, однако константу 1 с помощью конъюнкции и суммы по модулю 2 получить нельзя, поэтомуне является полной в обычном (полном) смысле. Использование константы 1, которое разрешается определением слабой полноты, сводитк полной в сильном смысле системе.

9.3 Контрольные вопросы и задания

1. Перечислите основные типы булевых функций.

2. Дайте определение булевых функций, сохраняющих 0 и 1.

3. Какое количество всех функций переменных сохраняет константу 0 и константу 1?

4. Какая функция называется монотонной?

5. Как по виду ДНФ булевой функции можно определить, монотонна функция или нет?

6. Поясните структуру алгебры Жегалкина.

7. Перечислите основные законы и тождества алгебры Жегалкина.

8. Определите понятие полинома Жегалкина.

9. Дайте определение линейности булевой функции.

10. Приведите примеры линейных и нелинейных функций двух переменных.

11. Перечислите важнейшие замкнутые классы булевых функций.

12. Какая система булевых функций называется функционально полной?

13. Сформулируйте теорему о полноте двух систем булевых функций.

14. Дайте определение функциональной полноты в слабом смысле.

15. Какая полная система булевых функций является несократимой.

16. Сформулируйте теорему Поста о полноте булевых функций.

Лекция 10. Логика высказываний. Алгебра высказываний.

10.1 Высказывания (основные понятия)

С древнейших времен человечеству известна логика, или искусство правильно рассуждать, причем способность к рассуждениям − это именно искусство. Имея какие-то утверждения (посылки), истинность которых проверена, скажем, на опыте, логик путем умозрительных построений приходит к другому утверждению (заключению), которое также оказывается истинным (в некоторых случаях). Опыт древних (число наблюдательный) был систематизирован Аристотелем, рассмотревшим конкретные виды рассуждений, которые назвал силлогизмами. Однако логика Аристотеля − это классическая логика, то есть наука, традиционно относящаяся к гуманитарному циклу.

Предметом этого раздела дисциплины «Дискретная математика» являются некоторые элементы логики математической.

С помощью алгебры логики (математической) можно описывать рассуждения и «вычислять» их результаты, если символам переменных поставить в соответствие некоторые утверждения, называемые высказываниями.

Такое применение алгебры логики получило название логики высказываний. Впоследствии оно было расширено добавлением переменных, принимающих значения из множества понятий, что сформировало логику предикатов.

Дальнейшее развитие логики высказываний основано на допущении нескольких значений истинности (например, кроме значений «истина» и «ложь» допускается третье значение − «неопределенность»). В подобных случаях используют аппарат многозначной логики. Если истинность предложений определяется с некоторой вероятностью, то логика высказываний превращается в вероятностную логику.

Понятие закона исключения третьего позволяет полностью использовать в логике высказываний аппарат двузначной логики (рассмотренный в разделе 3). В данном разделе дисциплины рассматривается только двузначная логика высказываний и логика предикатов.

План раздела состоит в том, чтобы на основе предварительного рассмотрения основных понятий логики высказываний и логики предикатов ввести понятие «формальной теории» и наиболее часто используемых исчислений: исчисления высказываний и исчисления предикатов.

Понимание основ теории доказательств, которая рассматривается в данном разделе, необходима для логического построения передовых компьютерных технологий.

Введем специфическую «логическую» терминологию и укажем её связь с положениями раздела «Элементы математической логики. Алгебра булевых функций».

Определение.

Высказывание – это утверждение или повествовательное предложение, о котором можно сказать, истинно оно или ложно, но ни то и другое одновременно.

В логике высказываний рассматривают не содержание и даже не структуру высказывания, а ограничиваются только тем его свойством, что оно представляет собой истину или ложь.

Пример.

Предложения, являющиеся высказываниями:

а) Два умножить на два равно четыре ().

б) Рим − столица Франции.

Предложения, не являющиеся высказываниями:

а) Кто Вы? (вопрос).

б) Прочтите эту книгу до следующего занятия (приказ или восклицание).

в) Это утверждение ложно (внутренне противоречивое утверждение).

Определение.

Высказывания, которые соответствуют простым повествовательным предложениям, т.е. не имеют составных частей, называются атомами (элементарными высказываниями, атомарными формулами).

Высказывание можно рассматривать как величину, (пропозициональную переменную, высказывательную переменную), которая может принимать два значения: «истина» и «ложь», т.е. принимать истинностное значение.

Определение.

Под истинностным значением понимается абстрактный объект («истина» или «ложь»), сопоставляемый высказыванию в зависимости от того, является это высказывание истинным или ложным. Обозначается: «истина» − И, Т (True) или 1, „ложь” – Л, F (False) или 0.

Определение.

Множество {И, Л} называется множеством истинностных значений.

Пример.

Высказывание «» имеет истинностное значение 1 (И).

Высказывание «Рим − столица Франции» имеет истинностное значение 0 (Л).

Можно рассматривать две группы высказываний:

• высказывания, истинностное значение которых независимо от ситуации можно считать однозначно определенным;

• высказывания, зависящие от обстоятельств, которыми руководствуются при его истолковании, и, следовательно, могут принимать различные значения.

Обычно эти обстоятельства не фигурируют явно в простом высказывании.

Пример.

а) Высказывание «» определено однозначно.

б) Истинность таких высказываний, как «Хорошая погода», «Сегодня 31 декабря», «Результат измерений диаметра цилиндра равен 52 мм» зависит, соответственно, от вкусов или критерия оценки погоды, сегодняшней даты, требуемой точности измерения. Высказывание «Завтра будет дождь» может получить значение «истина» или «ложь» в зависимости от конкретной ситуации.

качестве символов для обозначения атомов используются заглавные буквы латинского алфавита или заглавные буквы с индексами. Каждая буква в рассуждении должна обозначать одно и только одно элементарное высказывание.

Пример.

а)  «Снег белый».

б)  «Аня является студенткой университета».

в) − «Группа КН-13-1 насчитывает 25 студентов».

10.2 Логические связки и формулы логики высказываний

Рассматривая конструкции естественного языка, видим, что простые предложения объединяются в сложные при помощи соответствующих сентенциональных связок (союзов), т.е. сложные предложения состоят из простых предложений и служебных слов («если», «то», «и», «или» и т.п.).

Пример.

Составные (сложные) высказывания:

а) «Снег белый, и температура ниже нуля».

б) «Если Петр на занятиях, то Аня дома».

в) «Петр − студент института или шахтер».

Простые предложения и союзы можно использовать как элементы словаря, необходимого для формализации естественного языка с помощью логики высказываний. Операции логики высказываний – логические связки – рассматриваются как формальные обозначения соответствующих им связок естественного языка. Сентенциональные связки в разговорном языке допускают различные варианты. Поэтому при записи сложного предложения в виде формулы алгебры высказываний важно выяснить характер логической связи между предложениями, не вдаваясь в смысл этих предложений.

Из одних высказываний различными способами можно строить новые, более сложные высказывания, называемые формулами или молекулами, используя те же операции (и их символы), что и в булевой алгебре. Примеры связок и их символов приведены в табл. 10.1.

Таблица 10.1 − Логические связки в логике высказываний

Название	Обозначение	Аналоги естественного языка
Отрицание		не, «неверно, что»
Конъюнкция		и
Дизъюнкция		или, «или одно из двух …, или оба», либо
Импликация		влечет, «если, …то», «только если», «только тогда, когда», «есть достаточное условие», «при условии, что», «есть необходимое условие»
Эквивалентность		эквивалентно, равносильно, «тогда и только тогда, когда», «если и только если», «есть необходимое и достаточное условие»

Рассмотрим примеры и выражения естественного языка, которые соответствуют логическим связкам.

Определение.

Отрицанием высказывания называется высказывание (обозначение), которое истинно тогда и только тогда, когдаложно.

Данная унарная операция соответствует отрицанию в естественном языке, которое может иметь различные синтаксические выражения (см. таблицу 4.1).

Пример.

Пусть имеем высказывание − «Владимир получил электронное письмо от Александра». Отрицанием высказыванияявляется:− «Владимир не получил электронное письмо от Александра». Данное высказывание можно представить следующим образом:− «Неверно, что Владимир получил электронное письмо от Александра».

Определение.

Высказывание , называемоеконъюнкцией и, истинно тогда и только тогда, когда истинны оба высказыванияи.

Эта логическая операция соответствует в естественном языке связке «и», соединяющей два предложения.

Пример.

Пусть имеем простые высказывания: − «Харьков является первой столицей Украины»;− «Харьков − красивый город».

Составное высказывание, определяющее конъюнкцию, будет иметь вид: − «Харьков является первой столицей Украины и Харьков − красивый город».

Определение.

Высказывание , называемоедизъюнкцией и, ложно тогда и только тогда, когда ложны оба высказыванияи.

Эта логическая операция соответствует соединению высказываний естественного языка с помощью связки «или», употребляемой в смысле «не исключающее или»: «верно» , или верно, или оба высказывания равны.

Пример. Пусть имеем два атома: − «» и− «». Тогда высказывание «или» будет соответствовать формуле.

Определение.

Высказывание , называемоеимпликацией (условным предложением), ложно тогда и только тогда, когда истинно, аложно.

В импликации высказываниеназываетсяпосылкой (условием, антецедентом), а  следствием (заключением, консеквентом). Выражаемая импликацией причинно-следственная связь между ина естественном языке описывается следующими оборотами: «влечет», «если, то», «является достаточным основанием для», «, потому что», «при условии выполнения». Используемые в точных науках понятия достаточного и необходимого условий можно формально выразить с помощью импликации.

Пример.

Пусть имеем два атома: − «− простое» и− «− нечетное». Тогда высказывание «Для того, чтобыбыло нечетным, достаточно, чтобыбыло простым» будет соответствовать формуле.

Определение.

Если и высказывания, то высказывание , называемоеэквиваленцией, истинно тогда и только тогда, когда илибо оба истинны, либо оба ложны.

Эта операция в естественном языке соответствует оборотам: «… тогда и только тогда, когда …», «для того чтобы …, необходимо и достаточно …»,

Пример.

Пусть имеем два атома: − «идет дождь» и− «на небе тучи». Тогда высказывание «Дождь идет тогда и только тогда, когда на небе тучи» будет соответствовать формуле.

Алфавит логики высказываний содержит следующие символы:

1. высказывательные переменные или заглавные буквы с индексами;

2. логические символы (связки) ;

3. символы скобок ( ) и запятую.

Связки могут быть бинарными и унарными. Операции являются бинарными логическими связками, операция− унарной логической связкой.

При записи формул можно обойтись без некоторых скобок, если приписать ранги логическим связкам. Ранги логических связок чаще всего задаются в таком порядке (от высшего к низшему): .

Пример. − «Влажность большая»;− «Температура высокая»;− «Мы чувствуем себя хорошо».

Высказывание «Если влажность большая и температура высокая, то мы не чувствуем себя хорошо» можно записать в виде формулы или с учетом рангов операций.

Определение. В логике высказываний правильно построенная формула определяется рекурсивно следующим образом:

1. Атом есть формула.

2. Если и формулы, то  также формулы.

3. Никаких формул, кроме порожденных указанными выше правилами, не существует.

10.3 Алгебра логики и логика высказываний

Определение.

Логика высказываний – это алгебраическая структура ) с носителем – двоичным множеством {: «Ложь»,: «Истина»}, операциями (логическими связками): «» – конъюнкция, «» – дизъюнкция, «» – отрицание, «» – импликация, «~» – эквивалентность.

Если рассмотреть две алгебры: алгебру логики и алгебру логики высказываний, то они будут изоморфны друг другу, так как можно поставить взаимно однозначное соответствие между множествами,, а операции просто одинаковы. Если алгебры изоморфны, то элементы и операцииможно переименовать так, чтосовпадает с.Из условия изоморфности следует, что любое эквивалентное соответствие в алгебре сохраняется в. То есть соотношения, полученные в алгебре, автоматически распространяются на алгебру.

С логической точки зрения двоичные объекты, которые рассматривались в разделе «Элементы математической логики. Алгебра булевых функций»,  это высказывания, которые могут быть истинными или ложными. Формулы  это составные высказывания, истинность которых определяется истинностью входящих в них элементарных высказываний (обозначаемых буквами) и логическими операциями над высказываниями.

Поэтому все утверждения относительно алгебры логики справедливы и для алгебры логики высказываний.

Если рассматривать формулы, содержащие только логические операции , то в логике высказываний выполняется закон двойственности. Кроме того, формулы логики высказываний можно представить в виде ДНФ и КНФ, СДНФ и СКНФ (учитывая изоморфизм алгебр).

10.4 Интерпретация формул логики высказываний. Правильные рассуждения

Определение.

Приписывание истинностных значений атомам, из которых построено высказывание, называется интерпретацией высказывания.

Для высказывания, содержащего атомов, можно составитьинтерпретаций, так же, как и для-местной булевой функции.

Формулы логики высказываний можно задавать таблицами истинности, подобно булевым функциям.

Пример.

Рассмотрим таблицу истинности для логических связок логики высказываний (таблица 10.2)

Таблица 10.2  Таблица истинности логических связок

Л	Л	И	Л	Л	И	И
Л	И	И	Л	И	И	Л
И	Л	Л	Л	И	Л	Л
И	И	Л	И	И	И	И

Исходя из принимаемых формулами логики высказываний истинностных значений, формулы разделяются на тождественно истинные, тождественно ложные и необщезначимые.

Определение.

Формула называется тождественно истинной (тавтологией или общезначимой), если она принимает значение «истина» на всех интерпретациях (наборах значений переменных).

Определение.

Формула называется тождественно ложной (противоречивой или невыполнимой), если она принимает значение «ложь» на всех интерпретациях.

Определение.

Формула называется необщезначимой или непротиворечивой, если она на одних интерпретациях принимает значение «истина», а на других – «ложь».

Определение.

Все формулы, не относящиеся к противоречивым, образуют множество выполнимых формул.

Пример.

Формула − тавтология; формулаявляется противоречивой; формулаявляется выполнимой.

Перечислим наиболее важные тавтологии, предполагая, что − произвольные формулы:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. (закон Пирса).

При доказательстве утверждений различных математических теорий обычно используют рассуждения, которые на языке логики можно выразить формулами.

Определение.

Рассуждение называется правильным, если оно выражается тождественно истинной формулой.

Таким образом, проверить правильность рассуждения можно, построив соответствующую ему формулу и определив, является ли она тождественно истинной.

Доказать, что формула является тавтологией, можно следующими способами:

1. Построить таблицу истинности этой формулы. Если в таблице истинности на всех интерпретациях функция принимает значение «истина», то соответствующее формуле рассуждение является тавтологией.

2. Применив тождественные преобразования, привести её к виду одного из логических законов. Если в результате преобразований получим значение «истина», то формула является тавтологией.

10.5 Логическая эквивалентность и логическое следствие

Определение.

Две формулы называются равносильными, если на всех наборах значений входящих в них переменных эти формулы принимают одинаковые значения.

Равносильность формул логики высказываний вытекает из тождественности соответствующих формул алгебры логики. Равносильности формул ибудем обозначать через. Легко видеть, что равносильность − это отношение эквивалентности (оно рефлексивно, симметрично и транзитивно), поэтому равносильность называют такжелогической эквивалентностью.

Теорема.

Если − любые формулы, то имеют место следующие логические эквивалентности:

1. ,(коммутативность).

2. ,(ассоциативность).

3. ,

(дистирибутивность).

4. ,(идемпотентность).

5. ,(законы поглощения).

6. (закон двойного отрицания.)

7. ,(законы де Моргана).

8. ,.

9. ,.

10. ,.

Кроме того, с помощью отношения равносильности выражаются различные связки между формулами: ,,,,,,.

Любая из равносильностей может быть доказана с помощью таблиц истинности (а также следует из изоморфизма алгебр и).

Рассмотренные и подобные им равносильные соотношения можно использовать для преобразования и упрощения структуры сложного высказывания.

Определение. Высказывание являетсялогическим следствием высказывания , если формулаявляется тождественно истинной.

Данное определение может быть обобщено на случай произвольного числа посылок.

Определение. Высказывание являетсялогическим следствием высказываний , если− тождественно истинная формула.

Пример. Показать, что высказывание является логическим следованием высказывания.

Покажем, что формула является общезначимой. Для этого используем тождества логики высказываний для эквивалентных преобразований, учитывая, что:

.

Общезначимость формулы доказана.

10.6 Контрольные вопросы и задания

1. Какой вид предложений моделирует формальная логика?

2. Дайте определение понятию высказывание.

3. Дайте определение понятию алгебры логики высказываний.

4. Какие высказывания называются атомами?

5. Что в логике высказываний называют логическими связками?

6. Что в логике высказываний называют молекулами?

7. Дайте характеристику алфавита логики высказываний.

8. Что подразумевают в логике высказываний под правильно построенной формулой?

9. Дайте определение логического следствия одного (нескольких) высказываний.

10. Покажите, что алгебра логики и логика высказываний являются изоморфными.

11. Какие формулы можно получить, исходя из принимаемых формулами логики высказываний истинностных значений?

12. Какое рассуждение называется правильным?

13. Перечислите наиболее важные тавтологии.

14. Какие формулы называются равносильными? Приведите примеры равносильных формул.

Лекция 11. Исчисление высказываний

11.1 Основные понятия исчисления высказываний

Рассмотренное содержательное описание логики высказываний позволяет ответить на многие вопросы данной логики (например, является ли формула тавтологией, равносильны ли две заданные формулы и т.д.), используя таблицы истинности либо эквивалентные преобразования формул. Однако для ответа на более сложные вопросы используется другой метод − метод формальных аксиоматических теорий.

Исчисление высказываний, являясь формальной системой, представляет собой пример аксиоматической теории и один из возможных способов формализации логики высказываний. В исчислении высказываний особое внимание уделяется тождественно истинным высказываниям, поскольку они должны входить в любую теорию в качестве общелогических законов. Их порождение и является основной задачей исчисления высказываний. Данная формальная система позволяет проверить, является ли заданная формула тавтологией, а также получить общезначимые формулы логики высказываний.

Исчисление высказываний содержит язык, систему аксиом и правила вывода.

Рассмотрим каждое из этих составляющих.

Определение. Язык исчисления высказываний, являясь формальным языком для математических рассуждений, состоит из формул логики высказываний, правильно построенных с использованием алфавита данной логики.

Пример. Правильно построенные формулы с использованием алфавита логики высказываний: ,.Выражения, не являющиеся формулами: ,,.

11.2 Аксиомы и полнота исчисления логики высказываний

В математике и «чистой» логике доказывают теоремы, т.е. выводят следствия из определенных допущений, которые называются аксиомами или гипотезами. При этом предполагается, что они (аксиомы или гипотезы) тождественно истинны во всей рассматриваемой теории.

Определение.

Аксиомами логики высказываний является некоторое множество общезначимых формул логики высказываний.

Аксиомы (гипотезы) представляют собой перечень одного или более высказываний (посылок), которые часто называются схемами аксиом.

Системы аксиом исчисления высказываний подбираются таким образом, чтобы исчисление обладало свойством полноты.

Полнота исчисления высказываний заключается в том, что в данной системе имеется достаточное количество аксиом для того, чтобы вывести любую формулу логики высказываний, которая является тождественно истинной.

11.3 Выводимость в исчислении высказываний

Определение.

Выводом в исчислении высказывания называется всякая последовательность формул такая, что для любогоформулаесть либо аксиома, исчисления высказываний, либо непосредственное следствие каких-либо предыдущих формул, полученных по правилу вывода.

Определение.

Формула называетсятеоремой исчисления высказывания (как аксиоматической теории), если в ней существует вывод, в котором последней формулой является . Этот вывод называетсявыводом формулы .

Определение.

Формула называетсяследствием множества формул тогда и только тогда, когда существует такая последовательность формул, чтоесть, и для любогоформулаесть либо аксиома, либо формула из, либо непосредственное следование некоторых предыдущих формул. Эта последовательность называетсявыводом из. Элементы называютсяпосылками вывода или гипотезами.

Сокращенно можно записать так: (есть следствие). Если множествосостоит из формул, то пишут.

Правила вывода позволяют получать новые формулы, которые являются истинными при условии истинности всех посылок, входящих в правило.

В логике правила вывода используются, чтобы выводить одни истинные предложения из других истинных предложений.

Доказательство в исчислении высказываний представляет собой логический вывод списка высказываний.

Определение.

Дедуктивным выводом называется вывод формулы из формулы, основанный на том, чтоявляется логическим следствием.

Правила для дедуктивного вывода строятся на основе общезначимых формул логики высказываний вида . Эти правила часто записывают как правила формального вывода в следующем виде, где посылки вывода, а следствие (заключение). Тавтология, соответствующая такому правилу, это .

Пример.

Рассуждение по схеме не правильное рассуждение, так как формулане является тавтологией. Например, пусть: «5 − простое число» и: «5 − нечетное число»,: «Если 5 − простое число, то 5 − нечетное число» и: «5 − нечетное число», то: «5 − простое число», не правильное рассуждение.

Наиболее часто в практических задачах используются:

а) правило отделения;

б) правило подстановки.

Правило отделения имеет следующий логический смысл: если посылка верна, то верно и следствие из неё.

Пример.

Рассуждения с помощью правила отделения:

«Если студент не выучил теорию, то он не выполнит задание. Студент не выучил теорию. Следовательно, студент не выполнит задание».

«Если студент получил пять, значит, он решил задачу. Студент получил пять. Следовательно студент решил задачу».

Правило подстановки выражает тот факт, что если в тождественно истинной формуле все вхождения какого-либо атома заменить на некоторую формулу, то полученное выражение останется тождественно истинным.

Рассмотрим правило подстановки. Пусть и− формулы логики высказываний,− атомарная формула. Если− формула, выводимая в исчислении высказываний, содержащая атом, то− выводимая формула, полученная заменой всех вхожденийв формулена формулу. Правило подстановки записывается следующим образом:.

Пример.

Используя правило подстановки и коммутативный закон для дизъюнкции, доказать общезначимость следующей формулы: .

Запишем тождество, соответствующее коммутативному закону длдя дизъюнкции: . Определим подстановку − атомарную формулузаменим на:. Если опустить скобки в соответствии с приоритетом операций, то можно убедиться в истинности исходной формулы.

Кроме рассмотренных правил вывода в исчислении высказываний часто используются правила дедуктивного вывода, представленные в табл. 11.1.

Таблица 11.1 − Правила дедуктивных выводов логики высказываний

Правило дедуктивного вывода	Тавтология	Название правила
		Правило введения дизъюнкции
,		Правило введения конъюнкции
,		Правило удаления дизъюнкции (дизъюнктивный силлогизм)
		Правило удаления конъюнкции
		Правило контрапозиции импликации
,		Правило отделения (Modus Ponens)
,		Отрицательная форма правила отделения (ModusTollens)
,		Гипотетический силлогизм

11.4 Непротиворечивость, независимость

Проблема непротиворечивости возникает при рассмотрении любого исчисления (это одна из кардинальных проблем математической логики).

Определение.

Логическое исчисление непротиворечиво, если в нем не выводимы никакие две формулы, из которых одна является отрицанием другой.

Непротиворечивое исчисление − это такое исчисление, что, какова бы ни была формула , никогда формулыине могут быть одновременно выведены из аксиом этого исчисления с помощью указанных в нем правил.

Если в системе обнаруживаются выводимые формулы вида ито такое исчисление называется непротиворечивым. Такие исчисления никакой ценности не представляют, т.к. они не могут отражать в себе различие между истиной и ложью.

Теорема.

Исчисление высказываний непротиворечиво.

Рассмотрим свойство независимости системы аксиом исчисления высказываний.

Определение.

Если ни одну из аксиом системы исчисления высказываний нельзя вывести из остальных, применяя правила вывода данной системы, то говорят, что система аксиом независима.

Аксиомы исчисления высказываний подбираются таким образом, чтобы они были независимы.

11.5 Различные аксиоматизации исчисления высказываний

Существуют различные аксиоматизации исчисления высказываний, т.е. исчисление высказываний можно описать различными системами аксиом, используя различные наборы символов алфавита, лишь бы с их помощью можно было выразить все остальные логические операции.

Пример.

1. Аксиоматизация исчисления высказывания Гилберта и Аккермана (1938):

а) связки ;

б) аксиомы:

,

,

,

;

в) правило: Modus Ponens (правило отделения).

2. Аксиоматизация исчисления высказывания Россера (1953):

а) связки ;

б) аксиомы:

,

,

;

в) правило: Modus Ponens (правило отделения).

3. Аксиоматизация исчисления высказывания Клини (1952)

а) связки ;

б) аксиомы:

,

,

,

,

,

,

,

,

,

.

в) правило: Modus Ponens (правило отделения).

Приведем в качестве примера следующую формальную систему исчисления высказывания:

1. Язык системы состоит из правильно построенных формул логики высказываний, содержащих операции. Алфавит языка совпадает с алфавитом логики высказываний и содержит, кроме символов перечисленных логических операций, символы скобок и символы для обозначения высказываний.

2. Аксиомы системы :

а) ;

б) ;

в) .

3. Правила вывода:

а) правило отделения (Modus Ponens);

б) правило подстановки.

Достоинством данной формальной системы является лаконичность при сохранении определенной наглядности.

11.6 Некоторые приемы доказательств в исчислении высказываний

Для доказательства истинности утверждений в исчислении высказываний существуют определенные приемы. Один из них использует теорему о дедукции.

Теорема о дедукции.

Пусть − множество формул,− формулы и. Тогда.

Эта теорема обосновывает следующий прием: в математических рассуждениях часто какое-то утверждение доказывают в предположении некоторого другого утверждения, после чего заключают, что верно утверждение «еслито».

Вместо прямого логического вывода формулы из формулычасто оказывается удобным доказать противоречивость формулытем самым доказав истинность формулы. Такой метод (прием) доказательства называется методом от противного и может быть реализован следующими схемами:

1) − если из предположения, что− верно, а− неверно, следует два противоречащих друг другу высказываний, то это означает, что изследует;

2) − если из предположения, что− неверно, следует, чтоневерно, то это означает, что изследует.

11.7 Контрольные вопросы и задания

1. Что представляет собой исчисление высказываний?

2. Поясните понятия языка, аксиом и правил вывода исчисления высказываний.

3. Приведите примеры аксиом исчисления высказываний.

4. Каким образом строится дедуктивный вывод?

5. Дайте краткую характеристику основных правил дедуктивного вывода.

6. Перечислите правила дедуктивных выводов логики высказываний.

7. В чем состоит полнота и непротиворечивость исчисления высказываний?

8. Дайте определение независимой системы аксиом.

9. Сформулируйте теорему дедукции.

10. В чем заключается метод доказательства от противного?

Лекция 12. Логика предикатов (логика первого порядка). Предикаты. Алгебра предикатов

12.1 Основные понятия логики предикатов

Логика высказываний, рассмотренная выше, является достаточно узкой логической системой, в ней не все логические рассуждения могут быть осуществлены. Например, в рамках этой системы нельзя записать такое рассуждение «Простое число 2 − четное. Следовательно, существуют простые четные числа».

Многие утверждения, имеющие форму высказываний, на самом деле таковыми не являются, так как содержат переменные, конкретные значения которых не указаны. Поскольку такое утверждение при одних значениях переменных может быть истинным, а при других – ложным, ему не может быть предписано истинностное значение. Такие утверждения называются предикатами. В логику предикатов также введены дополнительные, новые по сравнению с логикой высказываний, логические понятия, а именно, предикат, терм, квантор.

Определение.

Предикатом называется функция , переменные которой принимают значения из некоторого множества, а сама она принимает два значения(истинное) и(ложное), т.е.(где).

Понятие предиката является частным случаем понятия функции, для которой четко фиксирована область значений.

Предикаты становятся высказываниями, когда их переменным присваиваются значения.

Пример.

Предикатами являются следующие утверждения:

Пусть , тогда утверждениеявляется высказыванием, и это высказывание истинно. Приутверждениетоже является высказыванием, и это высказывание ложно.

Определение.

Множество значений , которое может принимать, называетсяуниверсом или предметной областью.

Пример.

В частности, предметной областью может являться множество действительных чисел, множество целых чисел или другие подобные множества.

Множество значений перменных определяется обычно математическим контекстом.

Определение.

В общем случае определен некоторый предикат, если:

1) задано некоторое (произвольное) множество, называемое областью определения предиката (предметная область);

2) фиксировано множество {И, Л}, называемое областью значений;

3) указано правило, с помощью которого каждому элементу, взятому из предметной области, ставится в соответствие один из двух элементов из области значений.

Определение.

Предикат с одной переменной называется одноместным предикатом и может обозначаться, например, , где− переменная. Предикат, имеющий две переменные, называется двухместным предикатом и может обозначаться, например, , где− переменные, а предикат, содержащий переменных (аргументов), называется -местным предикатом и обозначается . Высказывания считаютсянульместным предикатом.

Количество аргументов предиката называется егопорядком.

Пример.

Высказывание «− действительное число» можно представить одноместным предикатом, «меньше» − двуместным предикатом. Еслиизамещены конкретными значениями (объектами), то предикат переходит в высказывание, которое рассматривается как нульместный предикат.

Определение.

Аргументы предиката называются термами. Термы-константы и термы-переменные называются предметными константами и предметными переменными.

Предикаты обычно обозначаются большими латинскими буквами. Иногда бывает удобно указывать число переменных у предиката путем введения верхнего индекса, например является-местным предикатом.

Предикатом чаще всего обозначают свойство или действие, выраженное в высказывании сказуемым, а объекты и субъекты этого действия, а также другие члены предложения являются аргументами данного предиката. В качестве обозначения предиката также можно выбрать слово, отражающее его смысловое значение.

Пример.

Представим в виде предиката высказывания: «делится на 7», «делится на», «− простое число». Выберем в качестве названий предикатов действия или свойства данных предложений: ДЕЛИТСЯ, ПРОСТОЕ. Тогда заданные высказывания можно записать в виде предикатов следующим образом: ДЕЛИТСЯ(,7), ДЕЛИТСЯ(,), ПРОСТОЕ(). Здесь первый и третий предикат являются одноместными и каждый выражает некоторое свойство числа ; второй предикат – двуместный и выражает бинарное отношение делимости на множестве чисел.

Для построения атомов логики предикатов разрешается использовать следующие типы символов:

• индивидуальные символы или константы, которые обычно являются именами объектов, например: Сократ, 13;

• символы предметных переменных, в качестве которых обычно выступают буквы латинского алфавита, возможно, с индексами, например: ;

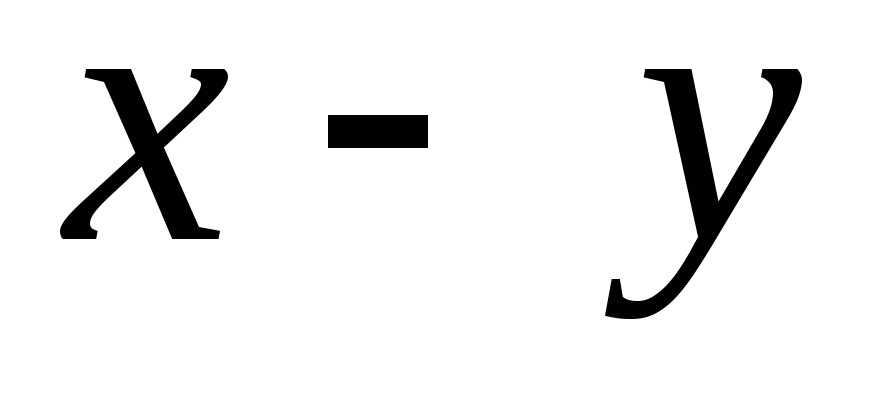• функциональные символы – строчные буквы латинского алфавита или осмысленные слова из строчных букв, например: минус() – функциональный символ «», отец () – функциональный символ «отец человека »;

• предикаты – прописные буквы или осмысленные слова из прописных букв, например: ,, ДЕЛИТСЯ, БОЛЬШЕ, ПРОСТОЕ.

Пример.

Переведем на естественный язык следующие высказывания логики предикатов: 1) РАВНЯТЬСЯ; 2) ЗНАТЬ(папа(Вася), математика).

Предикат РАВНЯТЬСЯсоответствует утверждению «равняется 5» естественного языка. Здесь 5 – константа, − предметная переменная.

В высказывании ЗНАТЬ(папа(Вася), математика) функциональный символ «папа()» принимает значение из множества людей, соответствующее отношению «быть отцом ». Поэтому выражение папа(Вася) следует интерпретировать как «Васин папа». Таким образом, предикат ЗНАТЬ (папа(Вася), математика) соответствует предложению «папа у Васи знает математику» естественного языка. Здесь «Вася» и «математика» являются константами, а − предикатная переменная.

12.2 Операции логики предикатов. Кванторные операции

Над предикатами можно производить обычные логические операции, которые обозначаются символами и называются логическими связками (как и в логике высказываний).

Пример.

Пусть − предикат «делится на 3»,− предикат «делится на 5», тогда выражениеозначает «делится на 3 и делится на 5», т.е. определяет предикат делимости на 15.

Кроме операций логики высказываний к предикатам применяются операции связывания квантором. Кванторы управляют областью значения переменной, следующей за символом квантора.

Определение.

Пусть − предикат, определенный на множестве. Высказывание «для всехистинно» обозначается.

Определение.

Символ называетсяквантором всеобщности (квантором общности).

Если применяется квантор всеобщности, то говорится, что высказывание истинно для всех из некоторого множества.

Определение.

Высказывание «существует такой , чтоистинно» обозначается, где символназываетсяквантором существования.

Квантор существования применяется, когда нужно указать, что существует хотя бы одно значение переменной, для которой истинно данное высказывание.

Пример. Запишем в виде предикатов с кванторами следующие высказывания: «Все студенты сдают экзамены», «Некоторые студенты сдают экзамены на отлично».

Введем предикаты: − «сдавать экзамены» и− «сдавать экзамены на отлично». Предметная область данных предикатов представляет собой множество студентов. Тогда исходные выражения примут вид:и.

Заметим, что имеют место ранги логических связок, учитывая которые кванторы иразмещаются между связкамии.

Применение кванторов к многоместным предикатам уменьшает количество переменных, от которых зависит данный предикат. Например, применение квантора по одной из переменных двухместного предиката превращает его в одноместный.

Квантор общности можно истолковывать как обобщение конъюнкции, а квантор существования – как обобщение дизъюнкции, т.е. если область определения предикатаконечна, например,, то высказываниеэквивалентно, а высказывание− дизъюнкции.

Пример.

Пусть задан предикат , который означает «− нечетное число» и определен на области.

Высказывание означает: «− нечетное число», и− нечетное число и− нечетное число», а высказываниеозначает то же, что и дизъюнкция «− нечетное число, или− нечетное число, илинечетное число»

12.3 Формулы и их интерпретация в логике предикатов

На языке предикатов можно составить гораздо более сложные предложения, чем на языке высказываний. Определим понятие формулы в логике предикатов.

Алфавит логики предикатов в общем случае содержит следующие символы:

1. символы предметных переменных: ;

2. символы предикатов: , где;

3. логические символы: ;

4. символы кванторов: ;

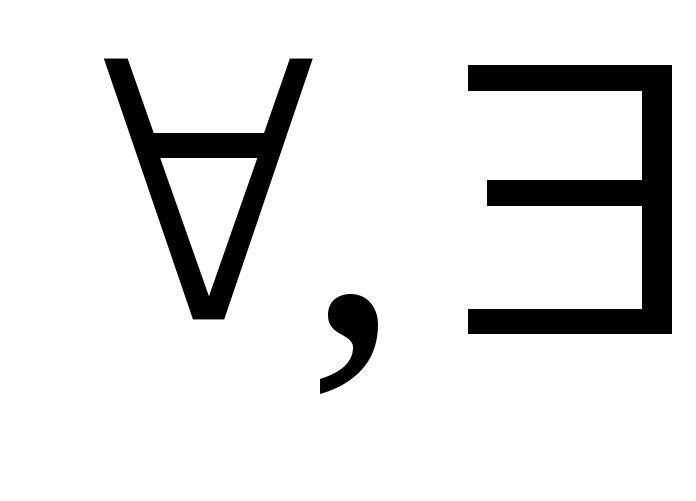5. скобки и запятую: ),( .

Определение.

Если  -местный предикат и термы, то называетсяатомом или элементарной формулой логики предикатов.

Пример.

Атомами являются: ДЕЛИТСЯ(,13), ДЕЛИТСЯ(,), БОЛЬШЕ (плюс(,1),), РАВНЯТЬСЯ(,1), СДАВАТЬ(студенты, сессия).

Определение.

Правильно построенными формулами логики предикатов называются формулы, которые можно рекурсивно определить следующим образом:

1. Атом является формулой.

2. Если и− формулы, тотакже являются формулами.

3. Если − формула, а− свободная переменная, тои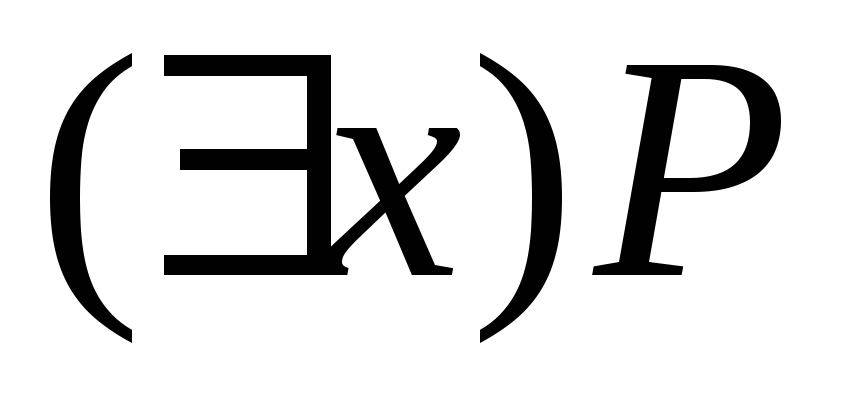тоже формулы.

4. Никаких формул, кроме порожденных указанными выше правилами, не существует.

Введем понятие свободного и связанного вхождения переменной в формулу.

Определение.

В выражениях иформула, на которую распространяется действие квантора, называетсяобластью действия квантора.

Следует заметить, что формула может и не иметь вхождений переменной. В таком случае считается, что формулыиодинаковые.

Определение.

Вхождение переменной в формулуназываетсясвязанным, если − переменная квантораили, входящего в данную формулу, либо находится в области действия квантораили, входящего в данную формулу. В противоположном случае вхождение переменнойв данную формулу называетсясвободным.

Пример.

Определим вхождение переменных в следующие формулы: а) ; б), в).

Единственное вхождение переменной в формулу а) является свободным. Первое вхождение переменнойв формулу б) свободное, а второе и третье − связанные. Все вхождения переменнойв формулу в) связанные.

Определение.

Переход от килиназываетсясвязыванием переменной , а сама переменнаяв этом случае –связанной. Переменная, не связанная никаким квантором, называется свободной.

Смысл связанных и свободных переменных в предикатных выражениях различен. Свободная переменная − это обычная переменная, которая может принимать различные значения из ; выражение– переменное высказывание, зависящее от значения. Выражениене зависит от переменнойи при фиксированныхиимеет вполне определенное значение. Это в частности означает, что переименование связанной переменной, т.е. переход отк, не меняет истинности выражения.

Определение. Формула называется замкнутой, если она не имеет свободных переменных.

Поскольку действие квантора может распространяться не на всю формулу, а только на её часть, то переменная может быть связанной в одной части формулы и свободной в другой. В этом случае полагают, что переменная является и связанной, и свободной одновременно.

Чтобы предикат был высказыванием, все его переменные должны иметь конкретные значения или быть связаны соответствующим квантором.

Пример. не является высказыванием, так как переменнаяне связана никаким квантором.

Формулы имеют смысл только тогда, когда существует какая-либо интерпретация символов, входящих в эти формулы.

Определение.

Интерпретация формулы логики предикатов состоит из элементов непустой предметной области , значений всех констант, функциональных символов и предикатов, встречающихся в. Указанные значения задаются следующим образом:

1. Каждой константе ставится в соответствие некоторый элемент из .

2. Каждому -местному функциональному символу ставится в соответствие отображение изв. Здесь, где.

3. Каждому -местному предикату ставится в соответствие отображение изв {И, Л}.

Для каждой интерпретации на области формула может получать истинностное значение И или Л согласно следующим правилам:

1. Если заданы значения формул и, то истинностные значения формул (), (), (),(),() получаются с помощью таблиц истинности соответствующих логических операций.

2. Формула получает значение И, еслиполучает значение И для каждогоиз, в противном случае она получает значение Л.

3. Формула получает значение И, еслиполучает значение И хотя бы для одногоиз, в противном случае она получает значение Л.

4. Формула, содержащая свободные переменные, не может получать истинностные значения.

Пример. Пусть задан предикат . Формулане истинна, если универсом (предметной областью) является множество целых чисел, однако она была бы истинной, если в качестве предметной области взять множество целых чисел, больших чем 2.

Квантифицированный предикат , где, не является истинным, если предметная область − множество целых чисел, потому что имеются значенияиз этой области (например,) такие, чтоложно. Для истинностидолжно быть истинным для каждого значенияиз предметной области.

Пример. Предикат , где, является истинным, если предметной областью есть множество действительных чисел, т.к.истинно для.

Предикат , где, также истинен, если предметной областью есть множество действительных чисел, однако, он не является истинным, если предметная область есть множество целых чисел, т.к. не существует целого числа, квадрат которого равен 5.

При логической (истинностной) интерпретации формул логики предикатов так же, как и в логике высказываний определяются общезначимые, противоречивые, выполнимые, необщезначимые формулы, а также логическое следствие.

12.4 Законы и тождества логики предикатов

Все законы и тождества, которые справедливы в логике высказываний, остаются справедливыми и в логике предикатов.

Для эквивалентных преобразований предикатных высказываний с кванторами дополнительно необходимо использовать приведенные ниже законы.

1. Замена связанной переменной:

;

,

−одноместный предикат.

Введение нового обозначения связанной переменной (т.е. переименование связанной переменной) не изменяет смысл формулы логики предикатов, если выполняется следующее условие: никакая свободная переменная в любой части формулы не должна после переименования оказаться связанной.

Пример.

Для нового обозначения связанной переменной следует выбирать букву, которая отсутствует в формуле, например, . Здесь осуществлена операция переименования связанной переменной.