19

СТА: Лекция №6 - Хэш-таблицы

Версия 2.0, 17 сентября 2013г.

(С) 2012-2013, Зайченко Сергей Александрович, к.т.н, ХНУРЭ, доцент кафедры АПВТ

Мотивация

Практическое применение алгоритмов поиска с линейной вычислительной сложностью весьма ограничено. Фактически, линейный поиск пригоден лишь для обработки очень малых объемов данных, поскольку в худшем случае для N хранимых элементов выполняется N сравнений ключей. Если число элементов не превышает 10, использование для поиска таких простых структур данных, как массив или связный список, может быть оправдано минимумом служебных вычислений, необходимых для функционирования, а также простотой реализации.

Алгоритм бинарного поиска существенно более эффективен, однако требует наличия заранее упорядоченных данных. В общем случае, реальные данные не будут упорядочены, а время их сортировки может существенно превысить приемлемые для задачи пороговые значения.

Если число элементов превышает 10, о характере хранимых данных-ключей неизвестно никакой дополнительной информации, ключи не упорядочены ни по какому критерию, то необходимо задуматься об использовании более сложной структуры данных для реализации отображений и множеств. Одной из таких структур являются хэш-таблицы.

Как будет показано далее, реализация отображений и множеств на основе хэш-таблиц значительно сложнее реализации на основе массивов или связных списков. Также, хэш-таблицы требуют существенно большего объема памяти для функционирования, а в процессе поиска выполняют большее число служебных действий для обеспечения своей работы. Если речь идет о малом количестве элементов, применение такой структуры данных может быть нерациональным как с точки зрения памяти, так и времени. Однако, для больших отображений и множеств все усилия полностью окупаются значительно лучшей эффективностью - в среднем, время поиска ключа в хэш-таблице вообще не зависит от количества хранимых ключей (O(1) - константная вычислительная сложность). При грамотной реализации, производительность поиска в хэш-таблице на большом количестве ключей (тысячи, десятки тысяч и более) будет предпочтительнее бинарного поиска, при этом не потребуется предварительного упорядочивания.

Константной вычислительной сложностью O(1) также обладает случай реализации отображений и множеств, в котором ключи ставятся в прямое соответствие с индексами массива. Однако, в общем случае, пространство всех возможных ключей может быть слишком большим, например, весь возможный диапазон числа типа int. Чтобы выделить для каждого возможного ключа по ячейке потребуется очень большой объем памяти. Даже если предположить, что среда выполнения имеет доступ к огромным объемам оперативной памяти, большая часть ячеек в таком массиве бы не использовалась, и память расходовалась бы напрасно.

Устройство хэш-таблицы

Предположим, имеется большое множество теоретически возможных ключей, состоящее из B элементов. Также, предположим имеется массив из N ячеек, при этом N несравнимо меньше чем B. Для организации хэш-таблицы необходимо подобрать некоторую функцию называемую ХЭШ-ФУНКЦИЕЙ, принимающую любой из ключей , и возвращающую целое неотрицательное число , называемое ХЭШ-КОДОМ. Не имеет определяющего значения конкретная форма и сложность функции , при условии, что она обладает следующими свойствами:

1. Функция не имеет состояния и всегда возвращает для одинаковых ключей одинаковый результат, сколько бы раз функция не вызывалась:

.

2. Область значений функции распределяется приблизительно равномерно для всех возможных ключей. Т.е. для каждого хэш-кода существует приблизительно одинаковое количество ключей , хэш-код которых равен .

В идеальном случае, для каждого допустимого значения хэш-кода будет существовать ключей-аргументов, т.е. все ключи будут равномерно распределены по возможным хэш-кодам. Очевидно, идеальные случаи на практике встречаются редко, и хэш-функции не дают абсолютно равномерного распределения ключей по значениям. Если распределение достаточно равномерно, то и хэш-таблицы будут функционировать достаточно эффективно.

Например, пусть ключи x являются целыми числами, которые могут принимать любые значения в допустимом диапазоне типа int (от -2³¹ до 2³¹-1), т.е. B=2³². Очевидно, массив такого размера создавать непрактично даже на очень мощном компьютере, поскольку это бы потребовало нескольких гигабайт оперативной памяти (B возможных значений ключа * размер хранимого значения). Простейшей хэш-функцией для такого типа ключа является остаток от деления:

Такая хэш-функция, несмотря на тривиальность, обладает обоими необходимыми свойствами - возвращает одинаковые результаты для одинаковых ключей и равномерно распределяет множество ключей-аргументов по области возможных значений.

Возьмем конкретный набор ключей и соответствующих им значений , где M - конечное число, сопоставимое с размером массива N, и несравнимо меньшее количества всех возможных ключей B. Для каждого ключа вычислим значение хэш-функции и получим набор хэш-кодов . Предположим, M<N, и все полученные хэш-коды являются уникальными между собой. Тогда представляется возможным свободно поместить все пары ключ-значение в массив A, называемый ХЭШ-ТАБЛИЦЕЙ, при этом пары ключ-значение попадут в ячейки, индекс которых соответствует хэш-коду ключа. Т.е. по индексу в массиве A, соответствующему хэш-коду конкретного ключа будет находится ячейка с парой ключ-значение :

.

Пусть N = 10, M = 5, и имеются следующие наборы ключей и соответствующих им значений:

x	y
25	315
37	210
13	150
20	242
18	167

Используя простейшую хэш-функцию для целых чисел - остаток от деления на N - получим для всех ключей следующие хэш-коды:

x	h(x)=x%N (N=10)
25	5
37	7
13	3
20	0
18	8

Разместим все пары в соответствующие ячейки массива и получим хэш-таблицу:

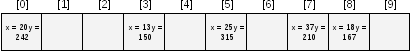
Теперь, для поиска в таблице значения по некоторому ключу необходимо:

1. Вычислить значение хэш-кода для ключа: .

2. Если ячейка по индексузанята, сравнить хранящийся в ней ключ с искомым , и если они равны, вернуть значение .

3. Если же ячейка по индексу не занята, или хранимый в этой ячейке ключ не равен , из этого следует, что искомый ключ в таблице не содержится.

Аналогичным образом должно реализовываться удаления пары ключ-значение по ключу :

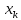1. Вычислить значение хэш-кода для ключа: .

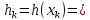
2. Если ячейка по индексузанята, сравнить хранящийся в ней ключ с искомым 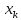, и если они равны, освободить ячейку.

3. Если же ячейка по индексу 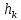не занята, или хранимый в этой ячейке ключ не равен , из этого следует, что искомый ключ в таблице не содержится, и был инициирован некорректный запрос на удаление незарегистрированного ключа.

Точно таким же образом, попытка вставить в хэш-таблицу новую пару , ключ которой уже представлен в таблице, будет легко обнаружена, поскольку вычисление хэш-кода от одинаковых ключей приведет к получению идентичных индексов в таблице. В этом случае, в зависимости от требований задачи, следует либо заблокировать вставку, либо перезаписать предыдущее значение, соответствующее данному ключу, на новое.