27 Ста: Лекция №8 - Бинарные деревья поиска

Версия 2.01, 12 декабря 2014г.

(С) 2012-2014, Зайченко Сергей Александрович, к.т.н, ХНУРЭ, доцент кафедры АПВТ

Характеристическое свойство bst

На основе бинарных деревьев представляется возможным эффективно реализовать АТД “Отображение” и “Множество”, при условии, что ключи могут быть упорядочены по оператору <. Этому условию удовлетворяют большинство используемых на практике типов данных ключей. Для чисел используется естественный смысл операции меньше, для строк - алфавитный порядок, для перечисляемых типов - порядок объявления меток. При необходимости, можно определить смысл операции < для массивов (по аналогии со строками) и структур (исходя из логики понятия).

Предположим, имеется неупорядоченный набор уникальных чисел:

5 2 7 3 9 0 1 4 6 8

Добавляя на каждом шаге числа при последовательном переборе, сформируем из данного набора бинарное дерево с узлами, метками которого являются эти числа, таким образом, что всегда будет соблюдаться следующее характеристическое свойство:

• любой ключ, находящийся в левом поддереве, меньше ключа в узле-родителе

• любой ключ, находящийся в правом поддереве, больше ключа в узле-родителе.

Если во входном наборе попадется повторяющееся число, его следует либо проигнорировать, либо следует сигнализировать внешней среде об ошибке.

Ниже в графической форме приведена пошаговая процедура добавления рассматриваемой последовательности чисел в дерево. Первое число 5 попадает в корневой узел:

Число 2 меньше числа 5, поэтому оно будет размещено в левом поддереве:

Число 7 больше числа 5, в связи с чем его следует поместить в правом поддереве:

В дальнейшем процедура будет выполняться рекурсивно. Следует сравнивать очередное входное число с текущим узлом-родителем, начиная от корня, и, если вставляемое в дерево новое число-ключ меньше числа в узле-родителе, новый узел должен вставляться в левое поддерево, а если больше - в правое. Число 3 меньше 5, значит следует двигаться по левому поддереву. Число 3 больше 2, соответственно, это число должно стать правым поддеревом для узла с числом 2:

Число 9 больше числа 5 и больше числа 7, его место в правом поддереве узла с числом 7:

Число 0 меньше числа 5 и меньше числа 2, его поместим в левом поддереве узла с числом 2:

Число 1 меньше числа 5, меньше числа 2, однако больше числа 0. Значит, у узла с числом 0 должно появиться правое поддерево:

Число 4 меньше числа 5, больше числа 2 и больше числа 3, соответственно такое число будет размещено в правом поддереве узла с числом 3:

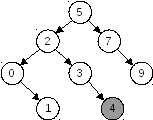
Число 6 больше числа 5, но меньше числа 7. Узел с числом 7 получит левое поддерево:

Число 8 больше 5, больше 7, но меньше 9, следовательно узел 9 получит левое поддерево:

Бинарные деревья, ключи в узлах которых упорядочены в соответствии с продемонстрированным выше характеристическим свойством, называются деревьями бинарного поиска (BST).