Сравнение простых алгоритмов сортировки

Рассмотренная ранее пузырьковая сортировка является примитивным методом и практически не имеет применения в реальном программном обеспечении, как обладающая довольно высокой квадратичной вычислительной сложностью.

Схожей вычислительной сложностью обладают еще два распространенных алгоритма - сортировка вставками (insertion sort) и сортировка выбором (selection sort):

void insertionSort ( int* _pData, const int _N )

{

for ( int i = 1; i < _N; i++ )

{

int j = i;

while ( j && ( _pData[ j ] < _pData[ j - 1 ] ) )

{

int temp = _pData[ j - 1 ];

_pData[ j - 1 ] = _pData[ j ];

_pData[ j ] = temp;

--j;

}

}

}

void selectionSort ( int* _pData, const int _N )

{

for ( int i = 0; i < _N - 1; i++ )

{

int lowIndex = i;

for ( int j = i + 1; j < _N; j++ )

if ( _pData[ j ] < _pData[ lowIndex ] )

lowIndex = j;

int temp = _pData[ lowIndex ];

_pData[ lowIndex ] = _pData[ i ];

_pData[ i ] = temp;

}

}

В среднем случае, когда начальный порядок сортируемых данных произволен, оба эти алгоритма также имеют квадратичную вычислительную сложность. Однако, их поведение существенно различается в лучшем и худшем случаях.

Когда на вход подается уже отсортированный массив, алгоритм сортировки вставками не делает ни одной перестановки данных, осуществляя при этом всего N-1 сравнение. Соответственно, в лучшем случае его вычислительная сложность стремится к линейной. Сортировка выбором таким интересным свойством не обладает, и для получения результата на отсортированном массиве сделает сравнений и N-1 перестановку.

Когда же на вход будет подан массив, отсортированный в обратном порядке, алгоритм сортировки вставками сделает по перестановок и сравнений, а алгоритм сортировки выбором сохранит свои свойства, осуществивсравнений и N-1 перестановку на любом входном наборе данных.

Таким образом, 3 простейших алгоритма сортировки - пузырьковая, вставками и выбором - имеют схожую вычислительную сложность в среднем и в худшем случаях, однако в лучшем случае алгоритм сортировки вставками наиболее эффективен. Схожая вычислительная сложность не означает, что все 3 алгоритма будут выполняться за одно и то же время, поскольку могут отличаться константные коэффициенты.

Ниже приведено сравнение замеров производительности трех рассмотренных алгоритмов сортировки для различных N в 3-х вариантах - случайные данные, отсортированные данные и данные, отсортированные в противоположном порядке. Разумеется, при выполнении на другом компьютере абсолютные значения времени могут существенно отличаться, однако пропорции между значениями должны сохраниться.

Время сортировки случайного набора данных (средний случай):

Количество данных	Пузырьковая	Вставками	Выбором
100 000	57.500s	33.781s	23.156
50 000	14.360s	8.406s	5.796s
20 000	2.296s	1.359s	0.921s
10 000	0.578s	0.343s	0.234s
5 000	0.141s	0.093s	0.062s

Время сортировки уже отсортированных данных (лучший случай):

Количество данных	Пузырьковая	Вставками	Выбором
100 000	23.156s	< 0.001s	23.140s
50 000	5.796s	< 0.001s	5.782s
20 000	0.922s	< 0.001s	0.938s
10 000	0.218s	< 0.001s	0.234s
5 000	0.063s	< 0.001s	0.063s

Время сортировки данных, отсортированных в обратном порядке (худший случай):

Количество данных	Пузырьковая	Вставками	Выбором
100 000	61.781	67.563s	24.157s
50 000	15.454s	16.906s	6.047s
20 000	2.469s	2.703s	0.953s
10 000	0.625s	0.672 s	0.235s
5 000	0.156s	0.157s	0.062s

Из полученных данных измерений можно сделать интересные выводы:

• Метод сортировки выбором в среднем является наиболее эффективным, кроме того его время выполнения стабильно на любом наборе поданных входных данных. Стабильное время выполнения - это важная характеристика алгоритма, когда о характере подаваемых данных заранее ничего не известно.

• Метод сортировки вставками существенно выигрывает у двух других при подаче уже отсортированного массива (фактически, время выполнения настолько малое, что его не удается замерить), однако заметно проигрывает сортировке выбором в худшем случае.

Сортировка слиянием

Сортировка слиянием является намного более эффективным алгоритмом сортировки по сравнению с ранее рассмотренными. Предположим, имеется случайный набор целых чисел, требующий сортировки:

Разобьем данный массив на две равные половины:

А затем каждую из половин разобьем еще надвое:

И т.д., пока не дойдет до массивов, состоящих не более чем из двух элементов:

Отсортировать такие массивы из двух элементов не составляет никакого труда - достаточно сравнить 2 числа и переставить их местами, если это необходимо:

Далее следует объединить (“слить”) соседние массивы таким образом, чтобы получить один вдвое больший отсортированный массив вместо двух. Поскольку две объединяемые части к этому моменту уже отсортированы, слияние осуществляется выбором наименьшего из значений в двух массивах при последовательном проходе:

Слияние следует повторить на следующем уровне:

И т.д, пока не будет получен отсортированный массив исходного размера:

Оценим вычислительную сложность данного алгоритма. В общем виде, алгоритм разбивает задачу на 2 подзадачи равного размера и вызывает для их обработки сам себя рекурсивно, а затем осуществляет процедуру слияния двух массивов в один больший. Т.е.:

Процедура слияния последовательно проходит два отсортированных массива-операнда, и, очевидно, обладает линейной вычислительной сложностью. Соответственно, рекуррентное соотношение выше имеет следующий вид:

Аналогично процессу раскрытия, предложенному при разъяснении алгоритма бинарного поиска, предположим, что существует некоторое число , такое что. Тогда:

Разделив левую и правую часть уравнения на , получим:

Поэтапно раскрывая рекурсию шаг за шагом, получим следующее соотношение:

Возвращаясь к оригинальному количеству элементов, получим линейно-логарифмическую вычислительную сложность, что существенно лучше квадратичной сложности предыдущих рассмотренных алгоритмов сортировки:

Если количество входных данных невелико, скажем, N<10, простейшие алгоритмы сортировки будут выполняться за меньшее время, чем алгоритм слияния, однако при возрастании N выигрыш слияния станет очевиден. Этот факт можно использовать для комбинирования алгоритмов. Если в результате разбиения исходного массива на одном из уровней получен массив с длиной до 10 элементов, можно применить другой алгоритм сортировки, например, сортировку выбором. Это позволит повысить производительность сортировки слиянием в целом.

Ниже представлена программная реализация данного подхода:

// Вспомогательная функция слияния двух отсортированных массивов в один

void mergeSorted ( const int * _pFirst, int _firstSize,

const int * _pSecond, int _secondSize,

int * _pTarget )

{

// Поддерживаем 3 текущих индекса:

// - индекс в целевом массиве (targetIndex)

// - индекс в первом массиве-операнде (firstIndex)

// - индекс во втором массиве-операнде (secondIndex)

// Проходим по массивам-операндам и формируем целевой массив

int firstIndex = 0, secondIndex = 0, targetIndex = 0;

while ( firstIndex < _firstSize && secondIndex < _secondSize )

{

// Если число из первого массива не больше числа из второго - оно идет первым

if ( _pFirst[ firstIndex ] <= _pSecond[ secondIndex ] )

{

_pTarget[ targetIndex ] = _pFirst[ firstIndex ];

++ firstIndex;

}

// Иначе берется число из второго массива

else

{

_pTarget[ targetIndex ] = _pSecond[ secondIndex ];

++ secondIndex;

}

++ targetIndex;

}

// Возможно второй массив был короче. Дописываем оставшиеся элементы 1-го в конец

if ( firstIndex < _firstSize )

memcpy( _pTarget + targetIndex, _pFirst + firstIndex, sizeof( int ) * ( _firstSize - firstIndex )

);

// Аналогично для случая, если первый массив был короче.

else if ( secondIndex < _secondSize )

memcpy( _pTarget + targetIndex, _pSecond + secondIndex, sizeof( int ) * ( _secondSize - secondIndex )

);

}

// Основная функция сортировки слиянием

void mergeSort ( int * _pData, int _N )

{

// Для малых N используем сортировку выбором

if ( _N < 10 )

selectionSort( _pData, _N );

else

{

// Вычислияем размеры половин (могут отличаться на 1 при нечетном N)

int halfSize = _N / 2;

int otherHalfSize = _N - halfSize;

// Формируем первую половину в дополнительном массиве N/2

int * pFirstHalf = new int[ halfSize ];

memcpy( pFirstHalf, _pData, sizeof( int ) * halfSize );

// Формируем вторую половину в дополнительном массиве N/2

int * pSecondHalf = new int[ otherHalfSize ];

memcpy( pSecondHalf, _pData + halfSize, sizeof( int ) * otherHalfSize );

// Сортируем половины рекурсивно

mergeSort( pFirstHalf, halfSize );

mergeSort( pSecondHalf, otherHalfSize );

// Осуществляем слияние отсортированных половин в единый массив

mergeSorted( pFirstHalf, halfSize, pSecondHalf, otherHalfSize, _pData );

// Освобождаем временные массивы

delete[] pFirstHalf;

delete[] pSecondHalf;

}

}

Ниже приведены результаты измерения производительности сортировки данной реализации, подтверждающие существенное превосходство над простейшими методами:

Размер массива	Случайные данные	Отсортированные данные	Данные в обратном порядке
500 000	0,235s	0,166s	0,172s
200 000	0,104s	0,073s	0,074s
100 000	0,050s	0,036s	0,036s
50 000	0,025s	0,017s	0,017s
20 000	0,012s	0,008s	0,008s
10 000	0,006s	0,004s	0,004s

Если отключить использование сортировки выбором для нижних уровней разбиения, а пользоваться идеей базового алгоритма, очевидно падение производительности, что подтверждает изначально выдвинутую гипотезу для малых N:

Размер массива	Случайные данные	Отсортированные данные	Данные в обратном порядке
500 000	0,520s	0,452s	0,458s
200 000	0,247s	0,221s	0,217s
100 000	0,121s	0,111s	0,108s
50 000	0,064s	0,055s	0,053s
20 000	0,026s	0,019s	0,020s
10 000	0,014s	0,011s	0,010s

Недостатком алгоритма сортировки слиянием является дополнительный расход памяти для хранения временных массивов-половин. Преимуществом - стабильное время выполнения на любом наборе входных данных.

Быстрая сортировка

Еще одним алгоритмом, в среднем выполняющимся с вычислительной сложностью , являетсябыстрая сортировка. По сравнению с сортировкой слиянием, преимуществом быстрой сортировки является отсутствие необходимости в значительном объеме дополнительной памяти для хранения временных массивов. Быстрая сортировка модифицирует исходный массив непосредственно (in-place).

Суть алгоритма сводится к следующему:

1. Тем или иным образом выбирается некоторый опорный элемент (pivot) в исходном массиве. Например, в качестве опорного элемента может быть случайная позиция, либо серединная позиция.

2. Все элементы, меньшие опорного, располагаются левее, а все элементы большие опорного - правее.

3. Массив условно разбивается на 2 части по опорному элементу, которые сортируются рекурсивно тем же алгоритмом.

4. Как и в сортировке слиянием, по достижению некоторого граничного количества элементов, например N < 10, вместо дальнейшей рекурсии имеет смысл использовать простейший алгоритм сортировки, такой как сортировка выбором.

Продемонстрируем работу данного алгоритма в графической форме, используя тот же самый массив, что и в примере сортировки слиянием. Для упрощения восприятия, не будем применять сортировку выбором при N < 10, а доведем разбиение до минимального количества элементов. В качестве опорного элемента в данном случае будем брать серединную позицию. Итак, для исходного массива из 16 элементов серединной позицией является 8 со значением 12.

Необходимо переупорядочить элементы массива таким образом, чтобы слева от выбранного опорного значения 12 находились все значения, меньшие 12, а правее - большие. Начнем двигаться одновременно слева и справа:

Передвинем индекс слева на ближайшую позицию, в которой находится число, большее или равное опорному. В данном случае, самое первое число уже удовлетворяет данному критерию. Аналогично, найдем позицию для правого индекса с числом, которое меньше опорного элемента. В данном случае, таким числом является 11:

Переставим эти элементы местами:

Продолжим аналогичную процедуру. Следующим ближайшим значением слева, большим или равным опорному, является 17. А ближайшим большим или равным 12, является 5:

Поменяем эти значения местами:

Продолжим процедуру аналогичным образом, пока индексы не пересекутся между собой:

Переставим местами очередную пару:

Продолжим перестановки, и, наконец, достигнем ситуации, в которой индексы пересекутся:

В результате всех приведенных шагов, получены 2 части массива - элементы с индексами от 0 до 4 меньше опорного значения 12, а элементы с индексами от 5 до 15 - больше либо равны 12. Далее процесс следует продолжить рекурсивно на этих частях (при этом массивы нужно разделить лишь логически, копирования не потребуется):

Обработаем аналогично первую часть массива. Серединным элементом является 12:

Потребуются следующие перестановки:

Далее индексы пересекутся, и придется обрабатывать части 11, 5, 8, 0 и 12 отдельно друг от друга. С частью, состоящей из одного элемента 12, делать ничего не нужно. Далее приведено пошаговое выполнение над первой частью из 4 элементов с серединой 8:

Далее массив уже является отсортированным. Итак, возвращаемся на предыдущий уровень, и получим отсортированную часть массива:

Проведем аналогичные действия с оставшейся частью массива:

Далее от массива отколется элемент 14, и сортировка продолжится с серединным элементом 41:

Далее, разделяем массив на две части для рекурсивной обработки:

С правой частью задача сводится к элементарной:

В левой части потребуется большее число шагов:

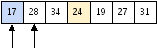
Значение 17 “откалывается”, аналогичная ситуация произойдет со следующим значением 19:

Далее серединным значением является 28:

Дальнейшее разбиение и обработка частей массивов очевидны. В результате будет получен отсортированный фрагмент:

Возвращаясь по рекурсии вверх, логически сформируем итоговый отсортированный массив - физически никаких итоговых действий по слиянию не потребуется:

Оценим вычислительную сложность данного алгоритма. Предположим, что выбор опорного элемента разбивает исходный массив на 2 приблизительно равные части. В таком случае время сортировки определяется временем разбиения + двукратным временем сортировки половин:

Алгоритм разбиения обладает линейной сложностью, т.к. индексы движутся навстречу друг другу и проходят элементы не более 1 раза. Таким образом, получим рекуррентное соотношение, аналогичное оценке алгоритма сортировки слиянием:

Выше уже было доказано, что такое соотношение раскрывается как линейно-логарифмическое:

Как это было наглядно продемонстрировано в примере, предположение о разбиении массива на 2 равные половины является чересчур оптимистичным. В худшем случае, от массива на каждом очередном шаге может “откалываться” лишь одно число, что существенно видоизменит рекуррентное соотношение:

Раскрывая рекурсию, получим следующий ряд:

Из чего, делаем вывод, что в самом худшем случае, вычислительная сложность быстрой сортировки стремится к квадратичной:

На практике, время выполнения быстрой сортировки в среднем случае находится между линейно-логарифмической и квадратичной функцией от N, однако можно подобрать случаи комбинаций входных данных, при которых поведение будет близким к квадратичному. Это делает этот привлекательный алгоритм нестабильным.

Фактически, все определяется выбором качественного опорного элемента, разбивающего массив на максимально равные части. Предсказать такую позицию без сложной обработки невозможно, поэтому рациональной стратегией является выбор позиции случайным образом. Это вносит вероятностную составляющую во время выполнения алгоритма, однако, приводит к неплохим результатам для подавляющего большинства сортируемых наборов данных.

Существуют и другие стратегии выбора опорного элемента - например, подсчет среднего значения, выбор наибольшего из двух первых или последних значений, среднее из трех случайных позиций.

Ниже представлена программная реализация описанного алгоритма, при чем при выборе опорного элемента используется случайная позиция от 0 до N - 1:

void quickSort ( int * _pData, int _N )

{

// На малом количестве элементов используем алгоритм сортировки выбором

if ( _N < 10 )

{

selectionSort( _pData, _N );

return;

}

int leftIndex = -1, rightIndex = _N;

// Случайным образом выбираем опорный элемент

int pivotIndex = rand() % _N;

int pivot = _pData[ pivotIndex ];

// Цикл перераспределения данных вокруг опорного элемента

while ( true )

{

// Двигаем индекс слева до позиции, равной или превышающей опорный элемент

while ( leftIndex < _N && _pData[ ++ leftIndex ] < pivot );

// Двигаем индекс справа в обратном направлении до меньшего опорному значения

while ( rightIndex >= 0 && pivot < _pData[ --rightIndex ] )

if ( rightIndex == leftIndex ) // Прерываемся при пересечении индексов

break;

// Перераспределение завершено

if ( leftIndex >= rightIndex )

break;

// Меняем местами элементы, стоящие не на своих позициях

int temp = _pData[ leftIndex ];

_pData[ leftIndex ] = _pData[ rightIndex ];

_pData[ rightIndex ] = temp;

}

// Особый случай - вытеснение опорного элемента в крайнее положение

if ( leftIndex == 0 )

leftIndex = 1;

else if ( leftIndex == _N )

leftIndex = _N - 1;

// Рекурсивно сортируем две части массива отдельно

quickSort( _pData, leftIndex );

quickSort( _pData + leftIndex, _N - leftIndex );

}

Несмотря на возможную деградацию алгоритма быстрой сортировки до квадратичной вычислительной сложности, именно его используют на практике наиболее часто. В частности, средства сортировки в стандартной библиотеке C (функция qsort) и С++ (алгоритм std::sort) основаны именно на алгоритме быстрой сортировки. В среднем, быстрая сортировка опережает сортировку слиянием, т.к. не использует копирование данных во временные массивы. Ниже представлены эквивалентные замеры производительности, подтверждающие данный вывод:

Размер массива	Случайные данные	Отсортированные данные	Данные в обратном порядке
500 000	0,165s	0,087s	0,098s
200 000	0,063s	0,026s	0,030s
100 000	0,031s	0,012s	0,014s
50 000	0,015s	0,006s	0,007s
20 000	0,006s	0,002s	0,002s
10 000	0,002s	0,001s	0,001s

Сравнение же быстрой сортировки с простейшими методами с квадратичной сложностью для достаточно больших N окончательно убеждает в важности выбора правильного алгоритма. Так для N=100000 элементов, разница между этими двумя алгоритмами для случайного набора данных составляет 23.156 / 0,031 ~= 747 раз!

Сложность базовых операций структур данных

В заключение данной лекции, оценим вычислительную сложность операций ранее рассмотренных базовых структур данных без детальных пояснений.

Операции с векторами характеризуются следующей вычислительной сложностью:

Количество элементов	O(1)
Доступ к i-ой ячейке	O(1)
Вставка в конец	O(1)*
Удаление с конца	O(1)
Вставка в произвольную позицию	O(N)*
Удаление из произвольной позиции	O(N)

Вставка в конец вектора оценивается как амортизированная константная вычислительная сложность. Предсказать ее строго аналитически является нетривиальной задачей. Проблема состоит в том, что вектор может в некоторый момент времени достигнуть размера выделенного блока целиком, вызвав процедуру удвоения с переносом данных в новый блок. До момента роста вычислительная сложность не зависит от размера и является константной O(1). При больших N рост вектора происходит довольно редко, однако в этот редкий момент сложность равна O(N).

Понятие амортизированной сложности можно легко представить на жизненном примере. Предположим, 1 пачка бумаги из 500 листов стоит 40 грн, и бумага продается только целыми пачками. Какова стоимость одного листа бумаги? Наивная логика состоит в делении стоимости пачки на количество листов:

Рассуждая формально, в ситуации, когда бумага закончилась, первый лист бумаги будет стоить 40 грн., поскольку купить меньше целой пачки не представляется возможным. После покупки пачки остальные 499 листов “достанутся” бесплатно. Хотя этот вывод вызывает улыбку у многих людей, это соответствует истине. Конечно, если использовать все 500 листов из купленной пачки, то их средняя стоимость составит 8 коп., исходя из приведенной выше формулы.

Точно также, вставка элемента в конец вектора, вызывающая его рост, будет иметь высокую стоимость, в то время как вставки следующих элементов, не вызывающих рост будут практически мгновенными. Таким образом, амортизированная вычислительная сложность - это среднее арифметическле от сложности обработки достаточно большого количества элементов.

Аналогично, вставка элемента в произвольную позицию вектора, также может привести к его росту, поэтому будем считать ее амортизированной линейной.

Операции со связными списками ведут себя более предсказуемо:

Количество элементов	O(N)
Доступ к i-ой ячейке	O(N)
Вставка в произвольную позицию	O(1)
Удаление из произвольной позиции	O(1)

Связный список заметно привлекательнее при вставке/удалении элементов в произвольной позиции, т.к. это сводится к переназначению связей. В то же время, очевиден проигрыш при определении количества элементов и доступе к i-ой ячейке.

Очереди, реализованные на основе циклического массива фиксированного размера, будут демонстрировать константную вычислительную сложность всех операций. Это очевидно лишь глядя на код реализации, не содержащий ни одного цикла.

Поиск в отображениях и множествах, реализованных на основе массивов или списков характеризуется линейной сложностью. Теоретико-множественные операции (объединение, пересечение, разность) без предварительной сортировки данных в базовых структурах будут обладать квадратичной сложностью, т.к потребуется сравнение каждого элемента с каждым.

Выводы

В данной лекции было введено понятие вычислительной сложности алгоритмов. Была показана ее роль как определяющего фактора, влияющего на быстродействие решения задач. С иллюстративными примерами были перечислены типичные случаи функций, описывающих вычислительную сложность, показаны поверхностные, эмпирические и аналитические способы оценки. Особое внимание было уделено сравнению алгоритмов линейного и бинарного поиска, а также целому семейству классических алгоритмов сортировки. Прочувствовав важность оценки вычислительной сложности, программист должен осознанно подходить к выбору алгоритма для решения задачи.