В результате ее выполнения в динамической памяти формируется структура объектов, в существенной степени напоминающая оригинальный пример из описания понятия деревьев:
Минусом такого способа организации дерева является существенно больший расход оперативной памяти. Каждый узел здесь выделяется динамически отдельно, что приводит к большому количеству операций выделения и освобождения небольшого блока. Общее количество необходимой памяти возрастает, так как каждое выделение имеет собственные накладные служебные расходы, мало зависящие от размера фактически выделенной “полезной” памяти.
Бинарные деревья
Для бинарного дерева, т.е. дерева, в котором имеется не более двух дочерних узлов у каждого узла-родителя, представляется возможным существенно упростить рассмотренные выше структуры данных. В частности, структура дерева с фиксированным количеством узлов упрощается до следующей:
struct Tree
{
struct NodeData
{
TreeNodeLabel m_label;
int m_parentIndex;
int m_leftChildIndex;
int m_rightChildIndex;
};
int m_nNodes;
NodeData * m_pNodes;
};
Используя ограничение на количество дочерних узлов, представляется возможным полностью избавиться от связных списков при хранении данных о дочерних узлах в узле-родителе. Кроме того, удается улучшить вычислительную сложность “проблемных операций” - PARENT и RIGHT_SIBLING - до константной:
int TreeGetParentIndex ( Tree * _pTree, int _nodeIndex )
{
Tree::NodeData * pNodeData = _pTree->m_pNodes + _nodeIndex;
return pNodeData->m_parentIndex;
}
int TreeGetRightSiblingIndex ( Tree * _pTree, int _nodeIndex )
{
Tree::NodeData * pNodeData = _pTree->m_pNodes + _nodeIndex;
Tree::NodeData * pParentNodeData = _pTree->m_pNodes + pNodeData->m_parentIndex;
if ( pParentNodeData->m_leftChildIndex == _nodeIndex )
return pParentNodeData->m_rightChildIndex;
else
return -1;
}
Динамическая структура на основе указателей также может быть упрощена до хранения непосредственной связи с левым и правыми поддеревьями:
struct TreeNode
{
TreeNodelabel m_label;
TreeNode * m_pParent;
TreeNode * m_pLeftChild;
TreeNode * m_pRightChild;
};
Упрощение не влияет на требуемый объем памяти или вычислительную сложность операций, однако заметно упрощает рекурсивную обработку. Например, в процедуре уничтожения дерева удается избавиться от цикла и упростить задачу до элементарных рекурсивных вызовов:
void TreeNodeDestroy( TreeNode * _pNode )
{
if ( _pNode->m_pLeftChild )
NodeDestroy( _pNode->m_pLeftChild );
if ( _pNode->m_pRightChild )
NodeDestroy( _pNode->m_pRightChild );
delete _pNode;
}
Выводы
В данной лекции был рассмотрен абстрактный тип данных “Дерево”, имеющий широкое распространение в программировании при решении различных практических задач. Фактически, деревья могут использоваться для моделирования иерархической структуры любой сложности. Были предложены различные альтернативные структуры данных, реализующие операции с деревьями, с приведением оценок вычислительной сложности.
СТА: Лекция №8 - Бинарные деревья поиска
Версия 2.01, 12 декабря 2014г.
(С) 2012-2014, Зайченко Сергей Александрович, к.т.н, ХНУРЭ, доцент кафедры АПВТ
Характеристическое свойство BST
На основе бинарных деревьев представляется возможным эффективно реализовать АТД “Отображение” и “Множество”, при условии, что ключи могут быть упорядочены по оператору <. Этому условию удовлетворяют большинство используемых на практике типов данных ключей. Для чисел используется естественный смысл операции меньше, для строк - алфавитный порядок, для перечисляемых типов - порядок объявления меток. При необходимости, можно определить смысл операции < для массивов (по аналогии со строками) и структур (исходя из логики понятия).
Предположим, имеется неупорядоченный набор уникальных чисел:
5 2 7 3 9 0 1 4 6 8
Добавляя на каждом шаге числа при последовательном переборе, сформируем из данного набора бинарное дерево с узлами, метками которого являются эти числа, таким образом, что всегда будет соблюдаться следующее характеристическое свойство:
любой ключ, находящийся в левом поддереве, меньше ключа в узле-родителе
любой ключ, находящийся в правом поддереве, больше ключа в узле-родителе.
Если во входном наборе попадется повторяющееся число, его следует либо проигнорировать, либо следует сигнализировать внешней среде об ошибке.
Ниже в графической форме приведена пошаговая процедура добавления рассматриваемой последовательности чисел в дерево. Первое число 5 попадает в корневой узел:
Число 2 меньше числа 5, поэтому оно будет размещено в левом поддереве:
Число 7 больше числа 5, в связи с чем его следует поместить в правом поддереве:
В дальнейшем процедура будет выполняться рекурсивно. Следует сравнивать очередное входное число с текущим узлом-родителем, начиная от корня, и, если вставляемое в дерево новое число-ключ меньше числа в узле-родителе, новый узел должен вставляться в левое поддерево, а если больше - в правое. Число 3 меньше 5, значит следует двигаться по левому поддереву. Число 3 больше 2, соответственно, это число должно стать правым поддеревом для узла с числом 2:
Число 9 больше числа 5 и больше числа 7, его место в правом поддереве узла с числом 7:
Число 0 меньше числа 5 и меньше числа 2, его поместим в левом поддереве узла с числом 2:
Число 1 меньше числа 5, меньше числа 2, однако больше числа 0. Значит, у узла с числом 0 должно появиться правое поддерево:
Число 4 меньше числа 5, больше числа 2 и больше числа 3, соответственно такое число будет размещено в правом поддереве узла с числом 3:
Число 6 больше числа 5, но меньше числа 7. Узел с числом 7 получит левое поддерево:
Число 8 больше 5, больше 7, но меньше 9, следовательно узел 9 получит левое поддерево:
Бинарные деревья, ключи в узлах которых упорядочены в соответствии с продемонстрированным выше характеристическим свойством, называются деревьями бинарного поиска (BST).
Реализация BST
Наиболее удобный способ реализации BST - динамическая структура для деревьев, рассмотренная в предыдущей лекции о деревьях общего назначения. Структура должна сопровождаться типичными операциями АТД “множество” для поиска, вставки и удаления ключей.
bstree.hpp:
#ifndef _BSTREE_HPP_
#define _BSTREE_HPP_
////////////////////////////////////////////////////////////////////////
struct BSTree
{
struct Node
{
int m_key;
Node * m_pParent;
Node * m_pLeft;
Node * m_pRight;
};
Node * m_pRoot;
};
///////////////////////////////////////////////////////////////////////
// Создание объекта-дерева
BSTree * BSTreeCreate ();
// Уничтожение объекта-дерева
void BSTreeDestroy ( BSTree * _pTree );
// Вставка указанного ключа в дерево
void BSTreeInsertKey ( BSTree & _tree, int _key );
// Проверка наличия указанного ключа в дереве
bool BSTreeHasKey ( const BSTree & _tree, int _key );
// Удаление указанного ключа из дерева
void BSTreeDeleteKey ( BSTree & _tree, int _key );
///////////////////////////////////////////////////////////////////////
#endif // _BSTREE_HPP_
Функции создания и уничтожения реализуются аналогично обычным бинарным деревьям:
bstree.cpp
#include "bstree.hpp"
#include <cassert>
// Создание объекта-дерева
BSTree * BSTreeCreate ()
{
BSTree * pTree = new BSTree;
pTree->m_pRoot = nullptr;
return pTree;
}
// Вспомогательная рекурсивная функция для удаления поддерева
void BSTreeDestroy ( BSTree::Node * _pNode )
{
if ( ! _pNode )
return;
BSTreeDestroy( _pNode->m_pLeft );
BSTreeDestroy( _pNode->m_pRight );
delete _pNode;
}
// Уничтожение объекта-дерева
void BSTreeDestroy ( BSTree * _pTree )
{
BSTreeDestroy( _pTree->m_pRoot );
}
Ниже показан пример реализации описанного алгоритма вставки в BST:
// Вспомогательная функция создания нового узла с указанным ключом
BSTree::Node * BSTreeCreateNode ( int _key )
{
// Создаем объект-узел
BSTree::Node * pNewNode = new BSTree::Node;
// Запоминаем в узле значение ключа
pNewNode->m_key = _key;
// Обнуляем все связи узла с соседями
pNewNode->m_pLeft = pNewNode->m_pRight = pNewNode->m_pParent = nullptr;
// Возвращаем созданный узел
return pNewNode;
}
// Вставка указанного ключа в дерево
void BSTreeInsertKey ( BSTree & _tree, int _key )
{
// Особый случай - вставка первого ключа в пустое дерево
BSTree::Node * pCurrent = _tree.m_pRoot;
if ( ! pCurrent )
{
_tree.m_pRoot = BSTreeCreateNode( _key );
return;
}
// Ищем позицию в дереве для вставки нового ключа, начиная с корня
while ( pCurrent )
{
// При равенстве ключей, игнорируем вставку
if ( pCurrent->m_key == _key )
return;
// Когда новый ключ меньше ключа в текущем узле, движемся в левую сторону
else if ( _key < pCurrent->m_key )
{
// Если левое поддерево уже есть, применяем алгоритм к его корню
if ( pCurrent->m_pLeft )
pCurrent = pCurrent->m_pLeft;
// Левого поддерева нет, новый узел становится левым поддеревом
else
{
BSTree::Node * pNewNode = BSTreeCreateNode( _key );
pNewNode->m_pParent = pCurrent;
pCurrent->m_pLeft = pNewNode;
return;
}
}
// Когда новый ключ больше ключа в текущем узле, движемся в правую сторону
else
{
// Если правое поддерево уже есть, применяем алгоритм к его корню
if ( pCurrent->m_pRight )
pCurrent = pCurrent->m_pRight;
else
{
// Правого поддерева нет, новый узел становится правым поддеревом
BSTree::Node * pNewNode = BSTreeCreateNode( _key );
pNewNode->m_pParent = pCurrent;
pCurrent->m_pRight = pNewNode;
return;
}
}
}
}
Теперь, если требуется выяснить имеется ли интересующий ключ в дереве, следует применить подобный рекурсивный алгоритм:
Начать анализ с узла-корня и назначить его текущим.
Сравнить искомый ключ с ключом в текущем узле:
Если искомый ключ меньше ключа в узле, следует рекурсивно выполнить шаг 2 на левом поддереве, либо завершить поиск, если левого поддерева нет.
Если искомый ключ больше ключа в узле, следует рекурсивно выполнить шаг 2 на правом поддереве, либо завершить поиск, если правого поддерева нет.
Если ключи равны, значит искомый узел найден.
Допустим, требуется узнать имеется ли число 4 в дереве. Выполняем описанный выше рекурсивный алгоритм и приходим от корня к искомому узлу. Ниже графически показан процесс обхода бинарного дерева поиска, при помощи цвета заливки выделен пройденный от корня путь:
Ниже приведена реализация данного алгоритма поиска:
// Вспомогательная функция поиска узла с интересующим ключом в дереве
BSTree::Node * BSTreeFindKeyNode ( const BSTree & _tree, int _key )
{
// Начинаем поиск с корневого узла
BSTree::Node * pCurrent = _tree.m_pRoot;
while ( pCurrent )
{
// Если искомый ключ равен ключу из текущего узла, нужный узел найден!
if ( _key == pCurrent->m_key )
return pCurrent;
// Если искомый ключ меньше ключа текущего узла, движемся по левому поддереву
else if ( _key < pCurrent->m_key )
pCurrent = pCurrent->m_pLeft;
// Если искомый ключ больше ключа текущего узла, движемся по правому поддереву
else
pCurrent = pCurrent->m_pRight;
}
// Узел с таким ключом не найден
return nullptr;
}
// Проверка наличия указанного ключа в дереве
bool BSTreeHasKey ( const BSTree & _tree, int _key )
{
// Ключ принадлежит множеству, если имеется узел с таким же ключом
return BSTreeFindKeyNode( _tree, _key ) != nullptr;
}
Фактически, алгоритмы поиска, вставки, удаления по ключу в бинарном дереве поиска во многом похожи. Следует найти либо сам узел в дереве, рекурсивно спускаясь, выбирая направление по результатам сравнения ключей, либо тем же способом найти место его потенциального расположения при вставке.
Вычислительная сложность таких алгоритмов пропорционально зависит от длины пути в дереве, т.е. от высоты дерева. В идеальном случае, когда высота листьев приблизительно одинаковая, количество рассматриваемых в процессе поиска узлов имеет логарифмическую зависимость от общего числа узлов в дереве O(log2 N). Это менее благоприятная вычислительная сложность по сравнению с хэш-таблицами O(1), однако существенно лучшая по сравнению с линейным поиском в массивах или списках O(N).
Симметричный обход BST
Бинарные деревья поиска обладают чрезвычайно полезным свойством при симметричном обходе. Напомним, при симметричном обходе сначала рекурсивно посещается левое поддерево, затем узел-родитель, затем правое поддерево. Характеристическое свойство, использованное при построении дерева, при таком способе обхода обеспечивает упорядоченность ключей по возрастанию:
0 1 2 3 4 5 6 7 8 9
Это свойство бинарных деревьев поиска может быть использовано как один из способов сортировки данных. Чтобы вывести какие-либо данные в отсортированном порядке, достаточно построить из них дерево бинарного поиска, а затем обойти симметрично, формируя последовательность-результат.
Ниже приведено объявление и реализация симметричного обхода BST:
bstree.hpp:
// ...
typedef void ( * BSTreeWalkFunction ) ( const BSTree::Node & _node );
void BSTreeSymmetricWalk ( const BSTree & _tree, BSTreeWalkFunction _f );
// ...
bstree.cpp:
// …
// Вспомогательная функция симметричного обхода поддерева
void BSTreeSymmetricWalk ( const BSTree::Node * _pNode, BSTreeWalkFunction _f )
{
// Проверка на пустую ветку
if ( ! _pNode )
return;
// Обход левого поддерева
BSTreeSymmetricWalk( _pNode->m_pLeft, _f );
// Посещение текущего родительского узла
( * _f )( * _pNode );
// Обход правого поддерева
BSTreeSymmetricWalk( _pNode->m_pRight, _f );
}
// Симметричный обход дерева
void BSTreeSymmetricWalk ( const BSTree & _tree, BSTreeWalkFunction _f )
{
BSTreeSymmetricWalk( _tree.m_pRoot, _f );
}
Учитывая такое свойство, реализация поиска минимального и максимального ключа в дереве становится тривиальной - достаточно найти самый левый и самый правый узел в дереве соответственно:
// Поиск узла с минимальным ключом - на каждом шаге движемся по левому поддереву:
BSTree::Node * BSTreeMinimumNode ( BSTree::Node * _pNode )
{
assert( _pNode );
BSTree::Node * pCurrent = _pNode;
while ( pCurrent && pCurrent->m_pLeft )
pCurrent = pCurrent->m_pLeft;
return pCurrent;
}
// Поиск минимального ключа - извлекаем из узла с минимальным ключом
int BSTreeMinimum ( const BSTree & _tree )
{
BSTree::Node * pMinimumNode = BSTreeMinimumNode( _tree.m_pRoot );
return pMinimumNode->m_key;
}
// Поиск узла с максимальным ключом - на каждом шаге движемся по правому поддереву:
BSTree::Node * BSTreeMaximumNode ( BSTree::Node * _pNode )
{
assert( _pNode );
BSTree::Node * pCurrent = _pNode;
while ( pCurrent && pCurrent->m_pRight )
pCurrent = pCurrent->m_pRight;
return pCurrent;
}
// Поиск максимального ключа - извлекаем из узла с максимальным ключом
int BSTreeMaximum ( const BSTree & _tree )
{
BSTree::Node * pMaximumNode = BSTreeMaximumNode ( _tree.m_pRoot );
return pMaximumNode >m_key;
}
Удаление узлов из BST
Для реализации удаления первым шагом является поиск узла. Однако, при удалении узла мы также обязаны сохранить выполнение характеристического свойства, какова бы ни была структура дерева и местоположение удаляемого узла.
Случаи, когда удаляется листовой узел, тривиальны. Удаляемый узел просто отцепляется от родителя. Например, удаление узла 8 не вызывает никаких сложностей:
Если удаляется узел-родитель, имеющий только одно из поддеревьев, то корень поддерева становится на место узла-родителя. Удалим узел с ключом 3:
Если же удаляется узел-родитель, имеющий оба поддерева, следует на его место поставить узел с минимальным ключом из правого поддерева. Фактически, необходимо найти узел, являющийся следующим относительно удаляемого при симметричном обходе. Допустим удаляется корневой узел 5, на его место становится узел 6, являющийся минимальным в правом поддереве 9. Особую аккуратность при переназначении связей в деревьях следует проявить, если следующим узлом является непосредственный правый дочерний узел удаляемого узла.
Следует отметить, что алгоритм принципиально не изменится, если вместо следующего узла (минимального узла из правого поддерева) будет использоваться предыдущий (максимальный узел из левого поддерева), поскольку такая замена является симметричной.
Ниже приведена реализация описанного алгоритма удаления узла:
// Вспомогательная функция пересадки узла:
// заменяет все ссылки на указанный узел на ссылки на другой узел (либо на nullptr)
void BSTreeTransplant ( BSTree & _tree, BSTree::Node * _pNode, BSTree::Node * _pOtherNode )
{
// Если у пересаживаемого узла нет родителя, значит он является корневым
if ( ! _pNode->m_pParent )
{
// Подменяем корневой узел
assert( _pNode == _tree.m_pRoot );
_tree.m_pRoot = _pOtherNode;
}
// Пересаживаемый узел является левым дочерним у своего родителя?
else if ( _pNode->m_pParent->m_pLeft == _pNode )
// Левым дочерним узлом родителя будет другой узел
_pNode->m_pParent->m_pLeft = _pOtherNode;
// Пересаживаемый узел является правым дочерним у своего родителя?
else if ( _pNode->m_pParent->m_pRight == _pNode )
// Правым дочерним узлом родителя будет другой узел
_pNode->m_pParent->m_pRight = _pOtherNode;
// Других случаев быть не может!
else
assert( 0 );
// Новым родителем пересаженного узла является родитель прежнего узла
if ( _pOtherNode )
_pOtherNode->m_pParent = _pNode->m_pParent;
}
// Удаление указанного ключа из дерева
void BSTreeDeleteKey ( BSTree & _tree, int _key )
{
// Обнаруживаем узел с интересующим ключом
BSTree::Node * pNode = BSTreeFindKeyNode( _tree, _key );
if ( ! pNode )
// Узел не найден, игнорируем запрос (либо сообщаем об ошибке)
return;
// Если у удаляемого узла нет левого поддерева, подменяем его правым поддеревом.
// Даже если правого поддерева нет, пересадка корректно переназначит связи.
if ( ! pNode->m_pLeft )
BSTreeTransplant( _tree, pNode, pNode->m_pRight );
// Если у удаляемого узла нет правого поддерева, подменяем его левым поддеревом.
else if ( ! pNode->m_pRight )
BSTreeTransplant( _tree, pNode, pNode->m_pLeft );
// Самый сложный случай - удаляемый узел имеет и левое, и правое поддерево
else
{
// Ищем минимальный узел в правом поддереве удаляемого узла
BSTree::Node * pNextNode = BSTreeMinimumNode( pNode->m_pRight );
// Если родителем найденного узла не является сам удаляемый узел,
// необходимо отделить его от текущего узла-родителя. if ( pNextNode->m_pParent != pNode )
{
// У него точно нет левого поддерева, иначе бы он не был минимальным.
// Подменяем его правым поддеревом (возможно пустым).
BSTreeTransplant( _tree, pNextNode, pNextNode->m_pRight );
// Сцепляем выбранный узел с правым поддеревом удаляемого узла
pNextNode->m_pRight = pNode->m_pRight;
pNextNode->m_pRight->m_pParent = pNextNode;
}
// Сцепляем выбранный узел с родительским узлом удаляемого узла
BSTreeTransplant( _tree, pNode, pNextNode );
// Сцепляем выбранный узел с левым поддеревом удаляемого узла
pNextNode->m_pLeft = pNode->m_pLeft;
pNextNode->m_pLeft->m_pParent = pNextNode;
}
// Удаляем указанный объект-узел
delete pNode;
}
Тестовая программа
Проверим работу реализованного BST при помощи несложной тестовой программы:
#include "bstree.hpp"
#include <cassert>
#include <iostream>
// Функция обратного вызова для симметричного обхода: печатает ключ в узле
void printNode ( const BSTree::Node & _node )
{
std::cout << _node.m_key << ' ';
}
int main ()
{
// Создаем объект-BST
BSTree * pTree = BSTreeCreate();
// Определяем последовательность ключей для вставки
int keys[] = { 5, 2, 7, 3, 9, 0, 1, 4, 6, 8 };
int nKeys = sizeof( keys ) / sizeof( int );
// Вставляем ключи в BST в определенном выше порядке
for ( int i = 0; i < nKeys; i++ )
BSTreeInsertKey( * pTree, keys[ i ] );
// Каждый из вставленных ключей точно находится в дереве
for ( int i = 0; i < nKeys; i++ )
assert( BSTreeHasKey( * pTree, keys[ i ] ) );
// Сопоставляем минимальный и максимальный ключи с ожидаемыми
assert( BSTreeMinimum( * pTree ) == 0 );
assert( BSTreeMaximum( * pTree ) == 9 );
// Выполняем симметричных обход с распечаткой ключей на консоли
BSTreeSymmetricWalk( * pTree, & printNode );
std::cout << std::endl;
// Тестируем удаление ключей
for ( int i = 0; i < nKeys; i++ )
{
// Удаляем очередной ключ
BSTreeDeleteKey( * pTree, keys[ i ] );
// После удаления ключ не должен быть представлен во множестве
assert( ! BSTreeHasKey( * pTree, keys[ i ] ) );
// Другие, еще не удаленные ключи, должны остаться во множестве
for ( int k = i + 1; k < nKeys; k++ )
assert( BSTreeHasKey( * pTree, keys[ k ] ) );
}
// Уничтожаем объект-BST
BSTreeDestroy( pTree );
}
При вызове данной программы, убеждаемся в упорядоченности вывода ключей при обходе:
Несбалансированные BST и вращение
Бинарное дерево поиска, у которого для любого узла-родителя количество дочерних узлов в левом и правом поддереве приблизительно равны, называется сбалансированным. Обратный случай, когда имеется существенный перевес у одного из двух поддеревьев, образует несбалансированное дерево. Вычислительная сложность процедуры поиска имеет логарифмическую сложность лишь для сбалансированных деревьев. Если баланс поддеревьев нарушен, сложность процедуры поиска в худшем случае вырождается до линейной.
Худшим случаем для работы BST является ввод уже упорядоченной последовательности, например:
0 1 2 3 4 5 6 7 8 9
Описанный выше алгоритм вставки для такой последовательности сформирует крайне неудачное с точки зрения поиска бинарное дерево - абсолютно несбалансированное BST, несмотря на соблюдение характеристического свойства:
Фактически, такое дерево превращается в односвязный список с линейной вычислительной сложностью поиска. Очевидно, в базовой форме деревья бинарного поиска не могут успешно обрабатывать уже упорядоченные последовательности.
Существует ряд алгоритмов автоматической балансировки деревьев, дополняющих базовую идею BST. Большинство из них основано на применении операции вращения. Суть вращения состоит в повороте одной из связей (оси вращения) в дереве по часовой (правое вращение) или против часовой стрелки (левое вращение) в зависимости от текущей потребности алгоритма. Вращение в конкретной области дерева помогает уменьшить возможный дисбаланс между высотами левого и правого поддеревьев. В какой именно момент времени и какую связь следует повернуть зависит от используемого алгоритма. Ниже рассмотрены сами операции вращения.
Предположим имеется следующее дерево, и тот или иной алгоритм принимает решение осуществить правое вращение связи между узлами-полюсами B и D. Выбранные узлы можно поменять местами, при условии, что характеристическое свойство BST не будет нарушено:
В начале узлы-полюса B и D вокруг оси вращения следует расцепить:
Затем, правое поддерево C левого полюса B следует перекрепить к освободившемуся месту в левом поддереве правого полюса D:
Затем можно перекрепить левый полюс B с родительским узлом правого полюса D, поскольку после расцепления полюсов эта связь является свободной. В частном случае, родительской связи может не быть, в таком случае D является корневым узлом дерева, а новым корнем станет B:
Наконец, можно прикрепить правый полюс D к левому полюсу B со свободной правой стороны, тем самым завершая операцию вращения без нарушения характеристического свойства BST:
Любого из соседних узлов - A, C, E, а также родительской связи в дереве может не быть, что не изменит сути рассмотренного алгоритма, лишь упростив его шаги.
Левое вращение реализуется аналогично и симметрично, фактически, следует выполнить шаги алгоритма правого вращения в обратном порядке.
Следует отметить, что операция вращения является локальной относительно выбранной оси. Модифицируются лишь связи узлов-полюсов B и D, а также родительская связь узла-поддерева C, ключ которого находится между ключами во вращаемых узлах-полюсах. Состояние других узлов не модифицируется, а значит данная операция обладает высоким быстродействием.
Ниже приведен код функций, реализующий левое и правое вращение:
void BSTreeLeftRotate ( BSTree & _tree, BSTree::Node * _l )
{
// l - левый полюс вращения, r - правый полюс вращения.
// Ось вращения - связь между l и r
BSTree::Node* r = _l->m_pRight;
// Если правого полюса нет, вращать нечем
if ( ! r )
return;
// Перекрепляем промежуточный узел к правой ветви левого полюса
_l->m_pRight = r->m_pLeft;
if ( _l->m_pRight )
_l->m_pRight->m_pParent = _l;
// Перекрепляем родительскую связь с левого полюса на правый
// Случай 1: левый полюс - корень, правый полюс становится новым корнем
// Случай 2: левый полюс является левым ребенком своего родителя
// Случай 3: левый полюс является правым ребенком своего родителя
r->m_pParent = _l->m_pParent;
if ( ! r->m_pParent )
_tree.m_pRoot = r;
else if ( _l == _l->m_pParent->m_pLeft )
_l->m_pParent->m_pLeft = r;
else if ( _l == _l->m_pParent->m_pRight )
_l->m_pParent->m_pRight = r;
else
// Иная ситуация невозможна
assert( 0 );
// Воссоздаем ось между полюсами в противоположном направлении
r->m_pLeft = _l;
_l->m_pParent = r;
}
void BSTreeRightRotate ( BSTree & _tree, BSTree::Node * _r )
{
// l - левый полюс вращения, r - правый полюс вращения.
// Ось вращения - связь между l и r
BSTree::Node* l = _r->m_pLeft;
// Если левого полюса нет, вращать нечем
if ( ! l )
return;
// Перекрепляем промежуточный узел к левой ветви правого полюса
_r->m_pLeft = l->m_pRight;
if ( _r->m_pLeft )
_r->m_pLeft->m_pParent = _r;
// Перекрепляем родительскую связь с правого полюса на левый
// Случай 1: правый полюс - корень, левый полюс становится новым корнем
// Случай 2: правый полюс является левым ребенком своего родителя
// Случай 3: правый полюс является правым ребенком своего родителя
l->m_pParent = _r->m_pParent;
if ( ! l->m_pParent )
_tree.m_pRoot = l;
else if ( _r == _r->m_pParent->m_pLeft )
_r->m_pParent->m_pLeft = l;
else if ( _r == _r->m_pParent->m_pRight )
_r->m_pParent->m_pRight = l;
else
// Иная ситуация невозможна
assert( 0 );
// Воссоздаем ось между полюсами в противоположном направлении
l->m_pRight = _r;
_r->m_pParent = l;
}
Красно-черные деревья
Одним из наиболее популярных алгоритмов автоматической балансировки BST является алгоритм красно-черных деревьев. Обычно именно этот алгоритм используется при реализации стандартных библиотечных средств для отображений и множеств на основе BST.
Идея данного алгоритма состоит в расширении объекта-узла еще одной переменной, обозначающей цвет узла: красный или черный. Выбор таких названий является условным, смысл состоит в разделении всех узлов на 2 типа:
struct RBTree
{
struct Node
{
int m_key;
enum Color { RED, BLACK } m_color;
Node * m_pParent;
Node * m_pLeft;
Node * m_pRight;
};
Node * m_pRoot;
};
В любом состоянии красно-черное дерево должно сохранять следующие свойства, помимо характеристического свойства BST:
Корень дерева является черным узлом.
Если узел красный, его дочерние узлы могут быть только черными.
Для каждого промежуточного узла все пути от него до его листьев содержат одинаковое количество черных узлов.
Исходя из условий 2 и 3, можно сделать вывод, что при соблюдении всех условий, высота левого и правого поддерева в самом худшем случае отличается не более чем в 2 раза (за счет возможных дополнительных красных промежуточных узлов между черными узлами). Из этой структурной особенности вытекает, что операции вставки, поиска и удаления будут характеризоваться логарифмической вычислительной сложностью, а самои дерево будет приближенно сбалансированным.
Реализация функций создания и уничтожения дерева, поиска интересующего ключа, минимального и максимального ключей, вращения узлов, обхода - ни чем не отличается от рассмотренной выше базовой реализации бинарных деревьев поиска. Принципиально отличаются только операции вставки и удаления узлов, поскольку должны сохраняться дополнительные, по сравнению с BST, свойства.
Подробно рассмотрим алгоритм вставки. Каждый новый вставляемый узел должен быть изначально назначен красным. В начале выполняются обычные действия по вставке ключа в BST, как и в базовой реализации, а затем запускается дополнительная процедура, обеспечивающая сохранение специальных свойств красно-черных деревьев. Собственно, после вставки необходимо выявлять возможные проблемы двух типов:
корень красного цвета;
красный дочерний узел прикреплен к красному узлу-родителю.
Первая проблема решается путем перекраски корневого узла в черный цвет. Вторая проблема сложнее, и следует рассмотреть несколько случаев ее решения:
Новый красный узел A прикрепляется к родительскому красному узлу B слева, а также имеется узел-”дядя” D, который также является красным. Следует перекрасить узлы B и D в черный цвет, а узел-”дед” C - наоборот в красный:
Новый красный узел B прикрепляется к родительскому красному узлу A справа, а также имеется узел-”дядя” D, который также является красным. Аналогично, следует перекрасить узлы A и D в черный цвет, а узел-”дед” C - в красный:
Новый красный узел A прикрепляется к родительскому красному узлу B слева, а узла-”дяди” D в дереве либо нет, либо он является черным. Следует осуществить вращение по оси между узлами B и C, поменяв их цветами:
Новый красный узел B прикрепляется к родительскому красному узлу A справа, , а узла-”дяди” D в дереве нет, либо он является черным. Следует осуществить вращение по оси между узлами A и B, а затем свести задачу к предыдущему случаю:
Возможны также зеркально симметричные случаи, которые разрешаются аналогично.
В результате применения правил коррекции №1 и №2 на основе вращений, нарушение свойств красно-черного дерева может повториться для узлов, находящихся выше по иерархии, т.к. в результате получается поддерево с красным корнем. В таком случае все корректирующие операции алгоритма следует повторно применить на следующем уровне и так далее, пока дерево в итоге не стабилизируется.
Ниже представлен программный код, реализующий описанный алгоритм вставки с коррекциями:
// Функция создания нового элемента красно-черного дерева
RBTree::Node * RBTreeCreateNode ( int _key )
{
RBTree::Node * pNewNode = new RBTree::Node;
pNewNode->m_key = _key;
// Важно! По умолчанию новый узел всегда красный!
pNewNode->m_color = RBTree::Node::RED;
pNewNode->m_pLeft = pNewNode->m_pRight = pNewNode->m_pParent = nullptr;
return pNewNode;
}
// Базовая функция вставки, аналогично классической вставке в BST.
// Дополнительно возвращает указатель на новый узел
RBTree::Node * RBTreeInsertBase ( RBTree & _tree, int _key )
{
// Особый случай - вставка первого ключа в пустое дерево
RBTree::Node * pCurrent = _tree.m_pRoot;
if ( ! pCurrent )
{
_tree.m_pRoot = RBTreeCreateNode( _key );
return _tree.m_pRoot;
}
// Ищем позицию в дереве для вставки нового ключа, начиная с корня
while ( pCurrent )
{
// При равенстве ключей, игнорируем вставку
if ( pCurrent->m_key == _key )
return nullptr;
// Когда новый ключ меньше ключа в текущем узле, движемся в левую сторону
else if ( _key < pCurrent->m_key )
{
// Если левое поддерево уже есть, применяем алгоритм к его корню
if ( pCurrent->m_pLeft )
pCurrent = pCurrent->m_pLeft;
// Левого поддерева нет, новый узел становится левым поддеревом
else
{
RBTree::Node * pNewNode = RBTreeCreateNode( _key );
pNewNode->m_pParent = pCurrent;
pCurrent->m_pLeft = pNewNode;
return pNewNode;
}
}
// Когда новый ключ больше ключа в текущем узле, движемся в правую сторону
else
{
// Если правое поддерево уже есть, применяем алгоритм к его корню
if ( pCurrent->m_pRight )
pCurrent = pCurrent->m_pRight;
// Правого поддерева нет, новый узел становится правым поддеревом
else
{
RBTree::Node * pNewNode = RBTreeCreateNode( _key );
pNewNode->m_pParent = pCurrent;
pCurrent->m_pRight = pNewNode;
return pNewNode;
}
}
}
// Дойти до данного кода при корректной реализации невозможно!
assert( 0 );
return nullptr;
}
// Функция извлечения цвета узла. Если узла нет - представим, что он черный
RBTree::Node::Color RBTreeColorOf ( const RBTree::Node * _pNode )
{
return ( _pNode ) ? _pNode->m_color : RBTree::Node::BLACK;
}
// Основная процедура вставки нового ключа в красно-черное дерево
void RBTreeInsertKey ( RBTree & _tree, int _key )
{
// Вызываем базовую процедуру вставки ключа в BST
RBTree::Node * x = RBTreeInsertBase( _tree, _key );
// Если узел не был вставлен, корректировать нечего
if ( ! x )
return;
// Пытаемся обнаружить пару родитель-дочерний узел красного цвета
RBTree::Node * p;
while ( x && ( p = x->m_pParent ) && RBTreeColorOf( p ) == RBTree::Node::RED )
{
// Для коррекций иерархии необходим узел-дед
RBTree::Node* pp = p->m_pParent;
// Является ли узел-родитель левым ребенком узла-деда?
if ( p == pp->m_pLeft )
{
// Имеется ли красный узел-дядя? (случаи 1 и 2)
RBTree::Node* y = pp->m_pRight;
if ( RBTreeColorOf( y ) == RBTree::Node::RED )
{
// Делаем родителя и дядю черными, а дедушку - красным
p->m_color = RBTree::Node::BLACK;
y->m_color = RBTree::Node::BLACK;
pp->m_color = RBTree::Node::RED;
// Продолжаем анализ с уровня дедушки
x = pp;
}
else
{
// Является ли новый узел правым поддеревом родителя? (случай 4)
if ( x == p->m_pRight )
{
// Делаем левое вращение, сводим к случаю 3
x = p;
RBTreeLeftRotate( _tree, x );
}
p = x->m_pParent;
pp = p->m_pParent;
// Случай 3 - делаем родителя черным, дедушку красным,
// затем вращаем ось между родителем и дедушкой вправо
p->m_color = RBTree::Node::BLACK;
if ( pp )
{
pp->m_color = RBTree::Node::RED;
RBTreeRightRotate( _tree, pp );
}
}
}
// Узел-родитель является правым ребенком узла-деда
else
{
// Имеется ли красный узел-дядя? (случаи 1 и 2)
RBTree::Node* y = pp->m_pLeft;
if ( RBTreeColorOf( y ) == RBTree::Node::RED )
{
// Делаем родителя и дядю черными, а дедушку - красным
p->m_color = RBTree::Node::BLACK;
y->m_color = RBTree::Node::BLACK;
pp->m_color = RBTree::Node::RED;
// Продолжаем анализ с уровня дедушки
x = pp;
}
else
{
// Является ли новый узел левым поддеревом родителя? (случай 4)
if ( x == p->m_pLeft )
{
// Делаем правое вращение, сводим к случаю 3
x = p;
RBTreeRightRotate( _tree, x );
}
p = x->m_pParent;
pp = p->m_pParent;
// Случай 3 - делаем родителя черным, дедушку красным,
// затем вращаем ось между родителем и дедушкой влево
p->m_color = RBTree::Node::BLACK;
if ( pp )
{
pp->m_color = RBTree::Node::RED;
RBTreeLeftRotate( _tree, pp );
}
}
}-
}
// Решаем проблему со цветом корневого узла
_tree.m_pRoot->m_color = RBTree::Node::BLACK;
}
Попробуем применить описанный и реализованный алгоритм к отсортированной по возрастанию последовательности от 0 до 9, которая “повергла в уныние” классический вариант бинарного дерева поиска. В начале вставляется первый ключ 0, который становится черным корнем:
Узел 1 прикрепляется справа базовым алгоритмом, и дерево при этом не нуждается в коррекциях:
Узел 2 прикрепляется базовым алгоритмом справа, при этом нарушая правило красно-черного дерева о черных дочерних узлах красного родительского узла. Это случай 3 из рассмотренных коррекций, поскольку узла-дяди в дереве нет, а вращать узлы 1 и 2 между собой не требуется. На первом шаге меняем цвета узлов 0 (дед) и узлов 1 (родитель), а затем осуществляем левое вращение по оси между 0 и 1:
Узел 3 также формирует пару красных узлов родитель-потомок, однако эта ситуация относится к случаю 1 из описанных коррекций, поскольку узел 0 в данный момент является красным узлом-дядей по отношению к 3. Соответственно, следует перекрасить деда, дядю и родителя в противоположные цвета. В конце, цвет деда обращается в черный еще раз, как корня дерева:
Узел 4 повторяет ситуацию с узлом 2 (коррекция №3), на этом дерево стабилизируется:
Обработка вставки узла 5 похожа на обработку вставки узла 3:
Обработка вставки узла 6 похожа на обработку вставки узлов 2 и 4. В результате применения коррекции №3, получаем стабильное дерево:
Вставка узла 7 активизирует большее число преобразований в дереве. В начале применяется коррекция №1, т.к. имеется узел-дядя 4 красного цвета. Это образует проблему с красными узлами 3 и 5. Новый случай активизирует коррекцию №3 при узле-деде 1, который является корневым в данный момент. Это преобразование приводит к получению нового корня 3:
Вставка узла 8 - прямое соответствие коррекции №3, без дальнейших распространений:
Наконец вставка числа 9 - это последовательное применение коррекции №1, затем №3, а затем перекрашивание корня в черный цвет:
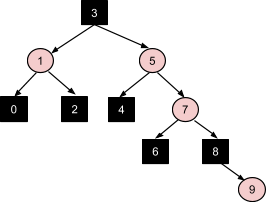
В результате получаем красно-черное дерево, у которого высота любого поддерева не превышает высоту братского поддерева более чем в 2 раза, что позволяет сохранить логарифмическую вычислительную сложность всех операций.
Реализация удаления узлов из красно-черного дерева является еще более громоздкой чем вставка. Основная идея аналогична - в результате выполнения базового алгоритма удаления узла из BST может быть нарушено одно из свойств красно-черного дерева, которое следует незамедлительно восстановить при помощи перекрашиваний и вращений. Более подробно об этом алгоритме можно прочесть в литературе, например, в книге Т. Кормена в главе №13 “Красно-черные деревья”, пункт 13.4 “Удаление”.
Выводы
В данной лекции был рассмотрен популярный алгоритм бинарных деревьев поиска (BST), имеющий широкое практическое применение благодаря логарифмической вычислительной сложности. Свойство упорядоченности ключей при симметричном обходе BST может быть использовано как один из возможных способов сортировки набора ключей. BST в худшем случае может выродиться до односвязного списка с линейной сложностью поиска, при условии вставки уже упорядоченных узлов. Улучшить поведение BST в такой ситуации могут алгоритмы, создающие сбалансированные деревья, например, красно-черные деревья.
СТА: Лабораторная работа №1 - Динамические структуры данных и АТД
Версия 2.0, 22 сентября 2013г.
(С) 2012-2013, Зайченко Сергей Александрович, к.т.н, ХНУРЭ, доцент кафедры АПВТ
Правила выполнения лабораторной работы
Лабораторная работа выполняется либо бригадой из 2 человек, либо индивидуально. Если студент претендует на оценку “отлично”, работа должна выполняться полностью индивидуально.
В работе на выбор студента предлагаются варианты трех уровней сложности:
Базовый уровень - оценка в интервале 15-20 баллов.
Углубленный уровень - оценка в интервале 21-25 баллов.
Амбициозный уровень - оценка не менее 25 баллов + бонусные баллы на усмотрение преподавателя.
Реализовывать задачи необходимо исключительно на языке программирования С++.
Работа оценивается не только по корректности функционирования решений задач, но и по культуре оформления исходного кода в читабельном виде, адекватности разбиения решения на модули и функции.
Поскольку одной из основных целей данного курса является изучение способов построения классических структур данных, при реализации задач запрещается использовать готовые библиотечные реализации этих структур.
Защита работы:
устная и короткая без отчета в случае защиты в день лабораторной работы;
с полноценным печатным отчетом и ответами на теоретические вопросы в случае защиты в другие дни.
Неприемлемым нарушением считается копирование исходного кода программ у другой бригады или из любых других источников тем или иным способом. В случае подозрения на плагиат, преподаватель оставляет за собой право не засчитывать решение полностью или частично, в зависимости от уровня понимания бригадой написанного кода. Уровень понимания может устанавливаться дополнительными вопросами к каждому из участников бригады по коду конкретной программы, по использованным в ней конструкциям языка программирования. В качестве проверки на понимание могут быть запрошены некоторые изменения поведения программы, отклоняющиеся от оригинальных условий задачи.
Пропуск лабораторной работы, независимо от уважительности причин, не освобождает от сдачи работы. В случае пропуска следует самостоятельно найти методические указания у сокурсников или преподавателя, согласовать с преподавателем вариант задания, в домашних условиях либо с другой группой выполнить лабораторную работу, подготовить отчет и пройти защиту.
Литература к лабораторной работе
Р. Седжвик “Алгоритмы на С++”: