
- •Пояснювальна записка
- •1 Общая характеристика, особености и архитектурные принципы организации ngn
- •2 Анлиз базовых моделей технологий сетевого управления
- •3 Анализ технологий и протоколов систем сигнализации ngn
- •4 Анализ взаимодействия технологии управления и систем сигнализации на основе softswitch
- •5 Типовая методика расчета доставки управляющий и сигнальной информации
- •6 Охрана труда
5 Типовая методика расчета доставки управляющий и сигнальной информации
Проанализируем характеристики доставки управляющей и сигнальной информации пакетной (IP/ATM) сети ядра, использующей технологию синхронной цифровой иерархии (Synchronous Digital Hierarchy, SDH) [8, 19] и имеющей ориентированную кольцевую топологию, изображенную на рис. 5.1.

Рисунок 5.1 – Ориентированная кольцевая топология
информационной сети связи
Все
сетевые пункты в ней обмениваются
информацией между собой с помощью
сигнальных сообщений, которые передаются
по кольцу попакетно в одном направлении
и все пакеты (ячейки ATM)
имеют одинаковую длину 53 байта. По кольцу
совершает поступательное движение
синхронный транспортный модуль технологии
SDH вместимостью
 (
( )
пакетов. Проходя мимо сетевого пункта,
он освобождается от данных, дошедших
по назначению, и перезагружается так,
что из совокупности пакетов, прибывших
с STM и адресованных дальше, а также
находившихся в этом сетевом пункте на
ожидании, дальше отправляются наиболее
важные, но не более
)
пакетов. Проходя мимо сетевого пункта,
он освобождается от данных, дошедших
по назначению, и перезагружается так,
что из совокупности пакетов, прибывших
с STM и адресованных дальше, а также
находившихся в этом сетевом пункте на
ожидании, дальше отправляются наиболее
важные, но не более штук. Число мест для ожидания пакетов
на всех пунктах будем считать
неограниченным. Фактически за время
своей доставки пакет может быть несколько
раз задержан на промежуточных пунктах.
штук. Число мест для ожидания пакетов
на всех пунктах будем считать
неограниченным. Фактически за время
своей доставки пакет может быть несколько
раз задержан на промежуточных пунктах.
 ,
(5.1)
,
(5.1)
где
 — число пакетов из потока от пункта
— число пакетов из потока от пункта к пункту
к пункту ,
возникающих на
,
возникающих на в промежутке между
в промежутке между -м
и (
-м
и (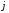 +1)-м
прохождениемSTM
мимо нее. Предположим, что процессы
+1)-м
прохождениемSTM
мимо нее. Предположим, что процессы
 независимы в совокупности и стационарны,
с произвольными производящими функциями
и конечными моментами трех порядков,
для любой пары
независимы в совокупности и стационарны,
с произвольными производящими функциями
и конечными моментами трех порядков,
для любой пары случайные величины
случайные величины при
при независимы и одинаково распределены:
независимы и одинаково распределены:
 ,
(5.2)
,
(5.2)
 ,
(5.3)
,
(5.3)
 .
(5.4)
.
(5.4)
Предположим наличие следующих приоритетов:
– пакеты одного потока всегда обслуживаются в порядке поступления;
– каждый пункт в первую очередь отправляет с STM те пакеты, которые адресованы дальше по кольцу;
– между
потоками сообщений, адресованными к
одному пункту (например, к
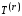 ),
приоритеты могут быть распределены
произвольно и задаются подстановкой
),
приоритеты могут быть распределены
произвольно и задаются подстановкой
 ,
,
где
 - приоритет потока от пункта
- приоритет потока от пункта к пункту
к пункту .
.
При анализе характеристик доставки управляющей и сигнальной информации основе предложенной модели используем следующие обозначения:
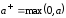 ;
;
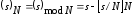 ;
;
 -
число пакетов из потока
-
число пакетов из потока
 ,
находящихся на всех пунктах сети перед
их (
,
находящихся на всех пунктах сети перед
их ( +1)-м
доступом в сеть;
+1)-м
доступом в сеть;
если
случайные величины
 сходятся по распределению при
сходятся по распределению при ,
то предел обозначается той же буквой:
,
то предел обозначается той же буквой:
 .
.
Ниже встречаются также уравнения вида

 ,
(5.5)
,
(5.5)
где
 ;
;
 -
целочисленная случайная величина,
причем
-
целочисленная случайная величина,
причем
 ,
, .
Это уравнение при любом
.
Это уравнение при любом (
( )
имеет ровно
)
имеет ровно комплексных корней
комплексных корней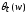 ,
, таких, что
таких, что .
Обозначая
.
Обозначая ,
будем всегда нумеровать корни так, что
,
будем всегда нумеровать корни так, что .
.
Время
оборота STM
по кольцу будем считать равным единице,
а промежуток между
 -м
и (
-м
и ( )-м
его прохождением мимо сетевого пункта
назовем
)-м
его прохождением мимо сетевого пункта
назовем -м
сеансом.
-м
сеансом.
При расчете характеристик доставки информации будем предполагать, что для кольцевой сети выполняется условие эргодичности
 ,
,
 (5.6)
(5.6)
и
системы находятся в стационарном режиме.
Номера оборотов STM
будем считать по прохождению его мимо
пункта
 .
.
Пакеты
из потока
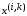 возникают с интенсивностью
возникают с интенсивностью .
Таким образом, если найти распределение
.
Таким образом, если найти распределение — количества всех находящихся в сети
пакетов от пункта
— количества всех находящихся в сети
пакетов от пункта к пункту
к пункту ,
то из формулы Литтла получим доставки
пакета.
,
то из формулы Литтла получим доставки
пакета.
 .
(5.7)
.
(5.7)
Обозначим через
 (5.8)
(5.8)
число
пакетов, требующих транзита через
 и находящихся на всех пунктах сети перед
их (
и находящихся на всех пунктах сети перед
их ( )-м
доступом, а через
)-м
доступом, а через
 (5.9)
(5.9)
-
число таких пакетов, возникающих на
всех станциях сети между их
 -м
и (
-м
и ( )-м
доступом.
)-м
доступом.
Из
определения поступающих потоков следует,
что
 — независимы и одинаково распределены
при
— независимы и одинаково распределены
при с производящей функцией
с производящей функцией
 (5.10)
(5.10)
и конечными моментами
 ,
(5.11)
,
(5.11)
 .
(5.12)
.
(5.12)
Поскольку
все пакеты (5.8) адресованы дальше
 ,
то по пути до
,
то по пути до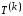 они имеют более высокий приоритет, чем
пакеты из
они имеют более высокий приоритет, чем
пакеты из .
.
Обозначим как
 (5.13)
(5.13)
и
 (5.14)
(5.14)
-
число всех пакетов в сети, которые на
своем пути до
 имеют более высокий приоритет, чем
пакеты от
имеют более высокий приоритет, чем
пакеты от к
к (с учетом адресованных в
(с учетом адресованных в ).
).
Пакеты
из (5.13), (5.14) на пути до
 не встречают более важных (ибо остальные
адресованы «ближе»), следовательно,
всегда ровно
не встречают более важных (ибо остальные
адресованы «ближе»), следовательно,
всегда ровно из них может достичь
из них может достичь и тем самым убыть из
и тем самым убыть из .
.
Следовательно,
 ,
(5.15)
,
(5.15)
Где
 ,
(5.16)
,
(5.16)
а
 независимы и одинаково распределены
при
независимы и одинаково распределены
при с производящей функцией
с производящей функцией
 (5.17)
(5.17)
и конечными моментами
 ,
(5.18)
,
(5.18)
 .
(5.19)
.
(5.19)
Пакеты
из потока
 могут занимать вSTM
(к моменту его прихода в
могут занимать вSTM
(к моменту его прихода в
 )
все места, не занятые пакетами из
)
все места, не занятые пакетами из - число таких мест равно
- число таких мест равно .
Следовательно,
.
Следовательно,
 .
(5.20)
.
(5.20)
Уравнения
типа (5.15) и (5.20), описывающие двумерную
цепь Маркова (  ,
,
 ),
где найдены стационарные распределения
обеих координат, В частности,
),
где найдены стационарные распределения
обеих координат, В частности,
 (5.21)
(5.21)
где
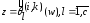 — решения уравнения вида (5.5):
— решения уравнения вида (5.5):
 .
.
Отсюда
в соответствии с (5.7), (5.18) получим среднее
время доставки пакета из
 .
.
Найдем
распределение
 для числа требований из
для числа требований из ,
находящихся на ожидании в пункте
,
находящихся на ожидании в пункте ,
после чего по формуле Литтла получим
среднее значение времени ожидания
,
после чего по формуле Литтла получим
среднее значение времени ожидания доступа
в канал пакета из
доступа
в канал пакета из :
:
 ,
(5.22)
,
(5.22)
поскольку
интенсивность поступления этих пакетов
равна
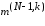 .
.
Доступу
в STM
пакета от пункта
 к пункту
к пункту препятствуют, во-первых, пакеты от более
ранних (по ходуSTM),
чем
препятствуют, во-первых, пакеты от более
ранних (по ходуSTM),
чем
 ,
пунктов, которые еще не миновали
,
пунктов, которые еще не миновали и адресованы дальше
и адресованы дальше ,
и, во-вторых, находящиеся на
,
и, во-вторых, находящиеся на на ожидании пакеты от
на ожидании пакеты от ,
адресованные далее
,
адресованные далее .
Обозначим их общее число через
.
Обозначим их общее число через .
.
Пакеты
из
 на своем пути до
на своем пути до не встречают других более важных,
следовательно, могут полностью загружатьSTM.
Таким образом,
не встречают других более важных,
следовательно, могут полностью загружатьSTM.
Таким образом,
 ,
(5.23)
,
(5.23)
где
 (5.24)
(5.24)
-
число пакетов, пополняющих
 )
в течение
)
в течение
 -го
такта и имеющих производящую функцию
-го
такта и имеющих производящую функцию
 (5.25)
(5.25)
и
конечные моменты
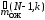 и
и ,
вычисляемые по формуле (5.24) заменой
,
вычисляемые по формуле (5.24) заменой на
на или соответственно на
или соответственно на .
.
Пакеты
из
 при проходеSTM
мимо пункта
при проходеSTM
мимо пункта
 могут занимать в нем все места, не занятые
пакетами из
могут занимать в нем все места, не занятые
пакетами из - число таких мест равно
- число таких мест равно .
Следовательно,
.
Следовательно,
 .
(5.26)
.
(5.26)
Решая совместно (3.23) и (3.26), так же, как и выше, получаем
 (5.27)
(5.27)
где
 – решения уравнения
– решения уравнения
 .
(5.28)
.
(5.28)
Теперь
из формулы (5.22) получим искомый результат.
Аналогичные соотношения выполняются
и для любой другой пары «вход-выход».
Отметим, что при
 в выражениях (5.21) и (5.27) отсутствует
последнее слагаемое, и, таким образом,
средние значения времени ожидания и
доставки определяются первыми двумя
моментами поступающей нагрузки.
в выражениях (5.21) и (5.27) отсутствует
последнее слагаемое, и, таким образом,
средние значения времени ожидания и
доставки определяются первыми двумя
моментами поступающей нагрузки.
