Методичка 6М

УДК 536.7(075.8) ББК В 317.1

Г 703

Рецензент:

Доцент кафедры «Физика»

Дальневосточного государственного университета путей сообщения

Л.Л. Коваленко

Гороховский В.Б.

Изучение некоторых термодинамических состояний газа.

Г703 Методические указания на выполнение лабораторной работы.

–Хабаровск: Изд-во ДВГУПС, 2000. – 14 с.: ил.

Методические указания составлены на выполнение лабораторной рабо- ты по разделу «Основы термодинамики». В теоретической части даны за- коны термодинамики и их применение к изопроцессам. Понятия удельной и молярной теплоемкостей и связь между ними, адиабатный процесс. Ука- зания содержат описание рабочей установки и метода лабораторного ис- следования. В заключительной части предусмотрено дополнительное за- дание для студентов, которые успешно справляются с основной задачей. Для защиты лабораторной работы приведены контрольные вопросы.

Указания предназначены для студентов первого курса всех технических специальностей дневной и заочной форм обучения.

УДК 536.7(075.8) ББК В 317.1

© Издательство Дальневосточного государственного университета путей сообщения (ДВГУПС), 2000

2

ВВЕДЕНИЕ

Метод молекулярно-кинетической теории является одним из способов изучения свойств вещества в газообразном, жидком и твердом состояниях, а также взаимных переходов из одного состояния в другое. Этот метод, применяемый для объяснения макроскопических свойств тел с точки зре- ния их молекулярного строения, есть по существу статистический.

Однако возможен и другой способ описания явлений, без детального рассмотрения тех микроскопических процессов, которые при этом проис- ходят. Такое описание можно сделать, исходя из понятий об энергии, ее превращениях и способах передачи.

Метод, рассматривающий процессы с энергетической точки зрения, на- зывается термодинамическим. С его помощью можно изучать свойства идеального и реального газов, упругость и сжимаемость, адсорбцию и диффузию, поведение вещества под действием давления и температуры, испарение и конденсацию, плавление, кристаллизацию и другие явления.

С помощью термодинамического метода решается множество вопросов в учении об электричестве, магнетизме, излучении и т. п. Он, кроме физики и химии, используется в ряде технических наук.

Весь этот широкий круг вопросов о свойствах энергии и законах ее пре- вращений, а также о процессах и состоянии равновесия в системах, в ко- торых наблюдаются тепловые эффекты, составляет предмет термодина- мики.

Среди многочисленных разделов современной физики термодинамика занимает особое положение. Это связано с тем, что любая форма энергии при ее превращениях в конце концов переходит в теплоту. В теплоту пере- ходит механическая энергия, энергия электрического тока, энергия света, энергия химической реакции и т. д. Любой вид энергии в процессе пре- вращений может пройти через многие формы энергии, но конечным ре- зультатом всех таких превращений непременно является теплота.

Наибольший практический интерес представляет превращение механи-

ческой энергии в теплоту и обратный процесс получения механической работы за счет теплоты.

При выполнении лабораторной работы студент изучает некоторые термодинамические состояния газа.

В рассматриваемой лабораторной работе даются основные положения термодинамики, подробно рассматривается теплоемкость газов при раз- личных условиях, применяется первое начало термодинамики к различ- ным изопроцессам, и изучается адиабатный процесс. Конечной целью ра- боты является определение показателя адиабаты.

3

ЦЕЛЬ РАБОТЫ

Определить отношение удельных теплоемкостей воздуха при постоян- ном давлении и постоянном объеме.

Приборы и принадлежности: стеклянный баллон с краном; жидкостный манометр; микрокомпрессор.

1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

1.1. Основные положения термодинамики

Термодинамикой называется раздел физики, в котором изучаются условия превращения энергии из одного вида в другой, и качественные соотношения при таких превращениях. В основе термодинамики лежат экспериментально установленные законы (начала) термодинамики. С по- мощью этих законов можно, не принимая во внимание молекулярное строение веществ, получить много сведений о свойствах тел и закономер- ностях процессов, происходящих с телами в различных условиях. Для

описания состояния термодинамической системы вводятся физические величины, называемые термодинамическими параметрами или парамет- рами состояния системы. Основными параметрами состояния системы яв- ляются: давление Р, удельный объем Vуд, занимаемый единицей массы вещества, и температура Т.

Для однородного тела удельный объем равен отношению его объема к массе:

Vуд= V/m.

Два состояния системы считаются различными, если для них неодина- ковы значения хотя бы одного из термодинамических параметров.

Состояние системы называется стационарным, если оно не изменяется со временем. Это означает, что ни один из термодинамических параметров, определяющих состояние, не изменяется с течением времени.

Равновесное состояние устанавливается в системе при постоянных внешних условиях и сохраняется в системе произвольно долго. Во всех частях системы, находящейся в состоянии термодинамического равнове- сия, температура одинакова. Температура равновесной системы является мерой интенсивности теплового движения ее молекул, то есть средней ки- нетической энергии.

Между тремя параметрами состояния системы существует связь, назы- ваемая уравнением состояния. Оно записывается в форме функциональ- ной зависимости давления в системе от объема и температуры.

4

Идеальным газом называется газ, молекулы которого не взаимодей- ствуют друг с другом на расстоянии и имеют исчезающе малые собст-

венные объемы. У реальных газов молекулы испытывают силы межмоле- кулярного взаимодействия притяжения и отталкивания. Уравнение состоя-

где p, V и T – давление, объем и абсолютная температура газа, R – уни- версальная газовая постоянная, численно равная работе, совершенной

одним молем идеального газа при изобарном повышении температуры на один градус:

где n – концентрация молекул газа, то есть число молекул в единице объ- ема газа; k – постоянная Больцмана, k = 1, 38×10-23 Дж/К.

1.2. Теплоёмкость газов

Одной из важнейших физических характеристик газов является тепло- емкость. Различают удельную и молярную теплоемкость.

Удельной теплоемкостью газов с называется величина, численно равная количеству теплоты, которое необходимо сообщить единице массы газа, чтобы увеличить его температуру на один градус.

Молярной (мольной) теплоемкостью Сμ называется величина, чис- ленно равная количеству теплоты, которое необходимо сообщить од- ному молю газа, чтобы увеличить его температуру на один градус:

где m – молярная масса газа.

Удельная и молярная теплоемкости газа зависят от условий, при кото- рых проводится нагревание, то есть от характера термодинамического процесса. Например, можно проводить нагревание при постоянном объе- ме или при постоянном давлении. Тогда получим соответственно теплоем- кость при постоянном объеме Сv или при постоянном давлении Сp. При этом всегда Сp > Сv.

5

Эта зависимость теплоемкости газов от условий нагревания может быть выяснена при использовании уравнения состояния идеального газа и первого начала термодинамики. Первое начало термодинамики формули-

руется так: количество теплоты dQ переданное системе, затрачивает- ся на увеличение ее внутренней энергии dU и на работу dА, совершае-

мую системой против внешних сил

где i – число степеней свободы молекулы газа, то есть наименьшее число координат, которое необходимо задать, чтобы определить положение мо- лекулы в пространстве.

Элементарная работа

Если при изменении температуры объем газа не меняется (V = const),

процесс называется изохорическим: V = const, dV = 0, dA = pdV = 0.

Все подводимое к газу тепло идет на увеличение его внутренней энер- гии. Тогда из уравнения (1.10) следует, что молярная теплоемкость при постоянном объеме газа равна:

Из уравнения состояния для одного моля газа pV = RT получаем pdV + Vdp = RdT.

Но р=const, dp = 0, следовательно,

pdV = RdT.

6

Формула (1.13) носит название уравнения Майера. Смысл уравнения Майера заключается в том, что при изобарическом нагревании газа на один градус к газу должно быть подведено большее количество теплоты, чем для такого же изохорического нагревания. Разность количеств теплот должна быть равна работе совершаемой газом при изобарическом расши- рении.

Теплоемкость вещества (при Т = const) в изотермическом процессе из определения, уравнение (1.9), равна бесконечности, так как dT = 0, а dQ ¹ 0, то С = ¥. При изотермическом процессе первое начало термоди-

намики имеет вид

так как при Т = const, dT = 0 и dU = 0, U = const. С точки зрения производ- ства работы газом, этот изопроцесс наивыгоднейший. Работа совершае- мая газом при Т = const:

где m/m – количество молей газа, содержащихся в массе m, Т – постоянная температура газа, V1 и V2 – начальный и конечный объем газа.

Из молекулярно-кинетической теории следует, что Сpμ и Сvμ зависят от числа степеней свободы i молекул, из которых состоит газ:

Молекула одноатомного газа имеет три степени свободы (i = 3), жест- кая молекула двухатомного газа – пять (i = 5), трехатомного и многоатом- ного – шесть (i = 6). Отсюда следует, что молекулярная теплоемкость це- ликом определяется природой газа. Отношение теплоемкости газа Сp к

Сv называется показателем адиабаты.

Для идеального газа

Величина γ играет очень большую роль в проведении термодинамичес- ких и газодинамических расчетов, в особенности таких, которые связаны с адиабатическими процессами.

1.3. Адиабатный процесс

Если быстро сжимать газ или предоставить ему возможность быстро расширяться, причем изменение объема газа осуществлять без теплооб- мена с окружающей его средой, то такой процесс изменения состояния га-

за называется адиабатическим (адиабата).

При адиабатическом сжатии изменяется не только объем и давление газа, как при изотермическом процессе, но также изменяется и температура. Это изменение температуры газа происходит вследствие того, что за счет работы, затрачиваемой на сжатие газа, увеличивается его внутренняя энергия. Сле- довательно, уменьшение объема газа при адиабатическом сжатии должно повлечь за собой большее, чем при изотермическом сжатии, увеличение дав- ления.

Примером адиабатного процесса может служить весьма быстрое рас- ширение в атмосферу газа, помещенного в теплоизолированный сосуд, при быстром открывании крана. Адиабатный процесс должен происходить на столько быстро, чтобы не успел произойти теплообмен газа с атмосфе- ры при открывании крана.

Согласно первому началу термодинамики, теплота сообщаемая рас-

ходуется на увеличение ее внутренней энергии и на совершение системой работы против внешних сил, то есть

dQ = dU +dA.

При адиабатическом процессе dQ = 0, следовательно, dA = -dU, то есть работа, совершаемая газом при расширении, осуществляется за счет уменьшения внутренней энергии вещества.

Адиабатический процесс подчиняется закону Пуассона

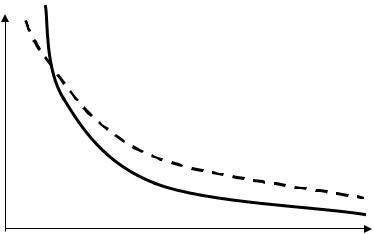
На рис. 1.1, на P – V диаграмме, сплошной линией изображена кривая, опи- сывающая адиабатическое сжатие. На этом же рисунке пунктиром показана изотерма, соответствующая температуре газа в начальном состоянии. Из ри- сунка видно, что адиабата идет круче, чем изотерма.

При помощи адиабатического процесса с той или иной степенью приб- лижения можно рассматривать широкий круг практических задач. К их числу относятся следующие задачи:

– нахождение скорости распространения звука в газах;

8

– течение газа по входным устройствам компрессоров, турбинах и соплах реактивных двигателей и т.д.

P

V

Рис.1.1. Сравнение графиков изотермического и адиа-

батического процессов

В табл.1.1 приведены сводные данные о характеристиках изопроцессов в газах.

Таблица 1.1

Сводные данные о характеристиках изопроцессов в газах

2. МЕТОД РАБОТЫ

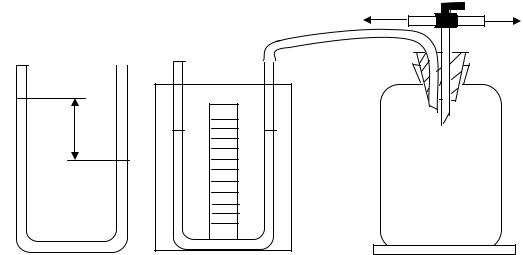
2.1. Лабораторная установка

Экспериментальная установка (рис.2.1) состоит из стеклянного балло- на достаточно большой емкости, соединенного с жидкостным U-образным манометром. Верхняя часть баллона закрыта пробкой и снабжена краном,

с помощью которого баллон сообщается с атмосферой и источником давления (в данном случае микрокомпрессором).

атмосфера

к микро-

компрессору

h

Рис. 2.1. Общий вид установки для определения величины отношения

γ =СP/CV

2.2. Метод измерения

Пусть в баллоне первоначально было атмосферное давление Pа. Если быстро повысить давление в баллоне и закрыть кран, то окончатель- ная разность уровней в манометре h1 установится не сразу (при быстром сжатии температура газа в баллоне повысится и пройдет некоторое время, пока температура воздуха в баллоне не сравняется, за счет теплопровод- ности, с температурой окружающего воздуха).

При всех дальнейших наблюдениях надо мысленно выделить в сосуде некоторую массу воздуха объемом V и рассматривать изменения, проис- ходящие только с этим количеством воздуха.

Предположим, что происходящие с газом изменения изображены на графике, выражающем зависимость P от V (рис.2.2).

Обозначим температуру окружающего воздуха То, а через Р1 – давле- ние газа внутри баллона.

10