Геометрические построения в задаче 11 б

Словесная форма	Графическая форма
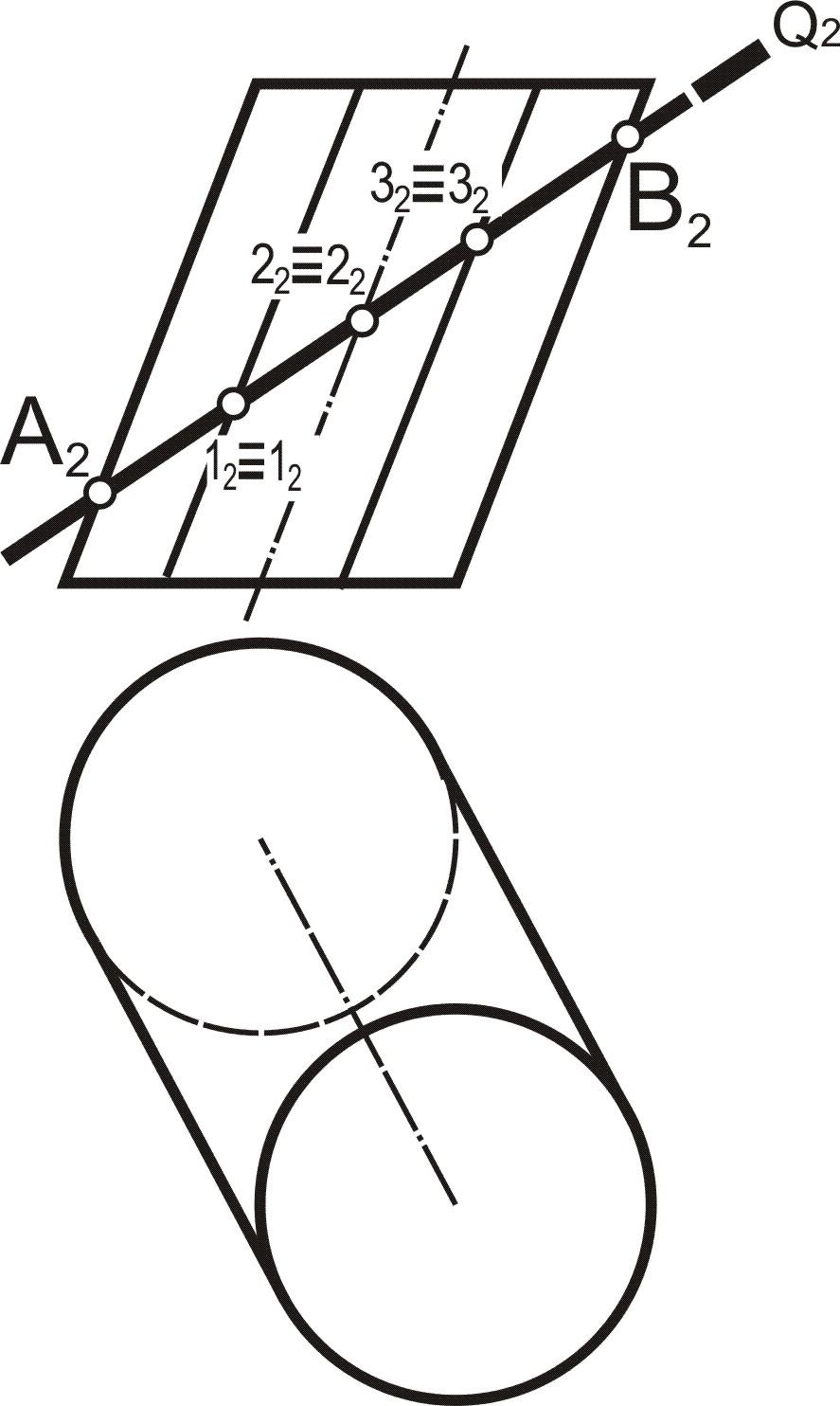
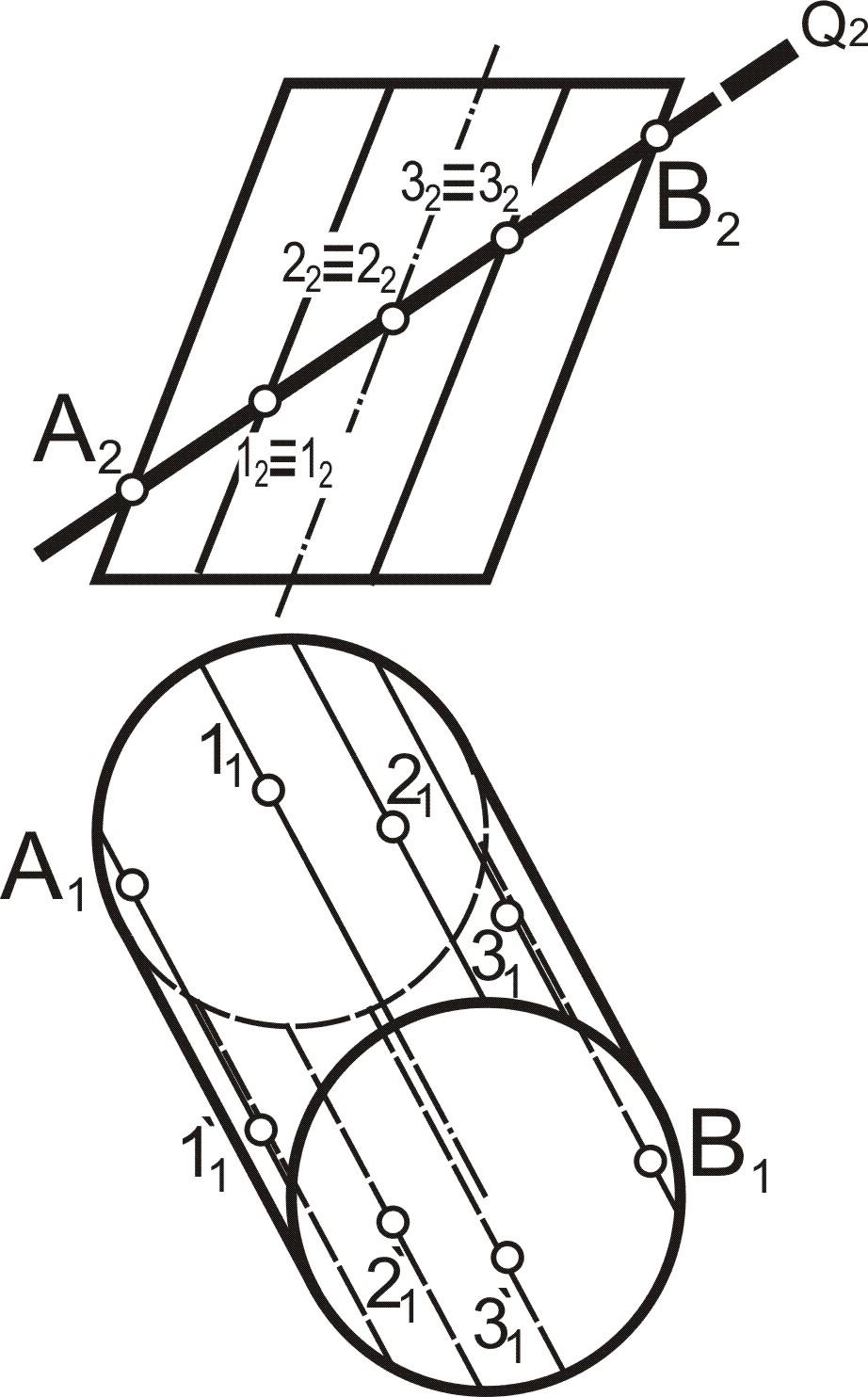
1. Отметить характерные A и B: (A2, B2) и промежуточные 1 и 1`, 2 и 2`, 3 и 3` (12, 1`2, 22, 2`2 ,32, 3`2) точки, принадлежащие линии пересечения плоскости Q с цилиндрической поверхностью
2. Построить горизонтальные проекции точек A, B, 1 …3 и 1`…3` при помощи образующих боковой поверхности цилиндра

Окончание табл. 7.6

Словесная форма	Графическая форма
3. Соединить последовательно точки A1, B1, 11…31 и 11`…31` . Отвести проекцию линии сечения с учетом видимости

4. Найти натуральную величину сечения методом вспомогательных секущих плоскостей (рис. 7.25):

–

Рис. 7.25. Определение натуральной величины сечения цилиндрической поверхности плоскостью методом замены плоскостей проекций

задать новую систему плоскостей П₂П₄, где осьx` – линия пересечения плоскостей проекций П₂П₄;

– из точек A₂,B₂, 1₂…3₂провести перпендикуляры к осиx`;

–  на оси x` отметить точкиA_x,B_x, 1_x…3_x ;

–  из точек A_x,B_x, 1_x…3_xна перпендикулярах отложить расстояние, равное удаленности точекA,B, 1 …3 и 1`…3` от горизонтальной плоскости проекций П₁;

– соединить все полученные точки линией.

Полученный эллипс – это натуральная величина сечения данной поверхности плоскостью Q.

Задача 12 а. Даны призматическая поверхность, прямаяl.

Построить точки пересечения поверхности и прямой l и определить видимости прямой относительно точек пересечения.

Алгоритм решения.

1. Выполнить анализ условия задачи. Определить признаки понятий: «гранная поверхность», «призматическая поверхность», «прямая», «пересечение гранной поверхности прямой общего положения».

2. Определить алгоритм решения исходя из общего алгоритма определения точек пересечения прямой общего положения и поверхности.

3. Выполнить построения (рис. 7.26):

3

Рис. 7.26. Геометрические построения к задаче 12 а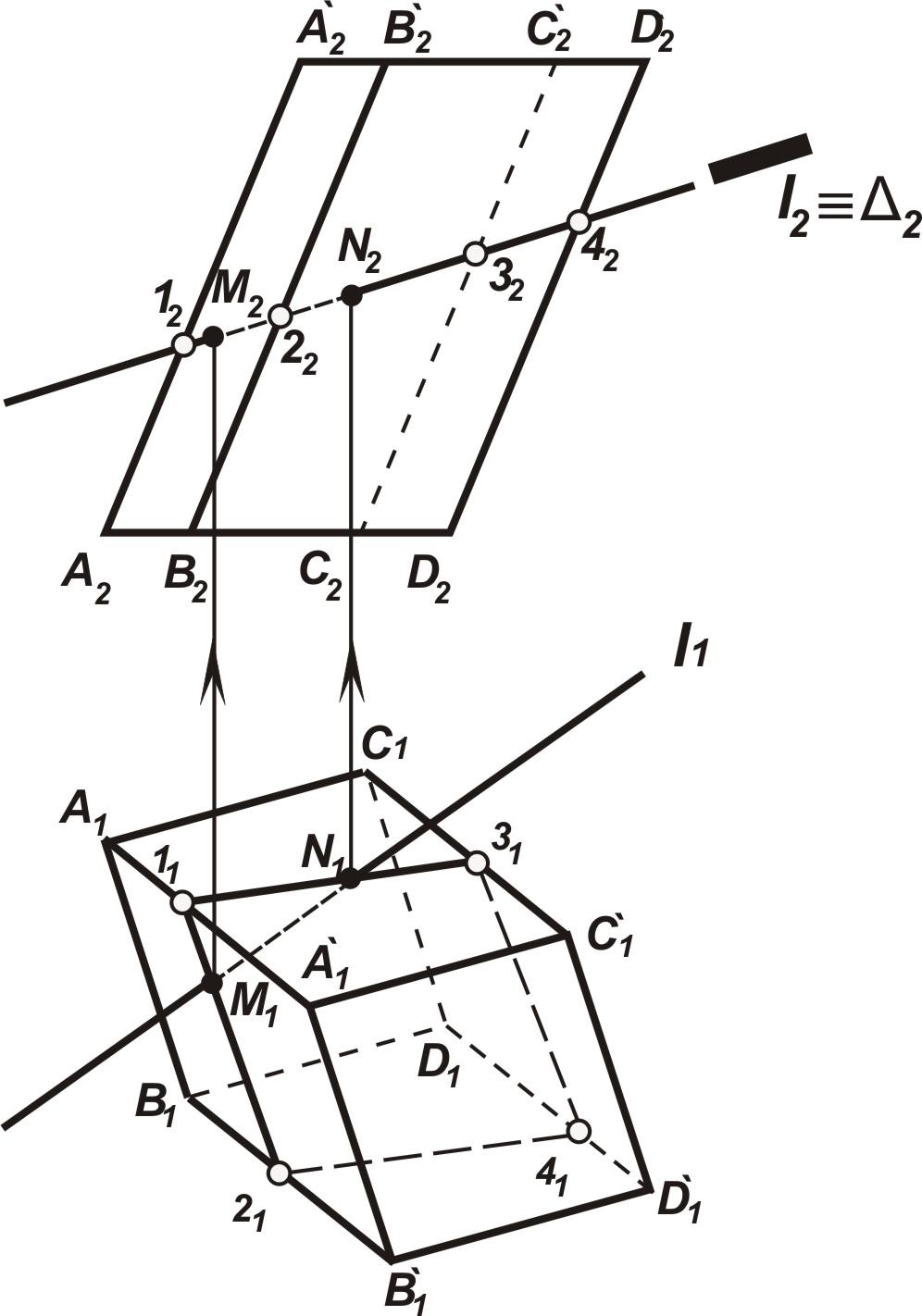

.1. Заключить l во вспомогательную плоскость Δ.

3.2. Определить точки 1₂, 2₂, 3₂, 4₂, которые являются точками пересечения плоскости Δ₂ с ребрами граней данной призмы и принадлежат линии пересечения этой плоскости с пирамидой.

3.3. Определить горизонтальные проек­ции точек 1, 2, 3, 4 (точки 1₁, 2₁, 3₁, 4₁). 1ΠAA`Þ1<sub>1</sub>ΠA<sub>1</sub>A`₁; 2ΠBB`Þ 2<sub>1</sub>ΠB<sub>1</sub>B`₁; 3Î CC` Þ Þ 3<sub>1</sub>Î C<sub>1</sub>C`₁; 4Î DD`Þ4<sub>1</sub>Î D<sub>1</sub>D`₁. Попарно соединить точки, принадлежащие одной грани с учетом видимости. Линия (1-2-3-4) = =ABCDA`B`C`D`∩Δ .

3.4. l∩ABCD A^{`</sup>B<sup>`}C^{`</sup>D<sup>`}(1-2-3-4) = M,N,определить точки M и N: MÎ 1-2 Þ M₁Î 1₁-2₁; NÎ 1-2 Þ N₁Î 2₁-3₁; MÎ 1-2 Þ M₂Î 1₂-2₂; NÎ 1-2 ÞN₂Î 2₂-3₂. Показать видимость прямойl.

Задача 12 б. Даны коническая поверхность и прямая l.

Построить точки пересечения поверхности и прямой l и определить видимости прямой.

Алгоритм решения.

1. Выполнить анализ условия задачи. Определить признаки понятий: «поверхность», «коническая поверхность», «прямая», «пересечение кони­ческой поверхности прямой общего положения».

2. Определить алгоритм решения исходя из общего алгоритма опре­деления точек пересечения прямой общего положения и поверхности.

3. Выполнить построения (рис. 7.27).

3.1. Заключить прямую l во вспомогательную плоскость Σ.

3.2. Отметить характерные точки 1₂, 3₂, 3`₂ 5₂, принадлежащие линии пересечения плоскости Σ с конусом.

3.3. Построить горизонтальные проекции точек 1, 3, 3`, 5 (точки 1<sub>1</sub>, 3<sub>1</sub>, 3`₁ 5₁) с помощью образующих. Точки 1 и 5 лежат на крайних образующих конуса. Построить горизонтальные проекции крайних образующих. Опустить перпендикуляры линий связи из точек 1₂ и 5₂ до пересечения с соответствующей образующей. Точки 3 и 3` найти таким же образом.

Рис. 7.27. Геометрические построения к задаче 12 б

3.4. Кроме характерных точек линии пересечения конуса и плоскости Σ, необходимо построить ряд промежуточных точек. К примеру, точки 2 ,2`, 4 и 4`. Эти точки можно определить также при помощи образующих.

4. Соединить точки 1₁, 2₁, 2`<sub>1</sub>, 3<sub>1</sub>, 3`1, 4₁, 4`₁, 5₁ с учетом видимости.

5. Определить точки M и N. Сначала найти точки M₁и N₁там, где прямая l пересекла линию пересечения. Построить фронтальные проекции точек M и N. Показать видимость прямойl.

 Рекомендуемый библиографический список [2–11].