Геометрические построения в задаче 8 в

Словесная форма	Графическая форма
1. Ввести первую систему плоскостей П1П4: ось x` – ось пересечения плоскостей проекций П1П4 – параллельно проекциям прямых, OX`IIА1В1. Перпендикулярно оси OX` провести линии связи из точек A1, B1, D1
2. На линиях связи от оси OX` отложить расстояния удаленности точек A, B, D до горизонтальной плоскости проекций П1: IA2AxI=IAx`A4I, IB2BxI=IBx`B4I, ID2DxI=IDx`D4I
3. Ввести вторую систему плоскостей П4П5: ось OX`` перпендикулярна проекциям А4В4. 4. На линиях связи от оси OX`` отложить расстояния удаленности точек A, B, D до плоскости проекций П4: IA1Ax`I=IA4Ax`I = = IB1Bx`I=IB4B4`I, ID1Dx`I=ID4Dx`I. Проекция АВ на плоскости П5 проецируется в точку: А5=В5. A5D5 – искомое расстояние

3.1. Выполнить первую замену плос­костей П₁П₄и преобразовать отрезки прямой линииABв прямую уровня. Провести осьx`– ось пересечения плоскостей проекций П<sub>1</sub>П<sub>4</sub>, параллельно проекции прямойAB,OX`IIA₁B₁. Перпендикулярно осиOX` провести линии связи из точекA<sub>1</sub>,B<sub>1</sub>,C<sub>1</sub>,D<sub>1</sub>. На линиях связи от оси OX` отложить расстояния удаленности точекA,B,C,Dдо плоскости проекций П₁. Полученные проекции точек соединить:A₄сB₄,C₄сD₄(рис. 6.23).

3.2. Выполнить вторую замену плоскостей П₄П₅ и преобразовать отрезок прямой линии уровняABв проецирующую прямую. Провести осьx`` – ось пересечения плоскостей проекций П<sub>4</sub>П<sub>5</sub> – перпендикулярно линии связи от проекции A<sub>4</sub>B<sub>4</sub>. Провести линии связи от А<sub>4</sub>В<sub>4</sub>. На линиях связи от оси OX`` отложить расстояния удаления точек A, B, C, D до плоскости проекций П₄. Отрезок AB на плоскость П₅ проецируется в точку: A₅ = B₅ = N₅. Построить из точкиN₅перпендикуляр кC₅D₅:M₅N₅^C₅D₅ (рис. 6.24).

Рис. 6.23. Первая замена плоскостей

Рис. 6.24. Вторая замена плоскостей

Задача 8 в. Дан отрезок прямой линии общего положения АВ, точкаD(рис. 6.25).

Методом замены плоскостей проекций определить расстояние между прямой и точкой.

Алгоритм решения.

1

Рис. 6.25

. Выполнить анализ условия задачи. Определить признаки понятия: «расстояние между точкой и прямой».

2. Определить алгоритм решения исходя из следующего:

– необходимо выполнить преобразование прямой общего положения в прямую уровня;

– необходимо преобразовать прямую уровня в проецирующую.

3. Выполнить построения согласно алгоритму (табл. 6.3).

Задача 8 г. Дан двугранный уголABCD(рис. 6.26).

Методом замены плоскостей проекций определить натуральную величину двугранного угла.

А

Рис. 6.26

лгоритм решения.

1. Выполнить анализ условия задачи. Определить признаки понятий: «двугранный угол», «измерение углов».

2. Определить алгоритм решения исходя из следующего:

– необходимо выполнить преобразование ребра двугранного угла – прямую общего положения в прямую уровня;

– необходимо преобразовать прямую уровня в проецирующую.

3. Выполнить построения согласно алгоритму.

3.1. Выполнить первую замену плоскостей П₁П₄и преобразовать ребро двугранного углаABв прямую уровня (рис. 6.27). Провести осьx`– ось пересечения плоскостей проекций П<sub>1</sub>П<sub>4</sub>– параллельно проекциям прямых,OX`IIА₁В₁. Перпендикулярно оси OX` провести линии связи из точек A<sub>1</sub>, B<sub>1</sub>, C<sub>1</sub>, D<sub>1</sub>. На линиях связи от оси OX` отложить расстояния удаленности точекA,B,C,Dплоскости проекций П₁. Построить проекцию двугранного угла на плоскости П₄,A₄B₄,C₄D₄.

3.2. Выполнить вторую замену плос­костей П₄П₅ и преобразовать ребро двугранного углаABиз линии уровня в проецирующую прямую (рис. 6.28). Провести осьOX``перпендикулярно проекциям А<sub>4</sub>В<sub>4</sub>. На линиях связи от оси OX`` отложить расстояния удаленности точекA,B,C,Dдо плоскости проекций П₄. Построить проекцию угла на плоскости П₅: грани угла проецируются в прямые линии, а ребро АВ – в точку. Уголпроецируется в плоскости П₅в натуральную величину.

Рис. 6.27. Первая замена плоскостей	Рис. 6.28. Вторая замена плоскостей

З

Рис. 6.29

адача9. Дана плоскость Р(АВС) (рис. 6.29).

Методом плоскопараллельного перемещения или вращением вокруг проецирующей прямой определить расстояние от точки до плоскости.

Алгоритм решения.

1. Выполнить анализ условия задачи. Определить признаки понятий «плоскость», «плоскопараллельное перемещение», «расстояние от точки до плоскости».

2. Определить алгоритм решения исходя из следующего:

– необходимо преобразовать данную плоскость общего положения в проецирующую (рис. 6.30);

– необходимо преобразовать проецирующую плоскость в плоскость уровня.

3. Выполнить построения согласно алгоритму.

3.1. В плоскости Р(∆АВС) построить горизонталь h(h₁h₂).

3.2. Переместить горизонтальную проекцию плоскости так, чтобы её горизонталь стала перпендикулярна П₂, при этом ∆А₁В₁С₁и ∆А΄₁В΄₁С΄₁ соразмерны.

3.3. Построить фронтальную проекцию фронтально проецирующей плоскости Р΄, которая выродится в прямую А΄₂В΄₂С΄₂.

3.4. Построить проекции точки D΄ – D΄₁ и D΄₂.

3.5. Из точки D΄₂построить перпендикуляр к Р΄₂.

3.6. Построить точку К΄₁, затем К₁и К₂.

3.7. Соединить одноименные проекции точек D и Κ. Отрезок D΄Κ΄llП₂, следовательно, D΄₂Κ΄₂– натуральная величина и определяет расстояние от точки D до плоскости Р.

Рис. 6.30. Геометрические построе­ния в задаче 9

З

Рис. 6.31

адача 10. Дана плоскость Р(АВС) (рис. 6.31).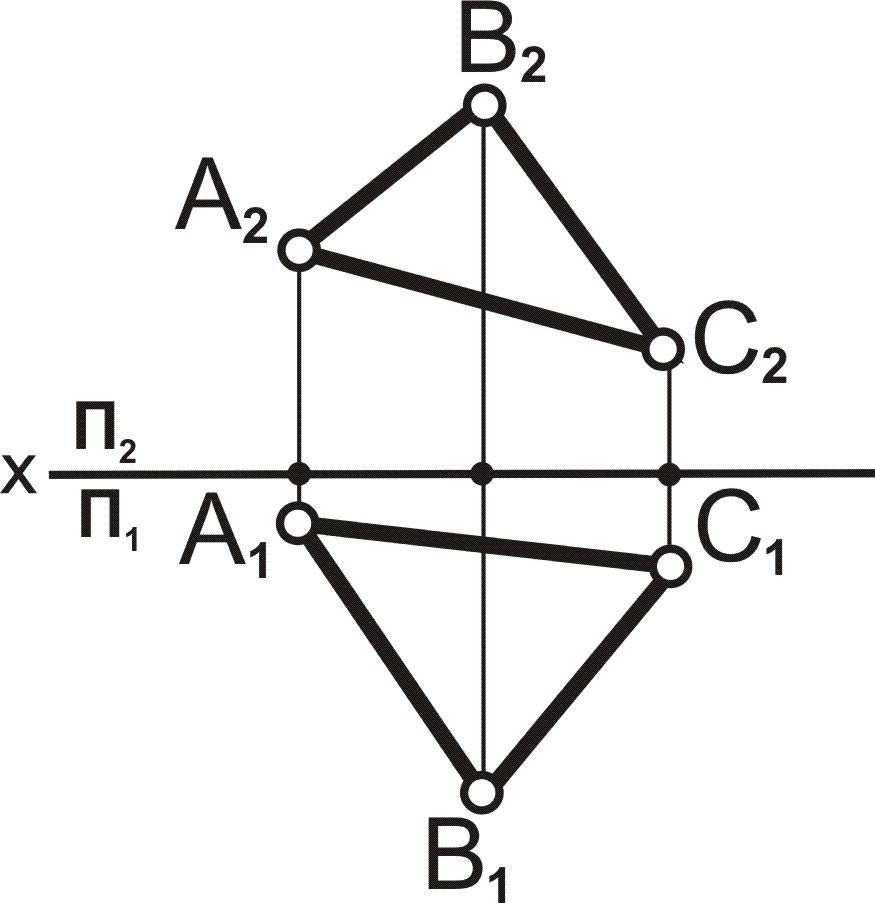

Методом вращения вокруг горизонтали (либо фронтали) определить натуральную величину треугольника.

Алгоритм решения.

1. Выполнить анализ условия задачи. Определить признаки понятий: «плоскость», «горизонталь», «вращение вокруг горизонтали».

2. Определить алгоритм решения:

– необходимо провести горизонталь плоскости Р(АВС);

– необходимо использовать метод прямоугольного треугольника для определения радиуса вращения.

2. Выполнить построения согласно алгоритму (табл. 6.4).

Таблица 6.4