1.4. Решение инженерных задач по топографическим картам

1.4.1. Определение географических координат точек

Географическая широта– угол, образованный отвесной линией в данной точке и экваториальной плоскостью (рис. 7).

Географическая долгота– двугранный угол между плоскостями меридиана данной точки с плоскостью начального меридиана (рис. 7).

Д

Рис. 7. Система географических координат

ля определения географических координат точки используют минутную рамку карты и значения долготы и широты, подписанные в углах рамки. Из заданной точки к ближайшим сторонам минутной рамки с помощью прямоугольного треугольника опускают перпендикуляры (рис. 8.) и измеряют линейкой отрезки.

Широту и долготу заданной точки получают из выражений

где – широты южной и северной параллелей, проходящих через границы минутного деления рамки;– расстояние вмм от точки до южной параллели; – расстояние вмм от точки до северной параллели; – долготы западного и восточного меридианов, проходящих через границы минутного деления рамки;– расстояние вмм от точки до западного меридиана;.– расстояние вмм от точке до восточного меридиана.

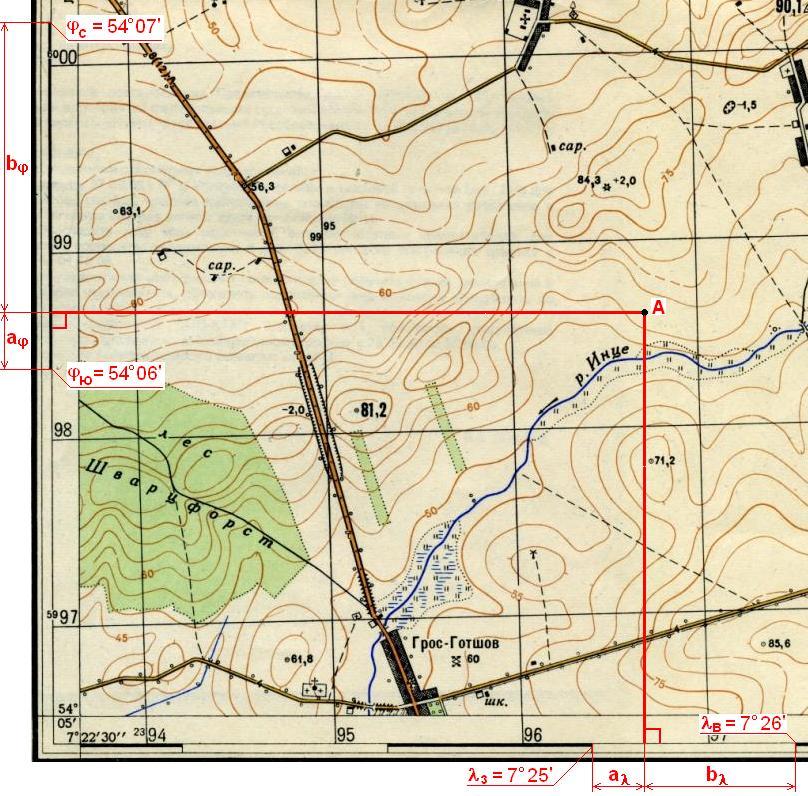
Рис. 8. Определение географических координат

В примере на рис. 8

1.4.2. Определение прямоугольных координат точек

Система прямоугольных координат представлена на карте километровой сеткой, образованной равноотстоящими линиями X и Y. При составлении топографических карт поверхность Земли меридианами через 6° делят на 60 зон, которые нумеруют, начиная от Гринвичского меридиана в направлении с запада на восток. Каждую зону изображают на плоскости, используя проекцию Гаусса, и устанавливают в ней прямоугольную систему координат, направляя ось Xна север по осевому меридиану зоны, а осьY– на восток по экватору. Линии абсциссXи ординатYна выходах за внутреннюю рамку карты подписывают значениями, выраженными в километрах (см. рис. 3). При этом у крайних линий сетки значения координат подписывают полностью – 5997 и 6006, а у промежуточных линий только две последние цифры 98, 99 и т.д.

Прямоугольные координаты точки определяют, используя километровую сетку и оцифровку её линий у внутренней рамки. Для этого находят координаты углов квадрата, в котором расположена точка, и измеряют кратчайшие расстояния от заданной точки до всех сторон квадрата (рис. 9).

Абсциссу и ординату точки рассчитывают по формулам

,

,

где – абсциссы южной и северной сторон квадрата, в котором расположена точка;– кратчайшее расстояние вмм от точки до южной стороны квадрата; – кратчайшее расстояние вмм от точки до северной стороны; – ординаты западной и восточной сторон квадрата;,– кратчайшие расстояния вмм от точки до западной и восточной сторон квадрата.

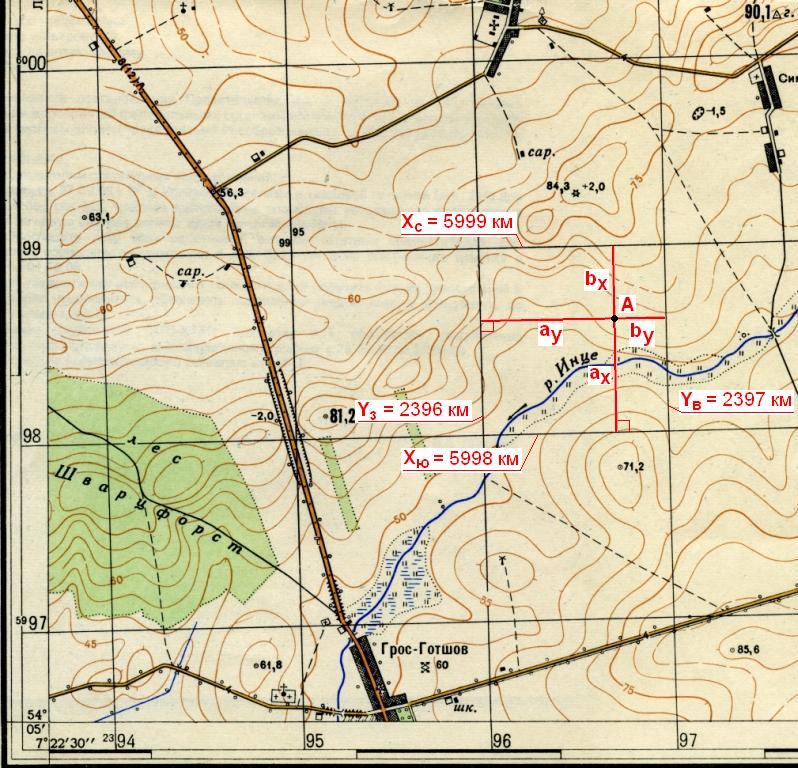
Рис. 9. Определение прямоугольных координат

В примере на рис. 9

,

.

1.4.3. Решение обратной геодезической задачи

Целью решения обратной геодезической задачиявляется вычисление длины линии и дирекционного угла линии по известным координатам её конечных точек. Т.е. при известных координатах точекА (X_A, Y_A) иВ (X_B, Y_B) необходимо найти длинуS_ABи направление линииАВ: осевой румбr_ABи дирекционный угол_AB(рис. 10).

Координаты точек А (X_A, Y_A) иВ (X_B, Y_B) определяют при решении предыдущей задачи (см. п.1.4.2).

Данная задача решается следующим образом.

Сначала находим приращения координат

ΔX = X_B – X_A ,

ΔY = Y_B – Y_A .

Рис. 10. Обратная геодезическая задача

Величину осевого румба r_AB определяем из отношения

.

По знакам приращений координат определяем четверть, в которой располагается румб, и её название (см. табл.1).

Таблица 1