Тема 3	Особенности потребительского выбора с учетом начального запаса
2.1	Эффекты дохода и замещения по Е. Слуцкому и Дж. Хиксу в коэффициентах эластичности
2.2	Выбор потребителя при наличии начального запаса. Уравнение Слуцкого с учетом начального запаса

Тема 2. Особенности потребительского выбора с учетом начального запаса

Эффекты дохода и замещения по Е. Слуцкому и Дж. Хиксу в коэффициентах эластичности

_{Используем уравнение бюджетной линии} , в которое подставим объемы продуктов из оптимального набора потребителя . Тогда

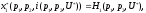_(2.1)

_{Запишем частную производную функции спроса (2.1) по переменной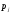} . (2.2)

_{Индексы цен и объемов продуктов принимают значения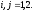} Согласно лемме Шепарда . Подставим это равенство в выражение (2.2). Получим первую версию уравнения Слуцкого:

(в общем случае ) (2.3)

_{так как} и

_{Продифференцируем утверждение леммы Шепарда по переменной} , получим выражение . В связи с тем, что , имеем т.е.

В общем случае 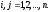Это вторая версия уравнения Слуцкого.

Матрица из вторых частных производныхназывается матрицей Слуцкого. Все ее элементы по главной диагонали отрицательны 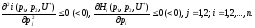Отрицательное значение означает с точки зрения функций спроса по Хиксу, что все продукты являются нормальными товарами.

Разделим обе стороны уравнения Слуцкого на и умножим на , получим . Преобразуем последнее слагаемое следующим образом: 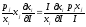, получим уравнение:

(2.4)

в котором - перекрестная эластичность спроса (по Маршаллу) на -й продукт по цене -го продукта . Если , получим прямую (обычную) ценовую эластичность спроса (по Маршаллу) на -й продукт по цене ; - перекрестная эластичность спроса по Хиксу на -й продукт по цене -го продукта . Если , получим прямую (обычную) ценовую эластичность спроса (по Хиксу) на -й продукт по цене ; - эластичность спроса по доходу;

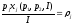- доля дохода потребителя, который он тратит на покупку -го продукта.

В коэффициенте отражается прямая зависимость ценовой эластичности спроса по Маршаллу от соотношения , от степени удовлетворения потребностей. Если цена высокая, то многие потребители не имеют возможности приобрести благо в желаемом количестве и объем покупок невелик, а потребность в товаре не насыщена. Поэтому даже небольшое снижение цены вызывает большое увеличение спроса, коэффициент высок. И наоборот. Когда цена низкая, объем покупок велик, большинство потребителей удовлетворяют свою потребность в продукте. Поэтому снижение цены вызывает незначительное изменение спроса на товар и коэффициент эластичности низкий.

Эластичность спроса по доходу находится в обратной зависимости от степени насыщения потребности в товаре. По необходимым благам степень насыщения потребности высока, поэтому с ростом дохода потребление таких товаров увеличивается незначительно, доход растет относительно быстрее, чем их потребление. Поэтому коэффициент эластичности по доходу 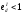. Потребность значительной части населения в высококачественных дорогих товарах удовлетворяется в небольшой степени, поэтому значительная часть прироста дохода используется на приобретение таких товаров. Поэтому, .

Таким образом, уравнение Слуцкого может быть представлено в эластичностях:

. (2.5)

Используем коэффициент ценовой эластичности спроса в решении одной из практических задач, которую нередко решают предприниматели. Валовой доход продавцов (выручка) равна _. Так как объем продаж или величина спроса зависит от цены товара, то. Продифференцируем функцию валового дохода по цене продукта, выполним преобразования и получим 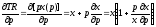. Так как , то . Принимая во внимание, что объем спроса всегда положителен или равен нулю, а ценовая эластичность спроса для нормальных товаров величина отрицательная, то

. (2.6).

Если , то выражение (2.6) будет отрицательным. Это означает, что цена и валовой доход изменяются в разных направлениях: если цена снижается, то валовой доход растет; если цена повышается, то доход уменьшается. Если , то выражение (2.6) будет положительным. В таком случае, если цена снижается, то валовой доход уменьшается; если цена растет, то доход увеличивается.

Валовой доход изменяется не только при изменении цены товара, но и изменении объема продаж. Проанализируем изменение валового дохода в случае изменения объемов продаж. Запишем обратную функцию спроса . Для этого продифференцируем выражение , выполним преобразования и получим . Предлагаем студенту магистратуры самостоятельно проанализировать, как изменяется валовой доход производителя при постоянной цене товара и изменяющемся объеме продаж.

Теоретические выводы анализа влияния изменения цены товара и объема продаж на изменение валового дохода фирмы при существующем значении ценовой эластичности спроса можно применять в решении соответствующей практической задачи в рамках дискретного анализа. Для этого используют значения всех параметров на дуге: . Фирмы располагают первичным фактическим материалом, позволяющим выполнить соответствующие расчеты.