
5.3. Полезность фон Неймана-Моргенштерна
В анализе поведения потребителя фон Неймана-Моргенштерна совместно используется теория полезности и теория вероятности. Она основана на аксиомах о вероятностной совокупности наборов товаров. В результате обосновывается функция полезности, обладающая измерительными свойствами, которые можно использовать в процессе принятия решений в условиях риска. Такие функции называются функциями полезности фон Неймана-Моргенштерна.
Основным
понятием рассматриваемой теории
полезности является лотерея, которая
определяется как множество наборов,
каждый из которых может быть получен с
заданной вероятностью. Так, набор
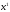 может быть получен с вероятностью
может быть получен с вероятностью
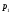 ,
набор
,
набор
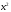 - с вероятностью
- с вероятностью
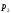 ,
…, набор
,
…, набор
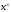 - с вероятностью
- с вероятностью
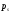 .
Лотерею представим в виде:
.
Лотерею представим в виде:
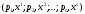 ,
где
,
где
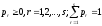 .
Если набор
.
Если набор
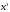 выигрывает наверняка, то лотерея
выигрывает наверняка, то лотерея
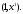 Если лотерея
Если лотерея
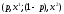 ,
то набор
,
то набор
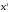 выигрывает с вероятностью
выигрывает с вероятностью
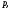 а набор
а набор
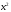 с вероятностью
с вероятностью
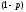 .
.
Согласно
первой аксиоме полезности фон
Неймана-Моргенштерна предполагается
существование отношения предпочтения,
которое является совершенной
полуупорядоченностью всех лотерей,
является совершенным, транзитивным и
рефлексивным. Безразличие ( ̴ ) и строгое
предпочтение
( )
определены здесь так же, как и в теории
потребительского поведения.
)
определены здесь так же, как и в теории
потребительского поведения.
Аксиома
монотонности состоит в следующем. Даны
два набора
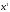 и
и
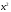 ,
для которых
,
для которых
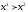 ;
тогда
;
тогда
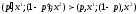 ,
если и только если
,
если и только если
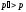 .
Это означает, что потребитель отдает
предпочтение лотерее с большей
вероятностью получить предпочитаемый
набор. Набор, который получают наверняка,
т.е.
.
Это означает, что потребитель отдает
предпочтение лотерее с большей
вероятностью получить предпочитаемый
набор. Набор, который получают наверняка,
т.е.
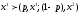 для всех
для всех
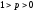 ,
предпочтительнее любой лотереи,
содержащей его и менее предпочтительный
набор.
,
предпочтительнее любой лотереи,
содержащей его и менее предпочтительный
набор.
Аксиома
непрерывности утверждает, что, если
даны три набора
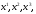 для которых
для которых
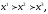 тогда существует вероятность
тогда существует вероятность
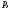 для которой
для которой
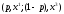 ̴
̴
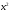 ,
где
,
где
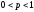 .
Т.е. выбранные лотереи интерполируют
между предпочтениями в том смысле, что
потребитель не делает различий между
лотереей, содержащей более предпочтительный
и менее предпочтительный наборы, и
определенностью получения некоторого
набора, занимающего промежуточное
положение.
.
Т.е. выбранные лотереи интерполируют
между предпочтениями в том смысле, что
потребитель не делает различий между
лотереей, содержащей более предпочтительный
и менее предпочтительный наборы, и
определенностью получения некоторого
набора, занимающего промежуточное
положение.
Аксиома
о независимости не связанных между
собой альтернатив отмечает: если заданы
два набора
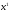 и
и
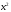 ,
для которых
,
для которых
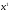 ̴
̴
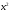 ,
тогда для любого третьего набора
,
тогда для любого третьего набора
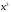 справедливо
справедливо
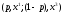 ̴
̴
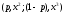 ,
для всех
,
для всех
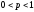 .
Присутствие третьего набора не нарушает
предпочтений.
.
Присутствие третьего набора не нарушает
предпочтений.
Аксиома
о приведении сложных лотерей. Дано
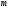 лотерей:
лотерей:
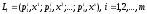 .
Рассмотрим сложную лотерею
.
Рассмотрим сложную лотерею
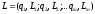 ,
под которой имеется в виду лотерея, в
которой в качестве исходов также
выступают лотереи, а
,
под которой имеется в виду лотерея, в
которой в качестве исходов также
выступают лотереи, а
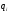 - вероятность получить лотерею
- вероятность получить лотерею
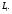 Согласно аксиоме сложная лотерея может
быть приведена к лотерее с подходящими
вероятностями
Согласно аксиоме сложная лотерея может
быть приведена к лотерее с подходящими
вероятностями
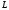 ̴
̴
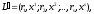
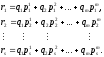
Основная
теорема теории полезности фон
Неймана-Моргенштерна утверждает, что
при соблюдении названных аксиом
существует функция полезности,
определенная на всех лотереях, являющаяся
однозначной с точностью до монотонного
строгого возрастающего линейного
преобразования. Так как одним из особых
видов лотереи является набор, где
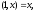 то
функция полезности определена для всех
наборов. При этом
то
функция полезности определена для всех
наборов. При этом
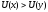 ,
если и только если
,
если и только если
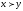 .
В общем виде
.
В общем виде
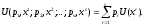 Последнее означает, что полезность
лотереи есть математическое ожидание
полезности, равное взвешенной сумме
полезностей наборов компонент, где в
качестве весов выступают вероятности.
Последнее означает, что полезность
лотереи есть математическое ожидание
полезности, равное взвешенной сумме
полезностей наборов компонент, где в
качестве весов выступают вероятности.
Функция
полезности фон Неймана-Моргенштерна
является однозначной с точностью до
монотонного строгого возрастающего
линейного
преобразования
в противоположность обыкновенным
функциям полезности, которые являются
однозначными с точностью до монотонного
строгого возрастающего (линейного или
нелинейного) преобразования. Таким
образом, если
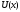 - функция полезности, то
- функция полезности, то
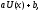 где
где
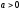 ,
также является функцией полезности.
Построим такую функцию полезности.
Выберем числовые значения для двух
уровней полезности; полезности других
наборов оценивают соответствующим
взвешиванием вероятностями. Допустим
,
также является функцией полезности.
Построим такую функцию полезности.
Выберем числовые значения для двух
уровней полезности; полезности других
наборов оценивают соответствующим
взвешиванием вероятностями. Допустим
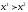 и
и
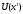 и
и
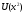 - произвольные числа, для которых
- произвольные числа, для которых
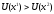 .
Они характеризуют уровни полезности
.
Они характеризуют уровни полезности
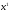 и
и
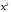 соответственно. Например,
соответственно. Например,
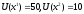 .
Чтобы определить полезность любого
другого набора, взвесим эти значения
полезностей вероятностями. Если
.
Чтобы определить полезность любого
другого набора, взвесим эти значения
полезностей вероятностями. Если
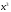 - набор, для которого
- набор, для которого
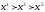 ,
то по аксиоме непрерывности существует
вероятность
,
то по аксиоме непрерывности существует
вероятность
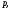 для которой выполняется
для которой выполняется
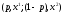 ̴
̴
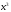 ,
(5.1)
,
(5.1)
поэтому
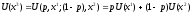 .
.
Первое равенство вытекает из того, что безразличные лотереи имеют одинаковые значения полезности. Второе равенство получено из определения полезности лотереи как математического ожидания ее полезности.
Допустим,
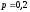 обеспечивает выполнение условия (5.1).
Тогда
обеспечивает выполнение условия (5.1).
Тогда
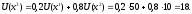
Аналогично,
если для
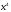 выполняется условие
выполняется условие
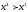 ,
то по аксиоме непрерывности существует
вероятность
,
то по аксиоме непрерывности существует
вероятность
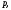 для которой
для которой
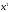 ̴
̴
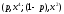 ,
,
Поэтому
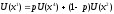 ,
или
,
или
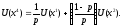 Таким
образом, после того как выбраны два
произвольных числа, полезность шкалы
фон Неймана-Моргенштерна определена.
Таким
образом, после того как выбраны два
произвольных числа, полезность шкалы
фон Неймана-Моргенштерна определена.
Важным
следствием теоремы о математическом
ожидании полезности является правило
рационального поведения в процессе
принятия решения в условиях риска.
Допустим предприниматель, принимающий
решение, должен выбрать одну из
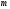 стратегий:
стратегий: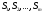 ,
где исходом стратегии
,
где исходом стратегии
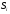 является лотерея
является лотерея
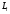
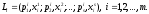
Величина
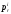 характеризует вероятность выигрыша
набора
характеризует вероятность выигрыша
набора
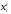 при заданной стратегии
при заданной стратегии
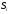 .
Полезность лотереи
.
Полезность лотереи
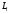 оценивается как
оценивается как
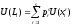 .
.
Экономический субъект, принимающий решение, чтобы максимизировать полезность, выберет стратегию, которая обеспечивает наибольшее значение ожидаемой полезности
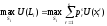 .
.
Если
имеется три возможные стратегии, для
каждой из которых заданы вероятности
выигрыша одной из двух альтернатив
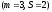 ,
то оптимальной стратегии соответствует
наибольший элемент главной диагонали
следующей матрицы:
,
то оптимальной стратегии соответствует
наибольший элемент главной диагонали
следующей матрицы:
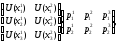
где в качестве матрицы полезностей выступает платежная матрица, а вторая матрица состоит из вероятностей.
