Плоские графы

Граф называется плоским (планарным), если его можно уложить на плоскости так, чтобы его ребра нигде не пересекались, кроме как в вершинах. Имеется два основных непланарных графа — Г5 и Г3,3, изображение которых дано на рисунке 7. Оба графа Г5 и Г3,3 являются регулярными, но последний относится еще и к так называемому двудольному, который определяется здесь как многозначное отображение трех верхних вершин на три нижние вершины, или наоборот. В общем случае в двудольном графе Г3,3 число вершин в обоих рядах может быть любым.

Рисунок 7. Плоские графы

Двудольный граф

Двудольный граф (или биграф, или чётный граф) — это граф G(V,E), такой что множество вершин V разбито на два непересекающихся подмножества V1 и V2, причём всякое ребро E инцидентно вершине из V1 и вершине из V2 (то есть соединяет вершину из V1 с вершиной из V2). То есть, правильная раскраска графа двумя цветами. Множества V1 и V2 называются «долями» двудольного графа. Двудольный граф (рисунок 8) называется «полным», если любые две вершины из V1 и V2 являются смежными. Если |V1|=a,|V2|=b , то полный двудольный граф обозначается Ka,b.

Рисунок 8. Двудольный граф

Изоморфный граф

Изоморфизм — это очень общее понятие, которое употребляется в различных разделах математики. В общих чертах его можно описать так: Пусть даны два множества с определённой структурой (группы, кольца, линейные пространства и т. п.). Биекция между ними называется изоморфизмом, если она сохраняет эту структуру. Такие множества со структурой называются изоморфными. Изоморфизм всегда задаёт отношение эквивалентности на классе таких множеств со структурой. Два графа G=(X,U) и L=(X',U') являются изоморфными, если между парами множеств их вершин, ребер и дуг существуют взаимно однозначные соответствия, сохраняющие смежность и ориентацию для дуг. Пример: следующие графы, приведенные на рисунке 9, изоморфны:

Рисунок 9. Изоморфный граф

Псевдограф

Псевдограф — граф с кратными ребрами и петлями. Пример: пусть D=(V,X) – ориентированный граф, V={V1,V2},X={x1={V1,V2},x2={V1,V2],x3={V1,V2},x4={V2,V2} . Тогда D=(V,X) – ориентированный псевдограф (Рисунок 10).

Рисунок 10. Псевдограф

Мультиграф

Мультиграф — граф, в котором имеются кратные (параллельные) ребра. Мультиграф – это псевдограф без петель. Пример: пусть D=(V,X) – ориентированный граф,V={V1,V2} ,X={x1={V1,V2},x2={V1,V2}} . Тогда D=(V,X)– ориентированный мультиграф (Рисунок 11).

Рисунок 11. Мультиграф

Простой граф

Простые графы — не имеющие петель и кратных рёбер (Рисунок 12).

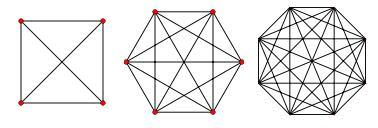
Рисунок 12. Простой граф

Полный граф

Полный граф — простой граф, в котором каждая пара различных вершин смежна. Полный граф с n вершинами имеет n(n − 1) / 2 рёбер и обозначается

Kn. Является регулярным графом степени n − 1.

2. Основные операции над графами

Рассмотрим графы и(Рисунок 13).

а) Дополнением графа называется графмножеством вершин которого является множествоа множеством его рёбер является множество

б) Объединением графов ипри условии, чтоназывается графмножеством вершин которого является множествоа множеством его рёбер является множество

в) Пересечением графов иназывается графмножеством вершин которого является множествоа множеством его рёбер является множество

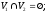
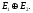г) Суммой по модулю двух графов (Рисунок 14). ипри условии, чтоназывается графмножеством вершин которого является множествоа множеством его рёбер – множествоТ. е. этот граф не имеет изолированных вершин и состоит только из рёбер, присутствующих либо в первом графе, либо во втором графе, но не в обоих графах одновременно.

Рисунок 13. Операции над графами

Рисунок 14. Сумма по модулю 2