1.3.1. Теоретико-множественные операции реляционной алгебры

Теоретико-множественные операции реляционной алгебры – это операции, привнесенные в реляционную алгебру из теории множеств.

Выделяют следующие теоретико-множественные операции:

• объединение;

• пересечение;

• разность;

• расширенное декартово произведение.

Объединением двух отношений называется отношение, содержащее множество кортежей, принадлежащих либо первому, либо второму исходному отношению, либо обоим отношениям одновременно.

Пусть заданы два отношения ,, гдеr₁ и r₂ - соответственно кортежи отношений R₁ и R₂, тогда объединение

,

где r – кортеж нового отношения; - операция логического «ИЛИ».

Рассмотрим пример данной операции.

Предположим, имеются отношения R₁ и R₂, которые содержат списки деталей, изготавливаемых соответственно на первом и втором участках цеха. Отношение R₃ содержит общий перечень деталей, изготавливаемых в цехе.

Пересечением отношений называется отношение, которое содержит множество кортежей, принадлежащих одновременно и первому и второму отношениям.

,

где r – кортеж нового отношения; - операция логического «И».

В отношении R₄ содержится перечень деталей, которые выпускаются одновременно на двух участках цеха.

Разностью отношений R₁ и R₂ называется отношение, содержащее множество кортежей, принадлежащих R₁ и не принадлежащих R₂.

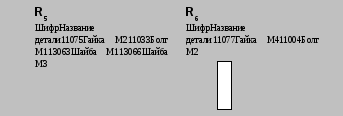
R₅ содержит перечень деталей, изготавливаемых только на участке 1, отношение R₆ – только на участке 2.

,

.

Операции объединения и пересечения являются коммутативными, т.е. результат этих операций не зависит от порядка следования аргументов в операции.

Операция разности является несимметричной, т.е. результат операции будет различным для различного порядка аргументов.

В отличие от навигационных средств манипулирования данными, в теоретико-графовых моделях операции реляционной алгебры позволяют получить качественно иной результат:

1. Операции сразу целиком выполняются на отношениях.

Для пользователя и прикладного программиста это означает, что в результате таких операций он сразу получит результат. Следовательно, пользователю не придется «вручную» последовательно перемещаться по базе данных в поисках необходимых записей, а программисту не придется писать отдельную программу для простейшей обработки данных;

2. Результатом выполнения операции является новое отношение, отражающее состояние исходного отношения в определенной части.

Расширенное декартово произведение – это операция, сходная с полным декартовым произведением множеств. В полном декартовом произведении участвуют домены, т.е. полное декартово произведение множеств – это сцепление всех возможных значений доменов друг с другом в определенном порядке. Расширенное декартово произведение – это сцепление реальных множеств, реальных наборов атрибутов отношения друг с другом.

Сцеплением или конкатенацией кортежей иназывается кортеж, полученный добавлением значений второго в конец первого. Сцепление кортежейиобозначается как.

,

где – число элементов в первом кортеже,– число элементов во втором кортеже.

Расширенным декартовым произведением отношения степени со схемой и отношения степени со схемой называется отношение степени со схемой , содержащее кортежи, полученные сцеплением каждого кортежа отношения с каждым кортежем отношения .

Т.е. если , , то

.

Операцию расширенного декартова произведения можно считать симметричной (), т.к. полученные отношения эквивалентны.

Операция расширенного декартова произведения используется для получения некоторого универсума – отношения, которое характеризует все возможные комбинации между элементами отдельных множеств.

Например, пусть существует отношение , содержащее обязательную номенклатуру деталей для всех цехов, и отношение, содержащее перечень всех цехов. Требуется получить отношение, в котором была бы отражена ситуация, когда каждый цех изготавливаетвсе детали.

Универсум не имеет самостоятельного значения, но может активно использоваться в операциях над данными. Так, операцию расширенного декартова произведения (или получения универсума) нужно использовать во всех ситуациях, которые характеризуются словом «все».

Например, нужно узнать, какие детали в каких цехах из общей обязательной номенклатуры не выпускаются (). В данном случае универсумом является общая обязательная номенклатура (). Имеется также отношение, характеризующее реальный выпуск деталей в каждом цехе. Для получения искомого результата необходимо выполнить следующую операцию:

.