инфа / Calc / Л.р. 3 OOo Calc

Лабораторная работа № 3

Решение систем линейных алгебраических уравнений матричным методом. Метод статистического моделирования – Монте-Карло.

Теоретический материал.

СЛАУ

Многие задачи экономического характера сводятся к решению систем линейных уравнений. Систему вида:

,

,

………………………………………,

принято называть системой n линейных алгебраических уравнений (СЛАУ) с n неизвестными.

При этом произвольные числа aij (i = 1, 2,…, n; j = 1, …, n) называются коэффициентами системы (коэффициентами при неизвестных), а числа bi (i = 1, 2,…, n) – свободными членами. Такая форма записи алгебраической линейной системы называется нормальной. Решением СЛАУ называется совокупность чисел xi (i = 1, 2,…, n), при подстановке которых в систему каждое из ее уравнений обращается в тождество.

Система уравнений называется невырожденной, если она имеет хотя бы одно решение (определитель не равен нулю, и вырожденной – в противном случае (определитель равен нулю).

Табличные формулы и операции с матрицами

Табличные формулы или формулы массива – очень мощное вычислительное средство ЭТ, позволяющее работать с блоками рабочего листа как с отдельными ячейками. Формулы массива в качестве результата возвращают массив значений. Поэтому перед вводом такой формулы необходимо выделить диапазон ячеек, куда будут помещены результаты. Затем набирается сама формула. Формула вводится во все ячейки выделенного интервала. При активизации любой ячейки из интервала, содержащего формулу массива, в строке формул отображается введенная формула, заключенная в фигурные скобки. Именно фигурные скобки являются признаком формулы массива. Невозможно редактировать содержимое только одной ячейки из интервала с табличной формулой. Изменить можно только весь блок целиком.

К простейшим операциям с матрицами принято относить следующие: сложение и вычитание матриц, умножение и деление матрицы на число, перемножение матриц, транспонирование, вычисление обратной матрицы. Умножение (деление) матрицы на число, сложение (вычитание) матриц в Calc реализуются просто: с помощью обычных формул (поэлементное сложение или вычитание, умножение или деление на число), либо с использованием формул массива. Для остальных матричных операций в Calc предусмотрены функции из категории математические.

•MDETERM – вычисление определителя матрицы;

•MINVERSE – вычисление обратной матрицы;

•MMULT – произведение матриц;

•INDEX – вычисление содержимого ячейки из заданного диапазона;

•ROWS – вычисляет количество строк в массиве;

•COLUMNS – вычисляет количество столбцов в массиве.

•TRANSPOSE – транспонирование матрицы.

OpenOffice.org Calc позволяет присвоить массиву ячеек (матрице) имя. Это упрощает обращение к этому массиву ячеек и делает формулы более наглядными.

Матрица в общем случае может быть заполнена не только числовой, но и текстовой информацией.

Метод Монте-Карло

Методы Монте-Карло – численные методы решения математических задач при помощи моделирования случайных величин.

Метод статистического моделирования, или метод Монте-Карло, назван так в честь столицы княжества Монако, известной своими многочисленными казино, в которых публика рассчитывает или увеличивает свои доходы согласно законам распределения случайных величин.

1

Этот метод позволяет решать задачи, в условиях которых присутствует элемент неопределенности (например, при подбрасывании монеты может выпасть "орел" или "решка"). На ЭВМ с помощью генератора (датчика) случайных чисел имитируются ситуации или процессы, приводящие к тем или иным исходам. Высокой точностью такой метод похвастаться не может, но он пользуется популярность, благодаря ясности и прозрачности метода получения результатов. Идейно метод Монте-Карло схож с методом грубой оценки, которым часто пользуются главы компаний и департаментов, чтобы проверить «точные» данные, представленные финансовыми и аналитическими службами. Точности же метода – 1-2% – для практики более чем достаточно.

Первоначально метод использовался главным образом для решения задач нейтронной физики, где традиционные численные методы были не эффективны. Далее его влияние распространилось на широкий класс прикладных задач экономики (оптимизация, управления, планирование), химии, биологии – очень разных по своему содержанию.

Сущность метода Монте-Карло состоит в следующем: производят n испытаний, в результате которых получают n возможных значений Х; вычисляют их среднее арифметическое и принимают x в качестве оценки (приближённого значения) искомого числа a.

Это вероятностная сходимость, то есть чем больше значений мы получим, тем достоверней утверждать, что результат близок к истинному. Следовательно, требуется получить множество случайных чисел.

Функции генерации случайного числа из заданного интервала:

1.Функция RAND() позволяет возвращать дробное случайное число в интервале от 0 до 1.

2.Для получения случайных чисел в другом диапазоне необходимо воспользоваться следующей формулой: RAND()* (b – a) + a, где b – верхняя граница, а – нижняя (генерация нового случайного числа происходит после каждого пересчета таблицы или нажатием клавиши F9).

3.Функция RANDBETWEEN(A, B) возвращает целое число из интервала (A, B).

Задание к работе.

Уражнение1. Решение систем линейных алгебраических уравнений средствами ЭТ. Действия над матрицами.

1.В соответствии с номером варианта выберите из приведенных ниже систему линейных алгебраических уравнений четвертого (n=4) порядка. Приведите ее к нормальному виду. Разработайте схему (шаблон приведен ниже) для решения выбранной СЛАУ матричным способом.

Порядок действий:

•Получить обратную матрицу для матрицы коэффициентов. Предварительно вычислить определитель и убедиться, что матрица невырож-

денная (функция MDETERM).

•Решить систему уравнений, перемножив обратную матрицу и матрицу

свободных членов. Решение записать в указанный блок.

•Сделать проверку полученного результата двумя способами:

•подставив значения неизвестных в исходные уравнения;

•перемножив матрицу коэффициентов и полученную матрицу неизвестных (должна получиться матрица свободных членов уравнения).

2.Продемонстрировать работу остальных функций и алгебраических операций не участвующих в вычислении.

2

3

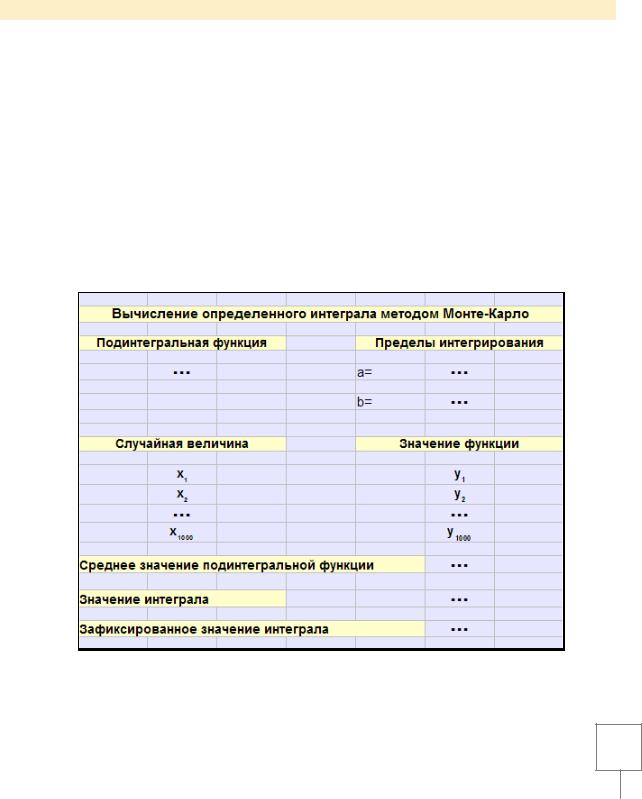
Уражнение 2. Вычисление определенных интегралов методом Монте-Карло.

1.Для более наглядного представления записать подынтегральную функцию

влинейном виде, ввести пределы интегрирования.

2.Найти 1000 случайных значений (X) из заданного диапазона (пределы

интегрирования).

3.Для найденных случайных значений (X) вычислить подынтегральные функции (Y).

4.Рассчитать Fср – среднее значение подынтегральной функции, вычисленное

в1000 случайных точек из области (функция AVERAGE()).

5.Вычислить значение интеграла по формуле: Fcр * (b – a),

6.Зафиксировать значение (Копировать → Вставить как…).

Схема вычисления по методу Монте-Карло

4

ООО CALC. Лабораторная работа №3 (OOO Calc) Информатика 2009

Варианты заданий:

Контрольные вопросы.

1.Условие существования обратной матрицы.

2.Определение значения ячейки из заданного диапазона.

3.Как присвоить имя массиву?

4.Как произвести сложение (вычитание) матриц?

5.Как произвести умножение матрицы на число?

6.Определение числа строк и столбцов.

7.Как возвратить целое случайное число из заданного интервала?

8.Продемонстрировать работу специальной вставки.

5