Ответы к теории по матану / 14. Площадь плоской фигуры

Из геометрического смысла определенного интеграла следует, что площадь криволинейной трапеции, ограниченной сверху кривой , снизу отрезком  оси , справа и слева прямыми  и  (рисунок 6), находится по формуле

. (30)

Рисунок 6 – Криволинейная трапеция	Рисунок 7 – Фигура, ограниченная линиями , ,

Если криволинейная трапеция расположена ниже оси , то есть  (рисунок 7), то площадь может быть найдена по формуле

. (31)

Площадь фигуры, ограниченной кривыми  и  ( для любого ), прямыми  и  (рисунок 8), можно найти по формуле

 . (32)

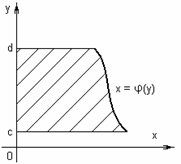
Если криволинейная трапеция ограничена справа непрерывной кривой , слева отрезком  оси , снизу и сверху прямыми   и  (рисунок 9), то ее площадь находится по формуле

. (33)

Рисунок 8 – Фигура, ограниченная линиями , ,  и	Рисунок 9 – Криволинейная трапеция, расположенная относительно оси

Если криволинейная трапеция ограничена кривой, заданной параметрическими уравнениями

,

то ее площадь находится по формуле

. (34)