
Ответы к теории по матану / 11. Интеграл с переменным верхним пределом. Формула Ньютона-лейбница
..docxТеорема о производной от интеграла с переменным верхним пределом (с доказательством).
Если
в определенном интеграле  изменять
верхний предел b,
то будет меняться и значение интеграла,
то есть интеграл будет функцией верхнего
предела.
изменять
верхний предел b,
то будет меняться и значение интеграла,
то есть интеграл будет функцией верхнего
предела.
Обозначим
верхний предел x,
а переменную интегрирования, чтобы не
смешивать ее с верхним пределом,
обозначим t.
Таким образом, интеграл с переменным
верхним пределом является функцией
от x:  .
.
Имеет
место теорема: производная
интеграла с переменным верхним пределом
от непрерывной функции равна подынтегральной
функции, в которой переменная интегрирования
заменена верхним пределом: 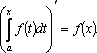
Лейбница - даёт соотношение между операциями взятия определенного интеграла и вычисления первообразной. Формула Ньютона-Лейбница - основная формула интегрального исчисления.

Данная формула верна для любой функции f(x), непрерывной на отрезке [а, b], F - первообразная для f(x). Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f(x) , вычислить ее значения в точках a и b и найти разность F(b) – F(a).
