НОВЫЕ ОТВЕТЫ / все предметы / ТЭС

Теория электрической связи.

1. Частотно-модулированный сигнал имеет девиацию частоты Δf_М=1МГц при частоте модуляции F=5кГц. Определить девиацию частоты сигнала после прохождения его через избирательный усилитель с одиночным колебательным контуром в качестве нагрузки, если добротность контура Q=100, резонансная частота которого f₀, совпадающая с несущей частотой, равна 500кГц.

Общая запись сигнала с ЧМ.

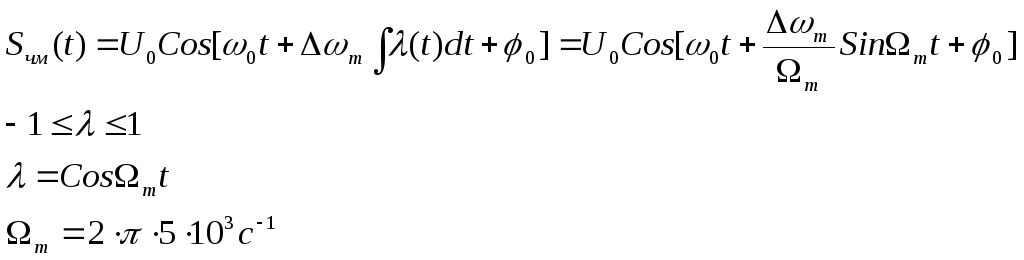
Предложенный сигнал имеет индекс модуляции , поэтому его спектральная диаграмма содержит несущую составляющую и 2 боковые с амплитудами, составляющими 0,5m=0,1 относительно амплитуды несущей.

Коэффициент передачи усилителя с колебательным контуром записывается в виде: , где ω₀ –частота несущей. Модуль коэффициента передачи находится по формуле: .

К₀ , на резонансной частоте.

-на верхней боковой частоте.

Т. к. спектральная характеристика симметрична относительно ω₀ , то на нижней боковой то же самое.

U_вых=U₀ * K₀ ; U_выхВБ =U_выхНБ =

Из полученного выражения видно, что при условии задачи модуль коэффициента передачи усилителя для боковых составляющих в раз меньше коэффициента передачи для несущей. Из этого следует, что индекс модуляции сигнала на выходе усилителя в раз меньше индекса на входе, т.е. Тогда девиация частоты выходного сигнала равна: Δf_{М МАХ}=m_ВЫХ*F=0,089*5*10³=447 Гц.

2. Пропускная способность непрерывного канала связи с помехой при F_в=10⁶ Гц и отношении мощностей сигнала и помехи q²=63 равна С=6*10⁶ бит/с. Необходимо увеличением полосы канала F_в добиться повышения пропускной способности в 2 раза не меняя мощность сигнала. Рассчитать, во сколько раз необходимо увеличить полосу сигнала и какое отношение сигнал/шум получится после повышения полосы.

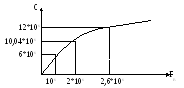- теорема Шенона; q²=; N₀- спектр плотности шума.

; ; .

3. Построить спектральную диаграмму сигнала с амплитудной модуляцией:

S(t)=U₀[1+M₁cos(₁t+₁)+M₂cos(₂t+₂)]cos[₀t+], где U₀=1В, M₁=0,8, M₂=0,2, ₁=2*10³1/с, ₂=2*3*10³1/с, ₁=/4, ₂=/2, =0, ₀=2*10⁵1/с.

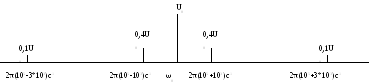
S(t)=U₀[1+M₁cos(₁t+₁)+M₂cos(₂t+₂)]cos[₀t+]= U₀cos[₀t+]+U₀M₁cos(₁t+₁)cos[₀t+]+ U₀M₂cos(₂t+₂)cos[₀t+];

Cos x*Cos y=1/2*Cos(x-y)+1/2*Cos(x+y)

S(t)= U₀cos[₀t+]+1/2U₀M₁cos(-₁t-₁+₀t+)+ 1/2U₀M₂cos(-₂t-₂+₀t+)+1/2U₀M₁cos(₁t+₁+₀t+)+ +1/2U₀M₂cos(₂t+₂+₀t+);

4. Случайный процесс с функцией корреляции К_х()=_х²ехр{-А²²/4}поступает на фильтр нижних частот с коэффициентом передачи К()=ехр{-²/2D²). Найти функцию корреляции выходного процесса.

x(t) y(t)

1. S_x(ω)=2K_x(τ)e^-jωτdτ - на входе.

2. S_y(ω)= S_x(ω) /K(jω)/² - на выходе.

3. Ky(τ)=1/4π S_y(ω) e^jωτdω - Функция корреляции.

e^-Ax2+-2Bx+Cdx= e^(B2+AC)/A;

.

Затем умножаем на квадрат модуля коэффициент передачи, т.е.

5. Сигнал S(t)=U₀e^-t, где =10³. Найти частоту дискретизации, если допустимое значение относительной среднеквадратичной ошибки  (воспроизведения) сигнала не выше 0.1%.

Эффективное значение относительной ошибки временной дискретизации сообщения определяется равенством:

где Ω_д – частота временной дискретизации;

G_S(jω) – спектральная плотность мощности сообщения S(t).

Ω_В=0,5Ω_д – гипотетическая верхняя частота спектра процесса S(t).

Находя спектральную плотность G_S(jω), имеем

Вычисляя интегралы в выражении для δ можно получить:

Используя приближенное равенство при больших значениях переменных X, можно получить:

. Тогда следовательно,

Следовательно, Ω_д=2Ω_в=2*10⁹с^-1.

5. Найти рекуррентную последовательность максимальной длины (М – последовательность), состоящую из семи импульсов, изобразить структуру согласованного фильтра для ее сжатия и форму сигнала на его выходе.

Достоинства сложных сигналов:

Сложные сигналы обладают повышенной помехоустойчивостью по отношению к помехам с сосредоточенным спектром (узкополосным помехам);

Так же сложные сигналы обладают повышенной разрешающей способностью, которая позволяет разделить сигналы при многолучевом распространении.

Кроме того, использование сложного сигнала позволяет обеспечить синхронизацию устройства восстановления аналогового сообщения по принятому цифровому сигналу.

Т.о., необходимо выбрать два вида используемых сигналов с ЧМ –частотной манипуляцией (это последовательность импульсов, у которых частота меняется специальному коду). Один сигнал должен быть использован для синхронизации, второй – для передачи информационных символов.

Существует два типа кода:

код Баркера;

М–последовательность

К-ый элемент последовательности рассчитывается по формуле:

где С и d – двоичные числа. Таблица 1

n	C1	C2	C3	C4	C5
3	1	0	1
3	0	1	1
4	0	0	1	1
4	1	0	0	1
4	0	0	1	0
5	0	1	0	0	1
5	0	1	1	1	1
5	1	1	1	0	1
5	1	0	1	1	1
5	1	1	0	1	1

– максимальный уровень лепестка.

Составим М-последовательность для информационного элемента. Для этого зададим первые три импульса:

Произвольно выберем из таблицы 1 комбинацию С, состоящую из 4 элементов

Рассчитаем остальные элементы:

Т.о., мы получили М-последовательность для информационного элемента: 1011100

Единиц должно быть больше, чем нолей на один разряд.

СФОИ – согласующий фильтр одиночного импульса.

На выходе будем иметь сигнал, амплитуда которого в 7 раз будет больше за счет задержки наших импульсов.

Один сигнал должен быть использован для синхронизации, второй – для передаци информационных символов.

Форма напряжения на выходе СФОИ.

							1
						1	1
					0	0	1
				0	0	1	1
			0	0	1	1	1
		1	1	0	0	0	1
	0	0	1	1	1	0	1
	-1	0	1	-2	-1	0	7

Нашу М-последовательность мы либо инвертируем (умножаем на «-1» нашу комбинацию), либо оставляем такой, какая есть. Чтобы узнать, нужно ли нам инвертировать или нет, у нас должны в один столбик по последнему разряду (в столбец) быть 7единиц. Подбирая нашу комбинацию, мы смотрим нужно инвертировать или нет. Затем складываем столбцы. Нули заменяются на «-1», а единицы – на «+1». Разность между «+1» и «-1» является результатом, который записывается после черты. По этим результатом строим график.

7. Прямоугольный радиоимпульс длительностью _и поступает на полосовой усилитель с одиночным резонансным контуром в качестве нагрузки. Найти значение постоянной времени контура (по отношении к длительности импульса), обеспечивающее максимальное отношение амплитуды сигнала к эффективному значению шума на выходе фильтра.

Коэффициент передачи : С помощью преобразования Фурье :

Спектральная плотность м.б. записана в виде:

Спектральная плотность огибающей сигнала видеоимпульса

Для амплитуды мы можем заменить ω₀ на Δω, т.к. сдвинули из ВЧ в НЧ огибающую:

Т_э- постоянная времени контура .

Чтобы найти закон огибающей надо пропустить радиоимпульс через цепь с - НЧ эквивалент.

Нас интересует максимум полезного сигнала на выходе RC – цепи.

В то же время дисперсия шума на выходе RC-цепи, возбуждаемой со стороны входа белым шумом, описывается выражением

, где W₀ спектральная плотность мощности белого шума.

Отсюда максимальное значение отношения сигнал/шум на выходе RC-цепи

Приняв во внимание, что энергия рассматриваемого видеоимпульса E_s=U₀²τ_и получается

Первый сомножитель отношение сигнал/шум. Второй оценивает проигрыш в отношении сигнал/шум RC-фильтра по сравнению с согласованным фильтром. Введя безразмерный параметр x=τ_и/(RC) рассмотрим функцию

Из графика видно, что при х=1.25 значение величины к(х) достигает максимума, равного 0.814. Для прямоугольног радиоимпульса длительностью τ_и можно применить полосоваой фильтр с полосой пропускания П_0.707=0.72/ τ_и.